微信(WeChat)是腾讯公司于 2011 年推出的一款移动即时通讯软件,在几年中逐步由一个沟通工具转化为移动平台。目前,微信的用户数超过 6.5 亿,月活跃用户超过 4.7 亿,微信在中国大陆的市场渗透率达 93%,海外用户数也已突破 1 亿。
微信公众平台是一个自媒体平台,它在仅在 15 个月内就增长到 200 多万个,并每天保持 8000 个的增长,呈现出超过亿次的信息交互。微信公众平台的文章可以方便地分享到微信朋友圈中。微信朋友圈是微信重要的社交功能,它已经成为了中国 Facebook 分享平台。朋友圈可以发照片和文字,也可以分享链接,而朋友圈链接分享的很大一部分来源于微信公众平台。
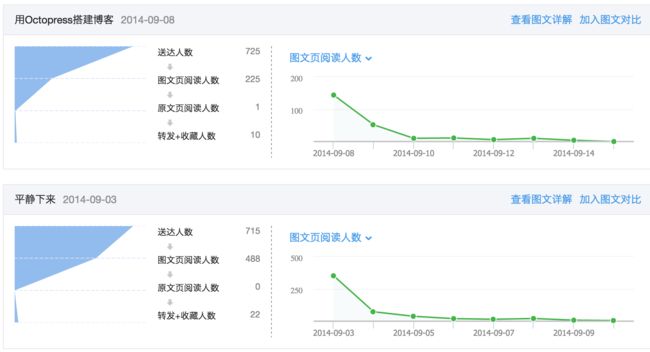
微信公众平台分为订阅号和服务号两类,订阅号允许每天群发 1 条消息。值得注意的是,微信公众平台的后台提供了包括用户分析、图文分析、消息分析等完善的统计数据,相当于 Google Analytics 的部分功能,因此微信公众平台的运营者可以通过对这些数据进行分析,优化运营结果。2013 年底,我申请开通了自己的微信公众平台订阅号 Etter(微信号:etter_ding)。一年来共群发 30 余次图文消息,获得 700 余人的关注。
很长一段时间我都在关注一个叫做「DW 月谈」的微信订阅号。「DW 月谈」的作者 DW 于 2014 年毕业于北京大学经济学专业,现就职于豌豆荚商业产品团队,她的文章十分生动有趣。前不久,我阅读了 DW 同学在她的微信公众号「DW 月谈」上发表的文章《一个分享几人看:基于DW月谈的数据分享》。这篇文章十分有趣,DW 根据她的微信号「DW 月谈」发表29篇文章的数据,做了回归分析并得出「一个分享大概 9 人看」的结论。
事实上,我一直在试图粗略估计 DW 月谈的关注量。不过我所能准确得知的唯一数据是每篇文章的阅读量(显示在每篇文章末尾)大概在两三千到六七千波动,另外我估计「DW 月谈」的阅读率会在 30%~40% 左右。(虽然对于很多公众号阅读率都可能达不到10%,但 DW 月谈的文章比较有趣,加上是个人账号推送也不算频繁,我对「DW 月谈」的阅读率估计要比常量高很多。)由此,我粗略计算出「DW月谈」的关注量大致会在 8000 至 10000 左右。不过 DW 在这篇文章中透露了真实数据:现在共有 5935 名关注者,文章的阅读率高达 53%。这个阅读率让我真的有点吃惊——我估计的还是太过保守,但是想到「DW 月谈」的确是我收到推送后几乎唯一会立即打开阅读的公众号,也能够信服。
在文章中 DW 试图找到影响单篇微信文章阅读量的因素。经过粗略的计算,DW认为文章分享量,微信号关注人数,以及文章标题劲爆程度和单篇文章的阅读量显著正相关,而文章字数、发布具体时刻、文章是否曾经发布过、文章标题字数等因素则与文章分享量不显著相关。DW 根据数据进行了一个简单的多元回归,得到了关注者数量和分享量和阅读量的关系:阅读量 = 9.04 * 分享量 + 0.53 * 关注者人数 – 157,其中阅读量和分享量 p-value < 0.01,同时通过计算了每篇文章预测值和真实值的差异,可以观察到「标题党」的阅读量显著高于预测值。DW 在文章总结到:「文章火起来的要点有三个:分享热、粉丝多、标题劲爆。」
这样的回归分析比较有说服力,不过联想到最近所学的计量经济学内容,我便沿著这个回归过程进一步思考下去。显然,DW 在该篇文章中使用了 OLS (Ordinary Least Square,普通最小平方法)进行回归分析。回顾 DW 在文章中总结到,文章阅读量与分享量、关注者人数、标题劲爆程度这三个变量显著正相关,并跑出回归方程:阅读量 = 9.04 * 分享量 + 0.53 * 关注者人数 – 157。
注意到,在这三个显著影响关注量的变量中,「标题劲爆程度」无法用数值衡量,所以被放到了误差项(error term)中。但是这样的处理是否合理呢?标题劲爆程度虽然是不可衡量变量,但是它和分享数有很大相关性,因为一般来说我们都会认为,标题比较劲爆的文章分享数也会比较多。那么如果单纯用 OLS 做回归,即将标题劲爆程度放在误差项中,是否会影响回归函数的准确性呢?
于是我在想是否可以引入工具变量(IV,Instrumental Variable)解决。根据维基百科,「在回归模型中,当解释变量与误差项存在相关性(内生性问题),使用工具变量法能够得到一致的估计量。」当一个解释变量(regressor)和误差项(error term)相互独立,并不对因变量产生影响,称为外生性(exogeneity)。与外生性相对立的是内生性(endogenous),也即误差项和解释变量存在相关性。在回归模型中,如果遇到内生性问题,使用OLS会出现不一致的估计量。那么可以使用工具变量(Instrumental Variable,简称 IV)解决这个问题。这里,工具变量应该满足: 1>和内生解释变量存在相关性;2>此变量和误差项不相关,也就是说工具变量严格外生。
接下来的问题是,在 DW 的数据中选择什么作为工具变量比较合适?我想了很久,觉得或许可以选择「关注数」作为一个较为合理的 IV。当然由于我手中没有数据,只能表示 IV 的选择并不是唯一的,只要满足所找的 IV 与分享数有关,但是和标题劲爆程度无关即可。找到合理的 IV 之后,用Two-stage Least Squares(2SLS)做回归,并用 Hausman Test 检验所选取的 IV 是否恰当。这样或许就可以得到一个更为一致的估计量了。
于是第二天,我把我自己对处理 DW 数据的一点思考写了下来。由于 DW 并不认识我,我没有想到 DW 竟然在博客看到了我的文章并留下了评论,在此谢谢她的评论:「IV是一个很好的解决思路,但是在样本有限的情况下加入IV的意义就不大了,因为IV需要很大的数据量才会显著;此外找到一个合适的IV也是个问题。」
我觉得 DW 说的也有道理,这个思路就没有继续想下去。然而,分析我自己微信公众平台运营数据的想法却日渐强烈了。我的数据更加有限,但是也不妨用最简单的方法,稍微尝试一下。
我也准备探究一下我自己的微信订阅号阅读数和什么因素有关。由于微信于 2014 年 7 月才开放「阅读次数」信息,所以该数据不完整,我于是使用「阅读人数」作为因变量。影响因变量阅读人数的因素可能有:距上次发布相距时间,文章字数,订阅号累计关注人数,以及转发人数等等。接着我耐心的统计了数据,并通过跑简单的线性回归发现:「阅读人数」与「距上次发布相距时间」、「文章字数」等因素的相关性不明显,但是与「累计关注人数」以及「转发人数」明显线性相关。
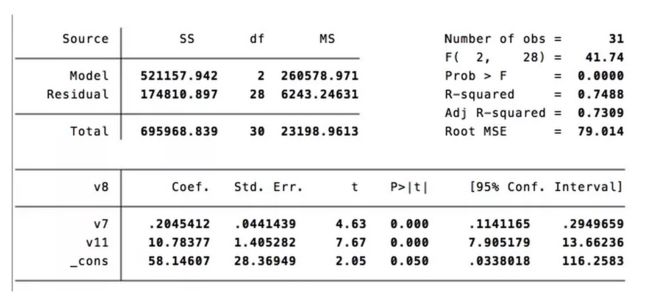
于是我对「阅读数」与「订阅号累计关注人数」以及「转发数」做了回归分析,得到数据结果:
阅读次数 = 0.205 * 订阅号累计关注人数 + 10.78 * 转发数 + 58.15
这说明,文章在朋友圈的转发 1 次,大概可以增加 10 人阅读;而关注人数增加 5 人,才能带来 1 人阅读量的增加。
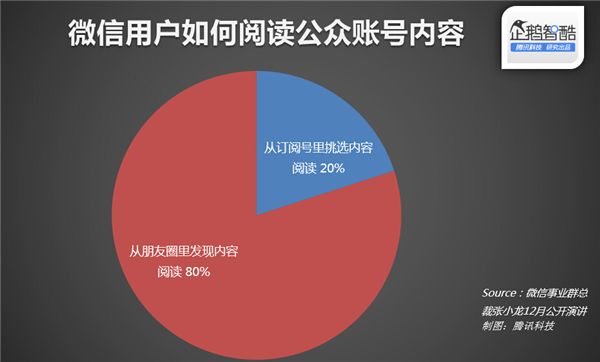
这个结果大致符合了张小龙在 12 月微信公开课上的一个数据分享。他在演讲中提到,订阅号有非常多的阅读量来自朋友圈,这符合 2/8 分布原理,「20% 的用户到订阅号里面去挑选内容,然后 80% 的用户在朋友圈去阅读这些内容」。我看到有人质疑过该论断的合理性,但是从我回归分析的数据中看,我觉得这大致是合理的。
微信订阅号有 80% 的阅读量来自朋友圈,也即朋友圈里好友转发的内容才是用户阅读的主要来源。看来,好的内容才是提高微信订阅号阅读数最重要的因素,这也提醒我如果想增加文章的阅读数,就必须写出更好的文章,并获取更多的转发。
原文链接:http://dinglisa.com/blog/2015/01/09/wechat-analysis