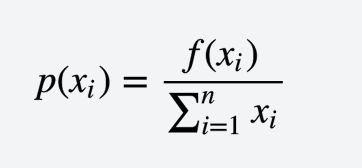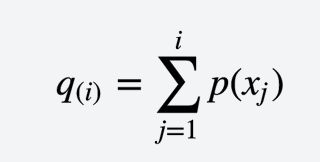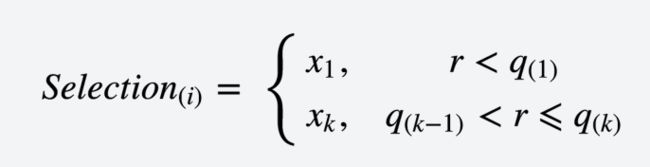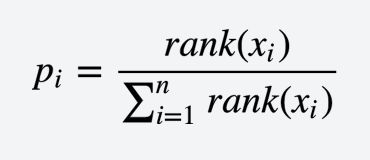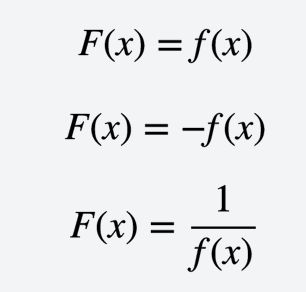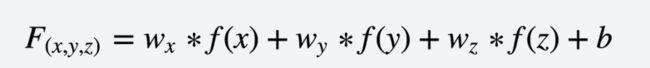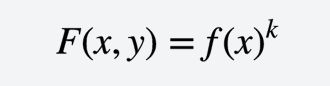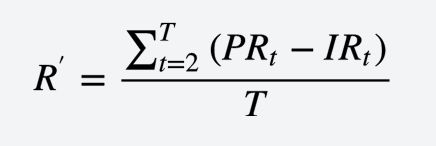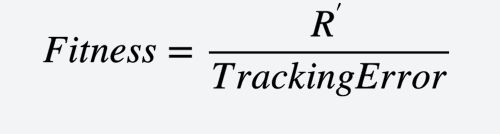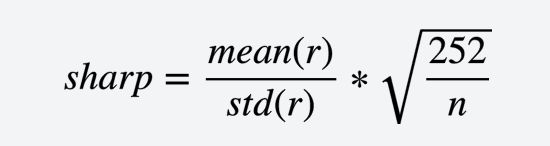遗传算法在量化投资的应用
本篇内容涉及遗传算法的概念,原理描述,实现方法以及在量化投资的应用。
作者:陈焕生,凡普金科旗下会牛科技研发总监兼数据架构师,目前从事基于遗传算法因子自动化挖掘,量化投资研究。并于2017年上线了基于遗传算法因子挖掘的自有资金运营的量化模型。目前处于行业中游水平,团队的大多背景都是非金融投资领域,实现互联网技术向量化投资领域的转型,本人十年的互联网研发背景,多次连续创业的经历。
什么是遗传算法
- 介绍遗传算法的概念
遗传算法是一种进化策略的算法,模拟生物基因遗传。遵循物竞天择,适者生存,劣者淘汰的自然规律进化。
达尔文有一句话这么说的:
能够生存下来的往往不是最强大的物种,也不是最聪明的物种,而是最能适应环境的物种
简单的说,随着时间的流逝,一代代的繁殖,不管外部的环境如何恶劣,都会通过遗传和变异生存下来,以致适应环境。不适应环境的生物将会被淘汰。
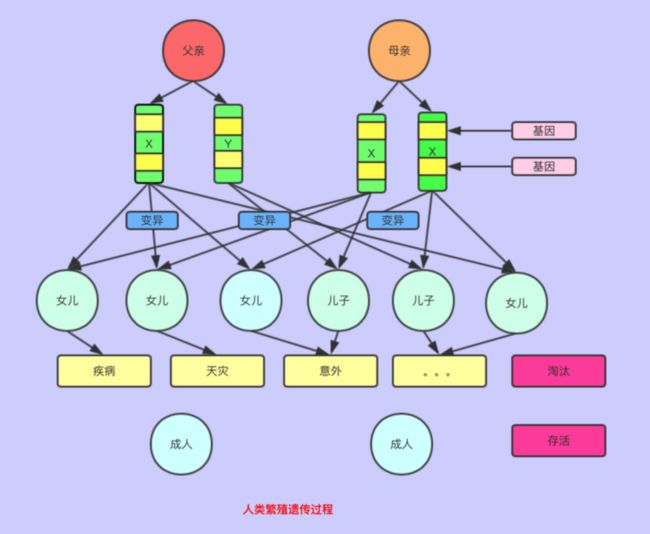
人类的进化概要图如下:
-
遗传算法的原理
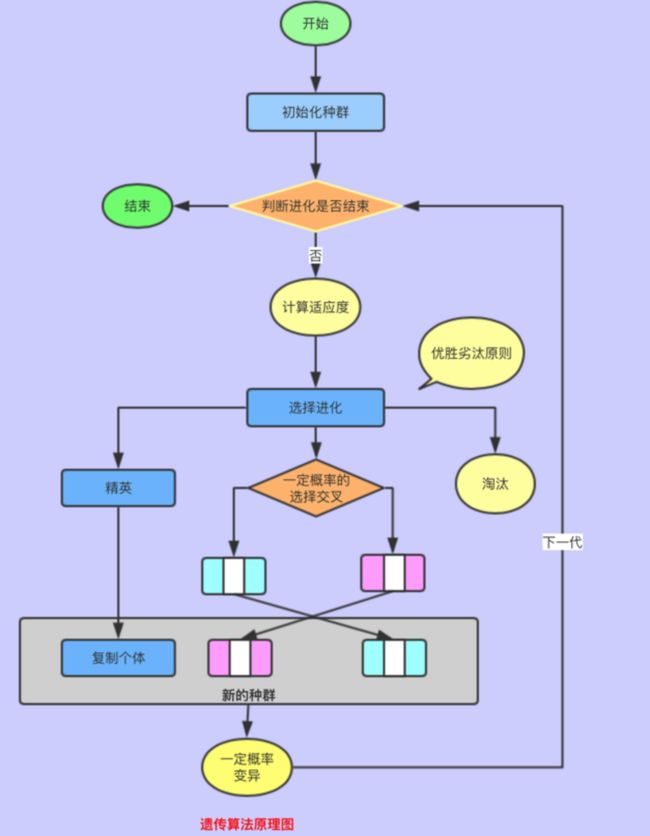
遗传算法的基本原理就是模拟上述的繁殖遗传的过程。
提炼出遗传算法的基础组件如下:
种群(Population)
生物进化是以群体的形式进行的,人类就是一个种群,种群还可以分为子种群,每个子种群分别进化
个体(Individual)
组成种群的独立单个物种
染色体(Chromosome)
包含一组基因,个体由多个染色体组成
基因(Gene)
可用于遗传的因子,并且携带特有的适应能力的信息
交叉(Crossover)
个体之间交换染色体,交叉繁殖遗传基因,形成新的个体
复制(reproduction)
复制优秀的个体,遗传基因
变异(Mutation)
根据一定概率基金突变,增强基因的多样性
进化(Evaluation)
根据优胜劣汰原则,进化优秀个体,淘汰劣类个体
遗传算法实现的方法
遗传算法实现的步骤大体分为基因编码解码,种群初始化,选择算子,交叉算子,变异算子,适应度函数(评价函数或者目标函数)。每个步骤的优化都会影响到遗传算法整体的优化结果。
基因编码
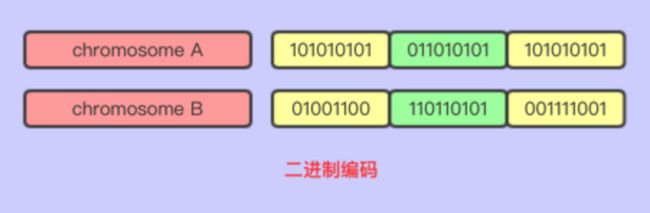
- 二进制编码
二进制编码顾名思义由二进制来编码,由0和1组成的基因编码成染色体
如右图:
适用场景:解决背包问题
详解:背包问题一般给定某些东西固定的大小和价值,背包的容量是有限的,优化最大背包价值类似的问题
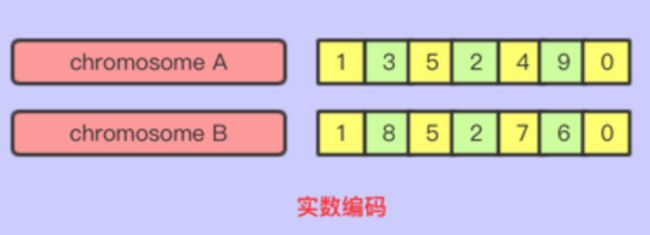
- 实数编码
实数编码是在给定的连续或者离散的区间内,将实数组合成有序的序列的一种编码
如右图:适用场景:解决排序的优化问题,例如TSP问题,任务排序,任务调度等问题
详解:这类问题对于顺序敏感,TSP问题就是路径规划的优化
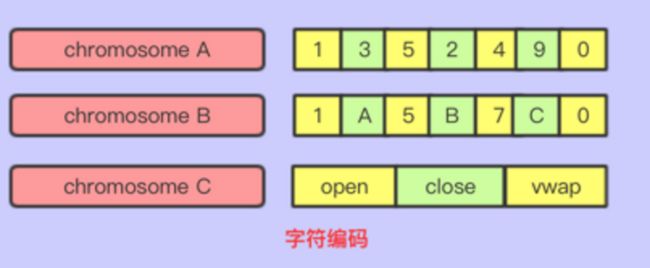
- 字符编码
实数编码其实可以认为是字符编码的一种,实数编码的基因都是实数组成的,而字符编码可以由字母,单词,数字等组成,字符编码也可以将字符通过定义固定字典表的方式,转换成实数编码。
如右图:
适用场景:优化神经网络的参数,权重等
详解:在设计好的神经网络的模型中,使用遗传算法优化权重,得到最佳的输出
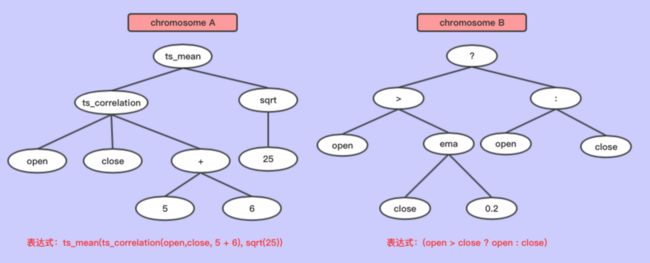
- 符号编码
一般符号编码都使用树来存储,所以符号编码也可以称为树编码,是一种复杂的编码方式。量化投资的因子挖掘编码就是采取这种方式。
适用场景:给定特征,找出一个函数,以达到目标优化的方式
详解:这种方式,每一个特征可以作为一个变量成为基因,每一个表达式就是一个染色体,对于这个染色体的交叉和变异其实就是树节点的交换和变异。
选择算子
- 轮盘赌选择算法(Roulette Wheel Selection)
每个个体进入下一代的概率和它的适应度值成正比,它的进化概率是个体的适应度占总的适应值的比例。
具体算法如下:
- 计算每个个体的适应度值$f(x_i), i = (1,2,...,n),n为种群的大小$
计算种群所有个体的进化到下一代的概率。
计算个体的积累概率。
在[0, 1]区间生成一个随机数r
- 重复(4)共N次。这样就选出来了一个新的种群。
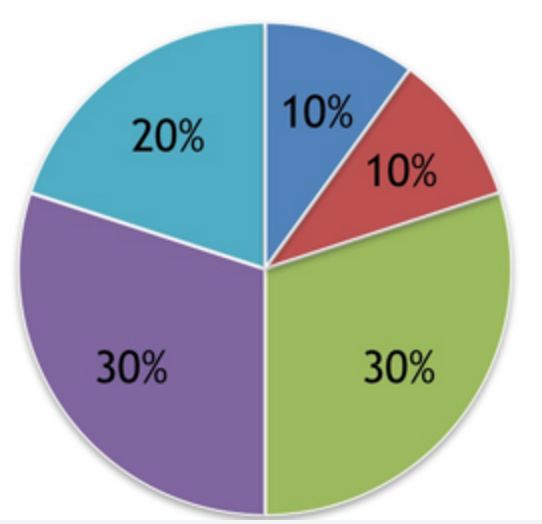
举例如下:
如同轮盘旋转一样,面积越大,落上去的概率越大
优点:选择的概率与它的适应值成正比
缺点:适应度如果差别太大,如果最好的染色体适应值占比90%,那其他的染色体的进化机会将很小,这样不利于种群进化的多样性了。
- 排名选择算法
这种选择算法就会避免上述适应度差别很大的问题。
- 精英选择算法
将种群中最好的适应度的个体直接进化到下一代,避免优秀的个体在交叉和变异的时候,丢失良好的基因。
- 其他选择算法
还有其他的扩展的选择算法,例如随机竞争选择、期望值选择,排挤策略等
交叉算子
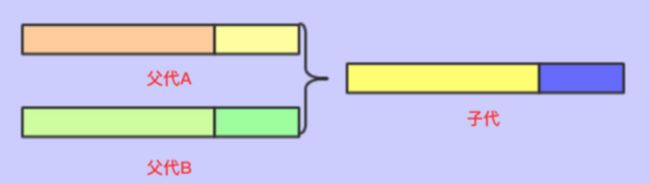
- 单点交叉
指在个体编码基因串中只随机设置一个交叉点,然后再该点相互交换两个配对个体的部分基因
如右图:
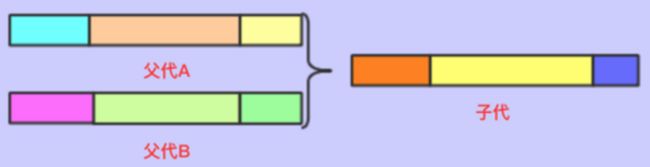
- 两点交叉
指在个体编码基因串中随机设置两个交叉点,然后再该点相互交换两个配对个体的部分基因
如右图:
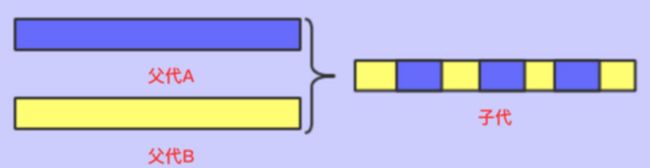
- 一致交叉
两个配对的个体在每个基因点上以相同概率交叉
如右图:
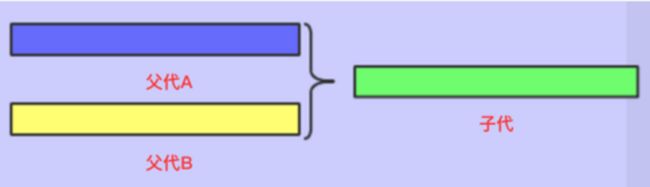
- 算术交叉
通过算术表达式计算得到新的基因,例如and,or,xor等
如右图:
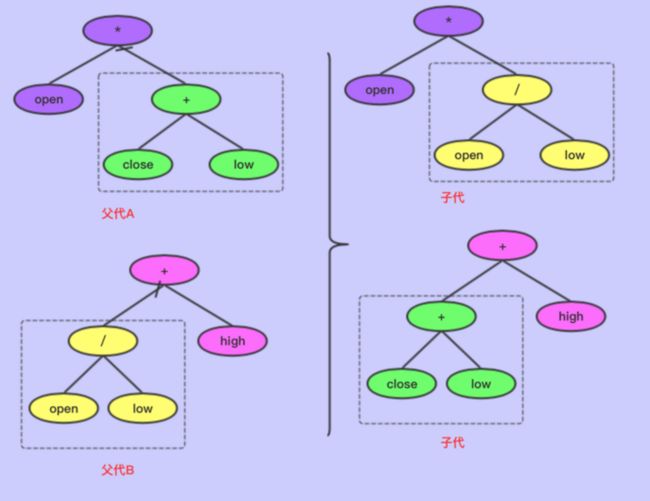
符号编码的交叉
变异算子
- 基本位变异:对个体基因编码中以变异概率、随机指定的某一位或某几位做变异。
- 均匀变异:分别用符合某一范围内均匀分布的随机数,较小的概率来替换所有基金的基因值。(特别适用于在算法的初级运行阶段)
- 边界变异:随机的取基因两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。
- 非均匀变异:对原有的基因值做一随机扰动,以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后,相当于整个解向量在解空间中作了一次轻微的变动。
- 高斯近似变异:进行变异操作时用符号均值为P的平均值,方差为P2的正态分布的一个随机数来替换原有的基因值。
以上最常用的是基本位变异,其他的变异算法需要读者自己深入研究。
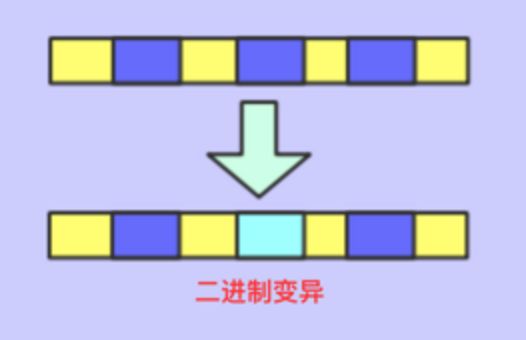
- 二进制变异
将基因进行变异即可
如右图:
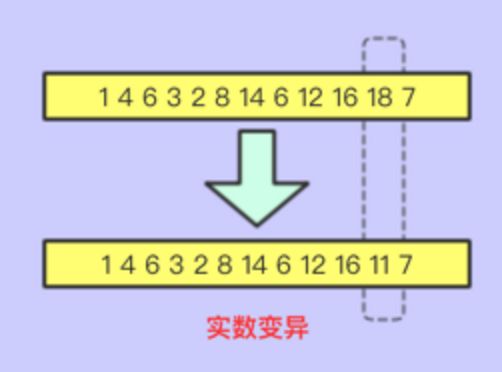
- 实数变异
将实数进行变异即可
如右图:
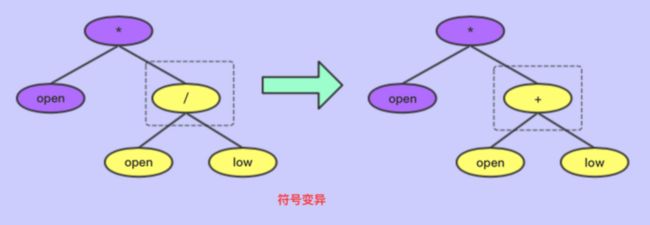
- 符号变异
将树上的节点变异,不过操作符只能变异成操作符,变量只能变异成变量
如右图:
注意:不管是交叉还是变异,都存在一定概率进行, 交叉和变异概率均是超参,不能太小,也不能他大,太大会不容易收敛到最优解,太小将容易导致种群多样性差,容易收敛。
适应度函数
适应度函数也称为评价函数,适应度函数和目标函数是两个概念,适应度函数是根据目标函数区分群体中个体的好坏的标准,适应度函数总是非负,而目标函数可能为正也可能为负。所以一般需要在两者之间进行转换。适应度函数可以理解为综合目标的一个最终评分。
适应度函数设计的要求:
- 简单分值
- 非负
- 越大越好
- 计算简单
目标函数转换适应度函数方法:
直接转换
线性转换
多个优化目标按照权重分配转换成适应度值
指数转换
遗传算法在量化投资的应用
遗传算法复制指数
在投资中,指数基金就是通过复制标的是指数的基金,一般分为完全复制,部分复制,抽象复制。例如沪深300指数,我们用沪深300的少数的成分股来复制沪深300指数。
模型分析:
- 选多少只股票(成本问题)
- 选择哪些成分股(跟踪误差问题)
- 股票权重分配(跟踪误差问题)
模型限制条件问题如下:
- 成分股的数量固定,等于M
- 成分股的持股比例有大小限制,min < x < max
目标函数定义:最后适应度函数就是:
跟踪误差 - 与指数偏离的程度
超额收益 - 组合的收益率超过指数的收益率
还可以定义为
其中w是超参,两个目标的权重。
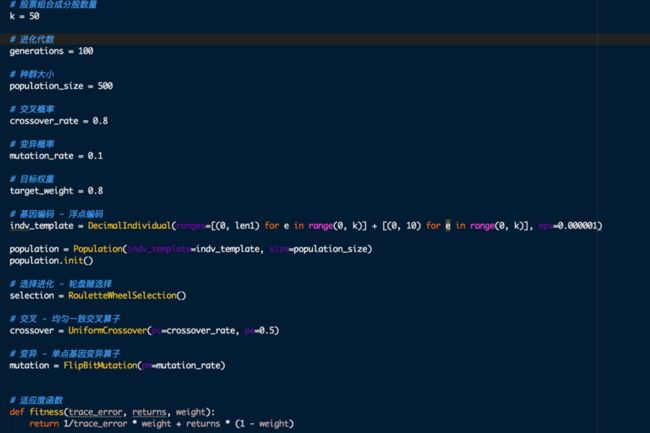
具体实现步骤参数如下:
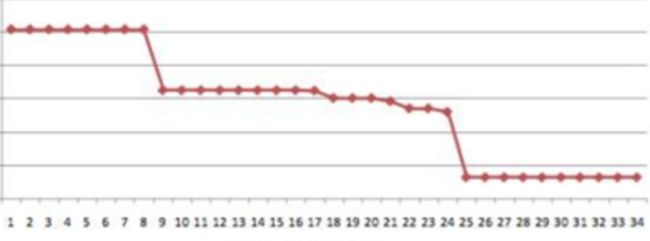
跟踪误差结果:
注意:在投资领域不是收益越高越好,而是要求收益高的同时,波动要小。一般用夏普值来衡量,在实际过程中,考虑的因素更多,比如交易手续费,停牌,st类的股票等等。
遗传算法做因子挖掘
在量化投资领域,多因子模型是量化投资的重要并且传统一个模型,因子是模型的原料,量化模型就是把不同类的因子按照一定方式组合在一起,去选股,并且预测收益。因子也可以称之为特征。在模型中你可以放入多种多样的因子,比如:动量因子,市值类因子,基本面因子,反转类因子,趋势类因子,波动因子等等。这些因子的数据来源于行情数据,高频数据,基本面数据,新闻数据,研报数据,宏观量化类,行业分析类等等。
简单因子:((close - open) / ((high - low) + .001))
复杂因子:((rank(ts_correlation(ts_sum(((high + low) / 2), 19), ts_sum(adv60, 19), 8)) < rank(ts_correlation(low, volume, 6))) * -1)
模型分析:
因子挖掘考虑因子的可交易性,目标函数最优,换手率低,泛华能力强且稳定。
- 选哪些股票参与训练
- 选定in-sample的训练时间,out-sample的样本时间
- 选定股票权重
- 选定股票收益计算周期
- 选定股票交易价格类型(open,close,vwap)
- 选定因子极值处理
基因和染色体选择:
Terminal Set:open、close、high、low、returns、volume、随机数Function Set:rank(横截面的排序)、ts_rank(时间序列排序)、correlation(横截面相关性)、ts_correlation(时间序列相关性)、decay(时间序列衰减)、decay_linear(线性衰减)、ts_mean(简单平均)、ema(加权平均)、?:(if else三元表达式) ,min,max,ts_min,ts_max
模型限制约束条件:
- 因子有效数据占比(>60%)
- 因子值数据分布
- 因子ICIR或者Sharp最低值
- 因子目标值的t-value值
目标函数定义:
`ICIR:
Sharp(夏普值):
换手率:一买一卖就是换手。换手率目标是越小越好,但是不能太小,换手才会带来收益,过高的换手会导致交易成本太高。同样也不能收益
适应度函数:
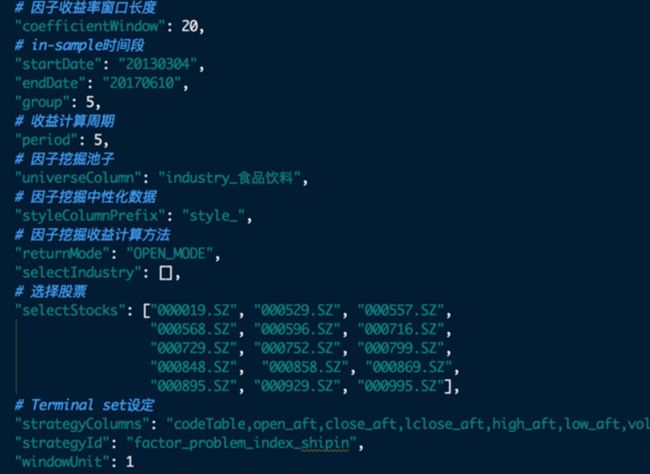
具体参数配置:
遗传算法参数配置含:
- 种群个体个数
- 子种群个数
- 随机种子
- 选择算子
- 交叉算子和交叉概率
- 变异算子和变异概率
- 适应度函数配置
- 树深度配置
- Terminal Set配置
- Function Set配置
- 其他超参配置
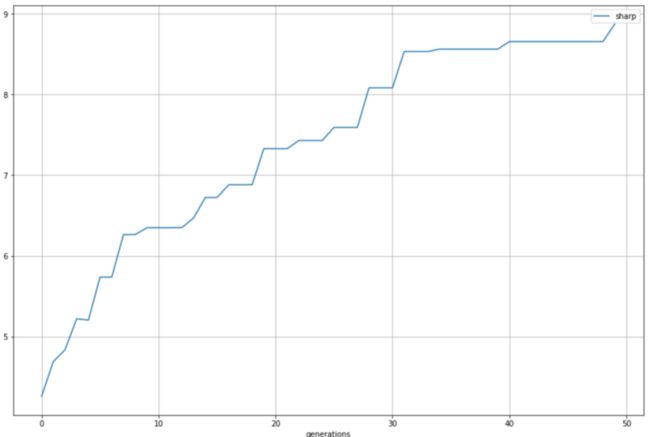
结果sharp进化图:
总结:遗传算法不仅金融领域应用广泛,还可以优化机器学习超参、机器人路径规划、流水车间调度等领域都可以应用。
遗传算法优化
- 容易局部收敛的问题
遗传算法的局部搜索很强,所以一般容易收敛用以下解决方案,具体情况具体对待。
扩大搜索空间
提高种群的数量、增加数据种类和数量、增加算子提高种群多样性
调整交叉策略、提高交叉概率、调整变异策略、提高变异概率毁灭优秀个体
对优秀个体进行存活周期倒计时,如果规定的周期内没有出现新的优秀个体,就直接杀死优秀个体,让携带有优秀基因且暂时远离目标的个体存活。
- 不容易收敛的问题
减少搜索空间
减少种群数量,减少数据种类和数量、减少复杂的算子降低种群多样性
降低交叉概率和变异概率精英策略
防止精英由于交叉变异被破坏,不能进化到下一代,对于较好的精英直接不通过交叉和变异直接进化到下一代。
- 过拟合问题
过拟合问题是在in-sample表现很好,out-sample表现非常差的问题。
样本数据
增加样本数据,让少量样本数据覆盖整体样本
模型
一开始不要使用复杂的模型,不要把所有的数据加入到模型中。
数据清洗
对于数据进行清洗,分析清洗后的数据的分布
中性化
对于相关性很高的因子可以进行中性化处理,避免朝着那个方向进化
- 多目标收敛平衡问题
单目标进化
一开始先单目标进化,收集一定的数据,分析数据分布情况
惩罚系数
对于目标拟合的时候,进行惩罚,惩罚可以根据周期进行线性,指数惩罚力度
遗传算法优缺点
- 优点:
- 基于群体的搜索,具备进化能力,不是穷举搜索
- 适应度函数简单操作
- 遗传算法很容易做分布式计算处理
- 遗传算法大大提高了搜索效率
- 遗传算法基于概率变异,具有一定随机性
- 遗传算法可以与其他算法结合,例如可以优化机器学习的超参
- 缺点:
- 遗传算法受初代随机种群影响很大,可以结合启发式算法改进
- 遗传算法的诸多参数,例如交叉率、变异率影响了搜索结果,目前大多依赖经验值
- 遗传算法利用交叉和变异产生种群,搜索速度慢
- 改进:
- 编码改进 :格雷编码、动态编码
- 选择进化:随机竞争选择,特定目标挑选
- 交叉改进:多点交叉,单点交换
- 自适应:自适应遗传算法,精英策略年龄,种群年龄
- 效率:并行计算,分布式计算
参考
- http://www.obitko.com/tutorials/genetic-algorithms/index.php
- https://en.wikipedia.org/wiki/Genetic_algorithm