【信号与系统】06 - 有理系统

1. 连续有理系统

1.1 系统函数

　　很多物理模型的系统都可以表示为式（1）的线性常微分方程，它显然是一个LIT系统。后面将会看到，这样的系统实现简单，却可以满足复杂的需求。需要注意的是，从系统角度，\(x(t),y(t)\)分别是输入、输出；但从方程角度，这里\(t\)是变量，\(x(t)\)为确定的函数，\(y(t)\)则是待求的变量。而且我们知道（回顾常微分方程），这个方程由特解\(y_0(t)\)和齐次解组成（式（2），如果\(z_0\)是\(\sum_{k=0}^n b_kz^k=0\)的\(r\)重根，那么\(e^{z_0t},te^{z_0t},\cdots,t^{r-1}e^{z_0t}\)都是齐次解）。它有无穷多组解，即可以代表无穷多个系统。

\[\sum_{k=0}^ma_kx^{(k)}(t)=\sum_{k=0}^nb_ky^{(k)}(t)\tag{1}\]

\[y(t)=y_0(t)+\sum_{i=1}^nc_ie_i(t),\;\;\sum_{k=0}^nb_ke_i^{(k)}(t)=0\tag{2}\]

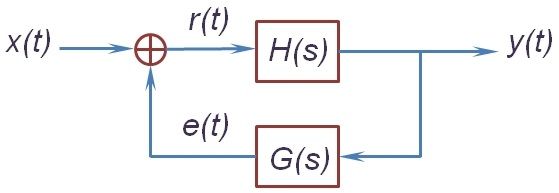
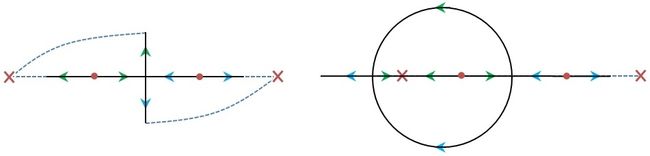
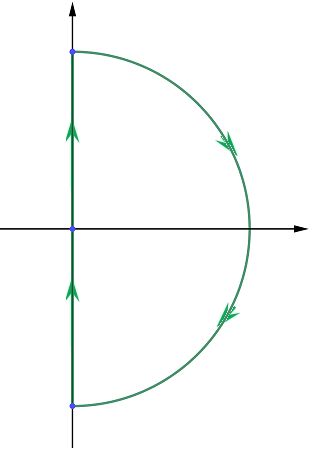
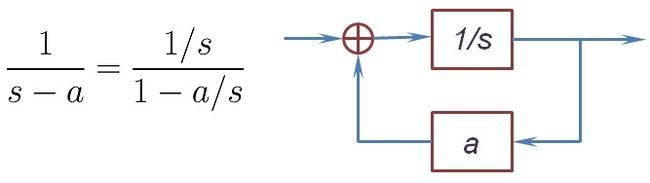
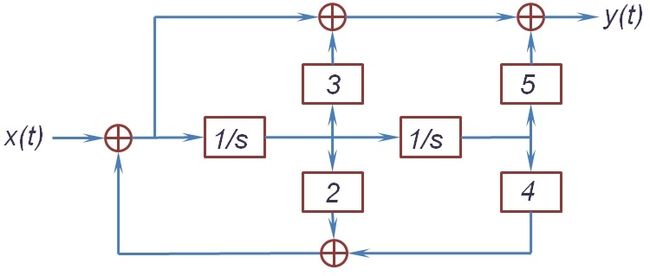
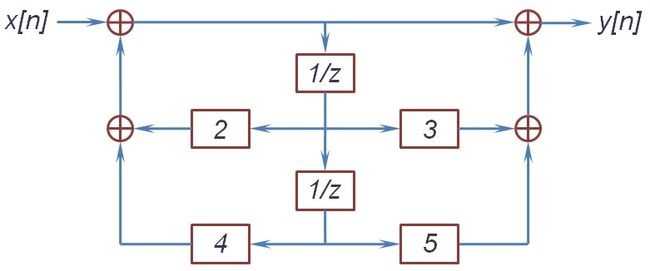
　　然而，现实中的系统往往满足初始松弛条件：如果\(t

　　时域上暂时无法分析，下面转向\(s\)域（频域），来看看系统函数\(H(s)\)。记\(x(t),y(t)\)的\(s\)域系数是\(X(s),Y(s)\)，根据微分性质计算式（1）的\(s\)域系数，整理后便有系统函数式（3），它是一个实数域的分式，这样的系统称为有理系统。我们知道，分式可以分解为一阶分式和二阶分式之和，结合ROC便能得知系统的单位冲激响应。然而在没有初始松弛的限定时，分式并不能确定唯一系统。

\[H(s)=\dfrac{Y(s)}{X(s)}=\dfrac{\sum_{k=0}^ma^ks^k}{\sum_{k=0}^nb^ks^k}\tag{3}\]

　　分式在分母为\(0\)时无意义，所以它在分母的根上一定不收敛，这些值称为分式的极点。其实，通过繁杂的论证（使用分式分解）可以知道，极点就是有理系统ROC的天然边界。特别地，因果有理系统的ROC是右平面，且以右平面为ROC的有理系统也必然是因果的。还有就是，有理因果系统稳定的充要条件是：所有极点的实部都是负数。

1.2 一阶、二阶系统

　　这里简单讨论一下一阶、二阶微分方程\(b_0y(t)+b_1y'(t)+b_2y''(t)=x(t)\)所代表的因果系统。为了简化讨论，先将系统增益缩为\(1/b_0\)使得\(y(t)\)的系数为\(1\)，再进行频域的伸缩将\(y''(t)\)或\(y'(t)\)的系数也化为\(1\)。得到的标准式如式（4）所示（只考虑稳定系统，故最高次系数为正），可以先讨论标准系统的特征，再考虑频域的缩放对原系统的影响。

\[y'(t)+y(t)=x(t);\;\;y''(t)+2\zeta y'(t)+y(t)=x(t)\tag{4}\]

　　先看一阶系统，它的频率响应为\(\dfrac{1}{1+j\omega}\)，单位冲激响应为\(e^{-t}u(t)\)。Bode图上（图见上一篇）的分贝数为\(-10\log_{10}(1+\omega^2)\)，当\(\omega\to 0\)时趋于\(0\)，当\(\omega\to\infty\)时趋于\(-20\log_{10}\omega\)。在对数尺度上它们是两条直线，相交点\(\omega=1\)称为转折频率，此处与原值有最大偏差3dB。Bode图上的相移，当\(\omega\to 0\)时趋于\(0\)，当\(\omega\to\infty\)时趋于\(-\pi/2\)，在\(\omega\in[0.1,10]\)上也有近似直线。这个例子就体现了Bode图的优势。

　　再看二阶系统，其频谱响应为\(\dfrac{1}{(j\omega)^2+2\zeta(j\omega)+1}\)，也是一个近似低通滤波，请自行讨论其Bode图的性质。\(\zeta>0\)称为阻尼系数，当\(\zeta>1\)时可以拆分为两个一阶系统之和，它称为过阻尼的。当\(\zeta<1\)时为一般的二阶系统，前面知道，它的单位冲激响应有波动和超量（含正弦函数），称为是欠阻尼的。而\(\zeta=1\)时为一阶二次系统，称为临界阻尼，它比过阻尼系统有更快的响应速度，又没有欠阻尼系统的波动和超量。

2. 离散有理系统

2.1 系统函数

　　离散信号也有类似的有理系统，它一般表示为式（5）的常系数差分方程，它也是LIT系统。这个方程的解也可以表示为特解和齐次解的线性和（式（6）），如果\(z_0\)是\(\sum_{k=0}^Nb_kz^{N-k}=0\)的\(r\)重根，则\(z_0^n,nz_0^n,\cdots,n^{r-1}z_0^n\)都是齐次解。现实中的系统还要满足初始松弛条件：如果\(n递归方程\(y[n]=\cdots\)。当\(N=0\)时方程是非递归的，这时可以直接写出单位脉冲响应（式（7），根据脉冲响应的累加性），它是一个有限脉冲响应系统（FIR）。

\[\sum_{k=0}^Ma_kx[n-k]=\sum_{k=0}^Nb_ky[n-k]\tag{5}\]

\[y[n]=y_0[n]+\sum_{i=1}^nc_ie_i[n],\;\;\sum_{k=0}^nb_ke_i[n-k]=0\tag{6}\]

\[y[n]=\sum_{k=0}^Ma_kx[n-k]\;\Rightarrow\;h[n]=a_n,\;(0\leqslant n\leqslant M)\tag{7}\]

　　接着利用LT的时移性质，不难得到系统函数为式（8），仍然可以把它看成关于\(z^{-1}\)的分式。分式的极点其实就是多项式\(\sum_{k=0}^Nb_kz^{N-k}\)的根，可以证明极点是有理系统ROC的天然边界。特别地，因果有理系统的ROC是一个圆外区域，且以圆外区域为ROC的有理系统也必然是因果的。还有有理因果系统稳定的充要条件是：所有极点都在单位圆内。这些性质都与连续系统相对应。

\[H(z)=\dfrac{Y(z)}{X(z)}=\dfrac{\sum_{k=0}^Ma_kz^{-k}}{\sum_{k=0}^Nb_kz^{-k}}\tag{8}\]

　　有了系统函数，便可以将它分解为多个一阶、二阶系统之和，也就能得到单位脉冲响应。另外根据\(\delta[n-n_0]\overset{Z}{\leftrightarrow}z^{-n_0}\)可知，如果系统函数能写成式（9）左，则可以直接写出单击脉冲响应（式（9）右）。回看式（7）便有了另外一种解释，对于其它系统函数（不限于有理系统），也可以通过泰勒级数得到式（9）左的格式。
\[H(s)=\sum_{k\in\Bbb{Z}} a_kz^{-k}\;\;\Rightarrow\;\;h[n]=a_n\tag{9}\]

2.2 一阶、二阶系统

　　现在简单讨论一下一阶、二阶差分方程所代表的系统，由于频域的缩放不同于连续系统，这里的标准式仅将\(b_0\)统一为\(1\)。一阶系统（式（10））的频率响应为\(\dfrac{1}{1-ae^{-j\omega}}\)，单位脉冲响应为\(a^nu[n]\)（只讨论稳定的因果系统），其中\(0<|a|<1\)。\(a>0\)时表现为一个低通滤波，\(a\to 1\)时往低频集中；\(a<0\)时则表现为一个高通滤波，但它有震荡和超量。

\[y[n]-ay[n-1]=x[n]\tag{10}\]

　　二阶差分有标准式（11），其中\(00\)时，系统的单位脉冲响应是式（12），它是一个欠阻尼系统，有震荡和超量（\(\theta\to\pi/2\)时震荡加剧、但过渡带变窄）。当\(\theta=0\)时，系统的单位脉冲响应是式（12）的极限，它是一个临界阻尼系统，没有震荡和超量。

\[y[n]-2r\cos\theta y[n-1]+r^2y[n-2]=x[n]\tag{11}\]

\[h[n]=\dfrac{\sin\,(n+1)\theta}{\sin\theta}r^nu[n]\tag{12}\]

3. 线性反馈系统

3.1 线性反馈系统

　　为了实现有理系统，这里需要展开讨论一下反馈系统的概念和性质，限定在LIT中也叫线性反馈系统。反馈系统可以根据之前的输出调整输入信号，以修改后续的输出结果，它有较强的纠错性和抗干扰性。典型的反馈系统如图所示，其中LIT系统\(H(s)\)和\(G(s)\)所在的分别叫正向通路和反馈通路，整个构成一个闭环系统，没有反馈通路的系统也叫开环系统。

　　根据\(R(s)=X(s)+G(s)Y(s)\)和\(Y(s)=H(s)R(s)\)，可有式（13）成立，也就是说整个闭环系统还是LIT系统，且其系统函数为\(Q(s)\)（一般假定为因果系统）。\(Q(s)\)的分式形式会为系统设计带来很大的发挥空间，这里简单举几个例子。比如式（14）是\(P(s)\)的近似逆系统；式（15）利用稳定的衰减器\(K\)得到一个稳定的放大器，其中普通放大器\(H(s)\)是不稳定的。

\[Q(s)=\dfrac{Y(s)}{X(s)}=\dfrac{H(s)}{1-G(s)H(s)}\tag{13}\]

\[\dfrac{K}{1+KP(s)}\approx\dfrac{1}{P(s)},\;\;(K\gg 1)\tag{14}\]

\[\dfrac{H(s)}{1+KH(s)}\approx\dfrac{1}{K},\;\;(|KH(s)|\gg 1)\tag{15}\]

　　反馈系统另一种广泛的应用是调节稳定性。比如一阶系统\(H(s)=\dfrac{1}{s-a}\)，加上常数反馈\(K\)便得到可调节系统\(\dfrac{1}{s-a-K}\)。二阶系统\(\dfrac{1}{s^2+as+b}\)需要同时调节一次项和常数项，也只需加上反馈\(K_1s+K_2\)，其中\(s\)是微分系统。对离散一阶系统\(\dfrac{1}{1-az^{-1}}\)，可以使用时移反馈\(Kz^{-1}\)使其变成可调节系统\(\dfrac{1}{1-(a+K)z^{-1}}\)。

3.2 稳定性判定-根轨迹法

　　稳定性在系统设计中，往往是首先要满足的，而稳定性的判定就变得尤为重要。在闭环系统中，一般会给\(H(s\)或\(G(s)\)设定一个可调系数，使得系统分母为\(1-KG(s)H(s)\)。系统稳定的充要条件是，式（16）的根不出现在虚轴及其右半平面上，这里把\(D(s)\)与\(K\)分隔开来，是为了分析过程不受\(K\)的影响。记\(D(s)\)分子、分母中较高的次数为\(N\)，则式（16）有\(N\)个根（可能有重根，对特殊\(K\)也许少于\(N\)）。另外我们有理由相信，随着\(K\)从\(-\infty\)到\(+\infty\)连续变化，这\(N\)个根的轨迹一定也是连续的。

\[D(s)=G(s)H(s)=\dfrac{1}{K}\tag{16}\]

　　观察根的轨迹、以判定系统稳定性的方法，就叫根轨迹法。对于简单的分式\(D(s)\)（次数小且只有一阶因式），其实是可以根据分式特点描述出精确的根轨迹的。首先易知，当\(K\to 0\)时根趋向于\(D(s)\)的极点，而\(K\to\infty\)时根趋向于\(D(s)\)的零点。可以想象，每一个极点、零点都是根轨迹的端点；如果把根轨迹按\(K\)的正负分为两个分支，则每个分支都起于零点而终于极点。然后易知实数轴上的每一点都在根轨迹上，而且被\(2N\)个极点、零点分隔为\(2N\)段（两个无穷大视为同一个点，重根之间视长度为\(0\)），\(D(s)\)在每一段的值正负交替（最右段为正）。

　　接下来看实轴上的分段与根轨迹分支的关系。如果分段的两端分别为极点、零点，那么这个分段一定是根轨迹的一个分支。否则分段的两端是两个分支的端点（包括重根处），这两个分支在分段上的某一点分道扬镳，进入到实轴外的复平面。而实轴之外的根轨迹一定是以实轴对称的，故两个分支走向相反的反向。当然，出走的分支终会和另一个符号相同、端点互异的分支衔接，极点、零点的成对性可以保证这一点。至于实轴外根轨迹的形状，我无力做深入讨论，除了二次式的结论比较好证明：如果有两个外出点（自行计算），它们之间的半圆弧就是根轨迹；如果一个点是无穷，根轨迹就是一条垂直平分线。

3.3 稳定性判定-Nyquist判据

　　根轨迹法只能适用于简单的分式，而且难以将轨迹与具体的\(K\)值相对应。如果有计算机辅助，对具体的\(K\)值，是可以求解式（6）的根的。但这个方法又缺少对动态的\(K\)的讨论，而本段介绍的奈奎斯特（Nyquist）判据就可以跟踪\(K\)值做稳定性判断（需要计算机辅助）。

　　先来复习一下复变分式\(D(s)\)的性质，它的辐角是所有分子因式\(s-\alpha_i\)的辐角和、减去所有分母因式\(s-\beta_j\)的辐角和。当\(s\)沿某个闭环（单环）顺时针绕转一周时，对不在闭环内的极点、零点，因式的辐角恢复原值；但对在闭环内的极点、零点，因式的辐角分别增加、减少了\(2\pi\)；而对闭环上的点则比较复杂，需要单独讨论、或事先排除这种情况。复变函数的辐角变化\(2\pi\)的整数倍，虽然不影响函数值，但在连续性讨论中（值的轨迹、微分）至关重要。设闭环内有\(P\)个零点、\(Q\)个极点，可知\(D(s)\)辐角总共减少了\(2(P-Q)\pi\)，即值的轨迹绕原点顺时针旋转了\(P-Q\)圈。

　　有了这个结论，下面继续讨论式\(1-KD(s)\)或\(F(s)=D(s)-1/K\)的零点分布。这里不考虑\(K=0\)的特殊情况，以及要求\(D(s)\)分母的阶不小于分子的阶，这样\(F(s)\)的零点都是有穷的（极点就是\(D(s)\)的极点，也是有穷的）。构造一个如图所示的闭环，当直径足够大后，它能包含右半平面所有的极点\(N_p^+\)和零点\(N_0^+\)。而直径趋于无穷时，圆弧上趋于定值，\(F(s)\)的轨迹长度在这里也趋于\(0\)，所以\(F(s)\)轨迹最终等价于\(F(j\omega)\)的轨迹。

　　借助计算机画出\(D(j\omega)\)的轨迹，它绕\((1/K,0)\)顺时针旋转的次数\(N_c\)，其实就是\(F(j\omega)\)绕原点顺时针旋转的次数。如果\((1/K,0)\)在\(D(j\omega)\)的轨迹上，说明\(F(j\omega)\)在虚轴有零点，系统不稳定。否则有关系式\(N_c=N_0^+-N_p^+\)，系统稳定的充要条件是\(N_0^+=0\)即\(N_c=-N_p^+\)，描述成\(D(j\omega)\)的轨迹绕\((1/K,0)\)逆时针旋转的次数，应当等于右半平面的极点数。顺便说一句，\(N_c\)当然也能表示左半平面零点极点的关系，但由于总的零点极点数相等，其实并不会有新鲜的结论。

　　可以看到，把\(D(s)\)和\(K\)分割开来，可以跟踪动态\(K\)对系统稳定性的影响，而且\(D(j\omega)\)与\((1/K,0)\)的距离也能表示系统允许的波动范围，这个距离称为系统的稳定性裕度。还有至于离散系统，把虚轴映射成单位圆，即有系统稳定的充要条件是：\(D(e^{j\omega})\)在\(\omega\in[0,2\pi]\)上的轨迹绕\((1/K,0)\)逆时针旋转的次数，应当等于单位圆外的极点数。

3.4 有理系统的框图

　　有理系统不仅功能强大，而且实现简单，本节使用框图来表示有理系统。首先，理论上任何分式都可以分解为简单分式（多项式）的和或者积，只要先构造出简单有理系统，通过级联、并联总可以构造出任何有理系统的框图。然而实际使用中，还要考虑器件的可靠程度和复用程度，比如微分器就没有积分器简易稳定。为了说明问题，先从最简单的一阶分式系统\(1/(s-a)\)讨论起。结合反馈系统的式（13）、以及尽量使用积分器\(1/s\)，可设\(H(s)=1/s,\;G(s)=a\)。

　　这个框图还有另外一种解释，为此来看系统的微分方程\(y'(t)-ay(t)=x(t)\)，并改写成\(x(t)+ay(t)=y'(t)\)。\(ay(t)\)是\(y(t)\)放大后的反馈，且与\(x(t)\)合并后做为正向通路的输入。再看正向通路输入\(y'(t)\)、输出\(y(t)\)，\(H(s)\)自然应当是积分器\(1/s\)。这种视角可以扩展到任何分式\(\dfrac{1}{f(s)},\;f(s)=s^n-a_1s^{n-1}-\cdots-a_n\)，正向通路上是\(n\)个积分器，第\(k\)个积分器的输出放大\(a_k\)倍后反馈到输入信号。

　　对于一般分式\(\dfrac{g(s)}{f(s)}\)，只需看成两个系统级联\(\dfrac{1}{f(s)}\cdot g(s)\)。其中多项式\(g(s)\)可直接由微分器和放大器组成，然而利用微分器和积分器的互相抵消，可直接从\(\dfrac{1}{f(s)}\)的积分器后引出所需信号。图示是分式\(\dfrac{s^2+3s+5}{s^2-2s-4}\)的系统框图，这样的图称为直接型框图。

　　最后来看离散系统，所有的分析都很类似，但还是要注意方程不同带来的框图差异。比如分式\(\dfrac{1}{1-az^{-1}}\)所代表的系统\(y[n]-ay[n-1]=x[n]\)，输出\(y[n]\)移位放大后的\(ay[n-1]\)，反馈给\(x[n]\)后又直接输出为\(y[n]\) 。这将导致离散系统直接型框图的一些差异，图示为分式\(\dfrac{1+3z^{-1}+5z^{-2}}{1-2z^{-1}-4z^{-2}}\)的系统框图（\(z^{-1}\)为移位操作），与差分方程的对应关系还是很直观的。