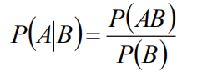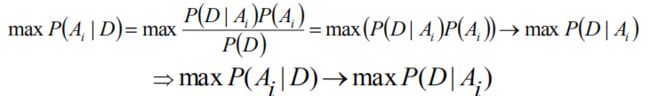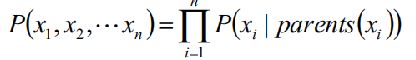知识储备
相互熵
信息增益(互信息)
条件概率:
全概率公式:
贝叶斯公式:
思考问题:
给定一个样本D,计算样本A1, A2, ...An发生的概率哪一个可能是会是最正确的呢?又怎样通过贝叶斯来解决这个问题?
通过贝叶斯公式 选择n个样本中概率最大的那个作为最后的结论。p(D)是常数,假定p(Ai)的发生概率近似相等。则有一下推导公式
贝叶斯应用实例:
一、
二、假定有两个信封,第一个信封中装有两个黑球两个红球和一美元,第二个信封中装有一个红球两个黑球,现在要求选择到存在一美元的信封的概率。
给定信息:允许随机的从一个信封中取出一个球查看他的颜色,那么此时是否应该选择该信封。
分析:c1,c2分别表示两个信封,P(R),P(B)分别表示红球的概率和黑球的概率。
全概率公式:P(R) = P(R|c1)*P(c1) + P(R|c2)*P(c2)
P(R|c1) = 2/4、P(R|c2) = 1/3、P(c1) = P(c2) = 1/2
贝叶斯求解:给定信息中看到的是红球 则选中存在一美元的信封的概率为 0.6
给定信息中看到的是黑球 则选中存在一美元的信封的概率为 3/7
贝叶斯网络:
又名 有向的无环图,是一种概率图。
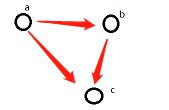
一个简单的贝叶斯网络:p(a, b, c) = p(c|a,b)p(b|a)p(a) 图形表示如下,表示的概念:a 和b是条件不独立,(a,b) 和c 也是条件不独立的。
若干个结点:最多边为C2k个有向线段(全连接,)
但是一般全连接是不建议的,也是我们不希望得到的,因为所有的边都保留着,以为这模型比较复杂
一般正常的贝叶斯网络模型
对实际贝叶斯网路的分析
注:0,1表示的是一个事件发生与不发生的概率,例如:smoking 吸烟 代表1 概率为0.3 , no smoking 代表 0 概率为则为 0.7。 这就是两个参数
贝叶斯网络:警报示例
提示:全部随机变量的联合概率分布
下图中表示 陌生人或者地震警报响起时 john 或者 mary通知的概率。
现在求 john和mary都通知铃声响起,但是没有陌生人和地震发生的概率,b-,e- 代表没有陌生人和地震的概率
p(j,m,a,b-,e-) = p(j|a)p(m|a)p(a|b-,e-)p(b-)p(e-)
= 0.9 * 0.7 * 0.001 * 0.998 *0.999
≈ 0.00063