图论基础知识(2)-三种存图法

Markdown真是不知道比TinyMCE高到哪里去

前言

如果我们要用电脑去处理一幅图的化，首先我们得想办法把这副图给存储起来。存图并不是像存数字那么简单开几个变量就能实现的，存图一般来讲有3种方法，它们分别是

1. 邻接矩阵
2. 邻接表
3. 链式前向星

那么我们先从最容易理解的邻接矩阵来看吧

邻接矩阵

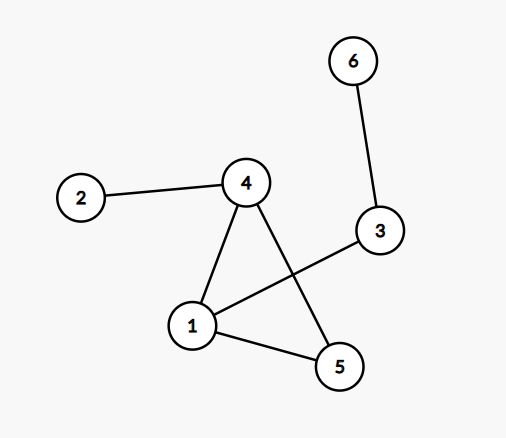
邻接矩阵的思想是在矩阵中存储每一条边的起点和终点来达到存储一幅图的目的，可以看下面的这幅图

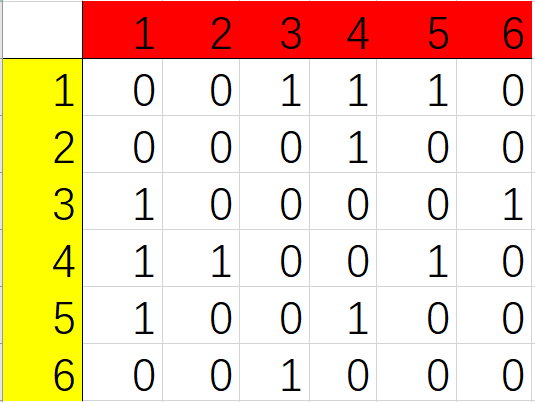
这幅图里面一共有6个点，所以我们创建一个6*6的0矩阵，并且对于每一条边，我们找出它的起点和终点，并且在矩阵的[x][y]处的0改成1.

上面这幅图在邻接矩阵里面应该这么表示：

打个比方，可以观察这幅图，我们发现对于一条连接着4和5的边，矩阵里面的(4,5)和(5,4)位置上的0都变成了1，这就是邻接矩阵的存图方法，对于图中的任意一条连接着u和v的边，我们在矩阵里面的(u,v)位置打一个标记，表示有一条边是从u到v的，同时，因为原图是一个无向图，所以对于每一组(u,v)，它们在矩阵上的(v,u)位置也要标记。如果对于有向图来说就没必要了

顺便说一句，一般在比赛里面我们输入一个图的形式都是这样的：

6 6 （表示这幅图一共有6个点和6条边）
1 4
1 3
1 5
2 4
4 5
3 6
所以在写程序的时候要注意一下。

邻接矩阵的弊端

虽然说邻接矩阵非常容易理解，但是它也有很大的缺陷：邻接矩阵消耗的空间太大了。如果我们存储一个稀疏图(|E|远小于|V|^2)，那么我们的矩阵实际上大部分都是0，也就是说我们占用了过多的空间。实际上，邻接矩阵在数学方面是一种很好的存图方式，但是设计到计算机的时候就需要考虑时间和空间，所以邻接矩阵在我们实际写程序的时候还是少用

下面给出邻接矩阵的代码：(还是非常简单的)

#include 
using namespace std;
const int maxn=1926;
int n,m,g[maxn][maxn];
int main(void){
    scanf("%d %d",&n,&m);
    for(int i=1;i<=m;i++){
        int u,v;
        scanf("%d %d",&u,&v);
        g[u][v]=g[v][u]=1;
    }
    for(int i=1;i<=n;i++){
        printf("%d: ",i);
        for(int j=1;j<=n;j++){
            if(g[i][j]) printf("%d ",j);
        }
        printf("\n");
    }
} 

邻接表

既然邻接矩阵被我们淘汰了，我们就需要找一个可以替代邻接矩阵的东西，它就是邻接表
我们可以从上面的代码里面发现，就算我们一个点u只邻接了1条边，我们的程序还是得扫描g[u][1~n]，因为我们一个点对应着它和n个点之间的信息。那么，如果我们只存储边的信息不久好了吗？邻接表就这么诞生出来了
个人认为比起语言叙述，画一个图更能体现出邻接表的思想

还是这幅图：

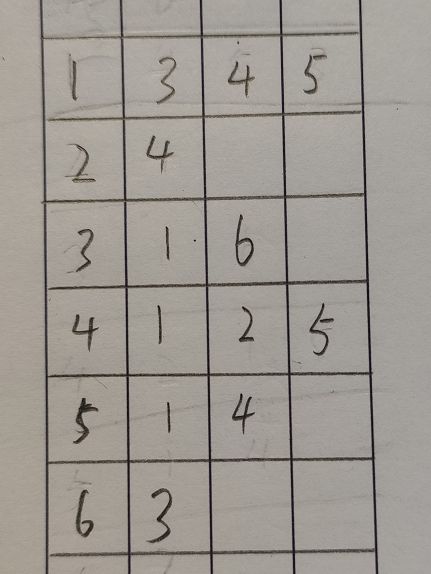
他的邻接表长这样：

（字丑所以画了好几遍)

我们可以从表里面发现，我们不再是单纯的存储0和1了，因为邻接表存储的是边。就上图来说，第一列存储的是1~N个点的编号，然后我们再看第一行，1后面的3，4，5意思是和1相邻接的第一条边的终点是3，和1相邻接的第二条边的终点是4，和1相邻接的第三条边的终点是5。这样的化我们的空间就节省了许多，同时访问的速度也快了许多。

可以试一试这道题：
https://www.luogu.com.cn/problem/P3916
非常基础的图论练手题（比打着普及-的标签还要你套最短路的水题不知道高到哪里去），个人觉得很适合练手
代码：

#include 
using namespace std;
const int maxn=100010;
struct edge{
    int to;
    edge(int to_){
        to=to_;
    }
};
vector gpe[maxn];
int ans[maxn],m,n;
void dfs(int u,int d){
    if(ans[u]) return;
    ans[u]=max(ans[u],d);
    for(int i=0;i=1;i--) dfs(i,i);
    for(int i=1;i<=n;i++){
        printf("%d ",ans[i]); 
    }
}

AC记录：

链式前向星

我个人很少用到链式前向星这种方法，但是周围的dalao都在用，也许这就是我和dalao们的差距吧(
emmm...链式前向星其实和邻接表差不多，但是由于我们在写邻接表的时候经常用到vector, 有些dalao写的stl源码剖析中写了，vector会先开2倍空间，并且还由于每个人的写法不同，有些邻接表的写法会导致效率上略逊于链式前向星，但是我目前还没遇到卡邻接表的题目。。。

链式前向星有2个组成部分，edge数组和head数组
edge[i]里面有to,w,next三个变量。to存储的是这条边的终点，w存储的是边权，next存储的是在edge数组里面，此时u所邻接的下一条边的下标(好绕人。。。)，然后head[u]数组存储了对于某一个点u，它在edge数组里面的下标
所以我们可以根据以上的描述写出链式前向星的代码：

#include 
using namespace std;
const int N=1e4+5;
int head[N];
int cnt=0;
struct node{
    int from;
    int to;
    int w;
}edge[N];
void add(int u,int v,int w){
    edge[cnt].w=w;
    edge[cnt].to=v;
    edge[cnt].from=head[u];
    head[u]=cnt++;
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    memset(head,0,sizeof(head));
    while(m--){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
    }
    int start;
    scanf("%d",&start);
    for(int i=head[start];i!=0;i=edge[i].from){
        cout<"<

总结

可能是因为我太蒻了，所以链式前向星这部分我讲的不是很清晰，感兴趣的化可以在网上自行搜索相关知识。。。
建图方面还有一些其他的知识(比如说网络流中如何建反边)还没提到，这只是一些比较基本的知识。
如果只是单纯考察建图，我只找到了那一道。。。