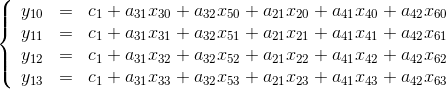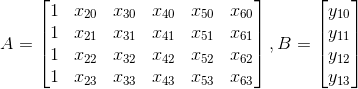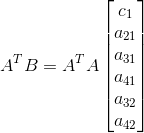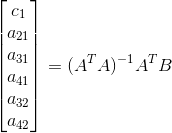东北大学 2017 年大学生数学建模竞赛 A 题一等奖成果。
在 GitHub 上:https://github.com/lalxyy/NEU-2017-MCM-A
由于不能显示行内公式,部分 LaTeX 公式以原形式展现。
摘要
东京时间 2011 年 3 ⽉ 11 ⽇ 14 时 46 分,⽇本东北地⽅太平洋海域发⽣⾥⽒ 9.0 级地震,并伴随有 7.0 到 7.4 级的多次强余震。9.0 级地震也造成了历史记录以来罕见的⾼达 39 ⽶的巨⼤海啸。截⽌到 2011 年 5 ⽉,超过 2.4 万⼈被官⽅报告为死亡或失踪;另外,福岛第⼀核电站因此发⽣的严重核事故也导致了千余⼈的⾮直接死亡,这些⼀并发⽣的重⼤事故也给⽇本及周边国家带来了严重的损失。本⽂通过评估磐城、仙台、宫古与横须贺的地震破坏及损失情况,利⽤多元线性回归的⽅式,建⽴了灾害有关因素(地震强度、海啸等)与灾害造成的后果(⼈员伤亡、经济损失)的模型。
本⽂根据互联⽹中能够查得的数据进⾏提取,并获得了沿岸海浪最⼤⾼度、与震中距离、地震⾥⽒烈度、经济⽔平(GDP)等数据,以及⼈员伤亡、财产损失的数据。根据绘制的散点图确定多元拟合中每个分量对应的多项式次数,之后将⾼次单项式换元转化为⼀次单项式,使⽤多元线性拟合来得出多项式系数。利⽤所得出的模型,本⽂又简要分析了仙台市的灾情情况,并且指出数据点较少带来的模型的不⾜之处。
关键词: 多项式拟合; 地震破坏性评估; 东⽇本⼤地震
1 问题背景与分析
1.1 背景
2011 年 3 ⽉ 11 ⽇⽇本福岛发⽣⾥⽒ 9.0 级⼤地震,强震引发海啸,导致当时全球最⼤的在役核电站——福岛核电站放射性物质外泄。该事故根据国际核事件分级被评为最⾼级 7 级,与切尔诺贝利核电站泄漏事故等级相同。截⾄ 2014 年 2 ⽉,“3.11”东⽇本⼤地震和⼤海啸死亡的⼈数达到 15884 ⼈。 截⾄ 2014 年 5 ⽉,受东⽇本⼤地震和福岛第⼀核电站事故影响,⾮直接死亡的⼈数已经达到 1699 ⼈,超过了在事故中直接死亡的 1603 ⼈。
建⽴数学模型,在以下⽇本沿海城市:磐城、仙台、宫古和横须贺 中。⽐较各种规模⼤⼩的地震破坏以及所造成的后果,并为当地报纸准备⼀篇⽂章,解释根据你的模型关于其中⼀个城市的发现。
1.2 问题分析
该问题本质为求解⼀个地震因⼦向量 x = (x_1 , x_2 , ..., x_m) 到影响程度向量 y = (y_1 , y_2 , ..., y_n) 的函数 F(可能包含多个线性变换),表示为
,怎样得出 F(x) 也是本⽂讨论的核⼼内容。
由于灾害产⽣的影响与⼈类⽣产⼒⽔平的发展情况和⼈⾃⾝的主观能动性有很⼤的关联,所以单纯凭借历史以来的地震伤亡⼈数、财产损失情况不能作为衡量当今灾害情况与财产损失的直接依据,但是⼈类⾃⾝因素又是衡量地震带来的破坏性的必要考虑因素,且关系极其复杂。为了简化模型、提⾼模型准确性与说服⼒,我们将磐城、仙台、宫古和横须贺四个地区在同⼀时间横向对⽐,不需控制时间的变量,⽽是通过与震中的距离来衡量地震的影响规模。
题⽬所给出的四个地区的建设、经济发展⽔平不尽相同。图 1 是 Google Maps 的数据,给出了四城的地理位置与震中坐标,最右侧海域中的是本次地震的震中,其余点从上到下依次为宫古、仙台、磐城、横须贺;
以及四城 2010 年当时的国民⽣产总值(GDP)[1][2][3][4]:
| 城市 | 国民生产总值 |
|---|---|
| 仙台 | 61.7 |
| 横须贺 | 12.2882 |
| 磐城 | 16.5905 |
| 宫古 | 5.19 |
表 1: 2010 年四城国民⽣产总值(单位:亿美元)
由此我们将经济因素(代表抗灾、救灾⽔平)纳⼊到考虑因素中。除此之外,根据常识,地震破坏性本⾝又与震中位置、震源深度以及城市与震中的距离相关,也是模型中必要的考虑因素。Google Maps 分别提供了四城市中⼼到震中的直线距离(表 2);
| 城市 | 与震中距离 / km |
|---|---|
| 宫古 | 186.45 |
| 仙台 | 176.75 |
| 磐城 | 207.31 |
| 横须贺 | 423.28 |
表 2: 震中直线距离
此外,连带因素还包括由于⽇本部分区域近海⽽产⽣的由地震引发的海啸影响、以及福岛核电站放射性物质外泄造成的事故。四个城市的海啸浪⾼度最⼤值可以在⽓象数据中查得 [5][6](表 3); 以及从各城市与所属县政府查得的⼈员伤亡与财产损失情况(表 4)[7][8][9][10]。
| 城市 | 海啸沿岸最⼤⾼度 / ⽶ |
|---|---|
| 宫古 | 8.5 |
| 仙台 | 8.6 |
| 磐城 | 6.51 |
| 横须贺 | 2.06 |
表 3: 观测到的海啸⾼度
注:部分观测点不以城市命名,选取对应最近的观测点。
| 城市 | 伤亡⼈数 | 经济损失(亿美元) |
|---|---|---|
| 宫古 | 611 | 22.4775 |
| 仙台 | 904 | 119.0022 |
| 横须贺 | 0 | 0.92 |
| 磐城 | 466 | 0.1478 |
表 4: 四城伤亡⼈数与经济损失
注:横须贺市政府没有说明有任何⼈员伤亡情况(参考⽂献 10),拟合过程中暂计为 0。(附录 B.2)
2 模型假设与说明
2.1 符号说明
| 符号 | 代表意义与说明 |
|---|---|
| A_1 | 仙台市 |
| A_2 | 横须贺市 |
| A_3 | 宫古市 |
| A_4 | 磐城市 |
| X | 表示地震整体因素的向量 |
| x_1, ..., x_m | 影响地震破坏性的各个因素 |
| Y | 表示地震破坏性结果的向量 |
| y_1, ..., y_n | 地震破坏程度的不同衡量特征(财产损失等) |
| F | 最终求解的地震破坏性衡量函数 |
| d_1, ..., d_4 | 对应 A_1 , ..., A_4 到震中的直线距离,单位为千⽶ |
表 5: 本⽂所使⽤的符号说明
2.2 模型假设
假设 1:⽇本本⼟海岸线在地震中没有⼤规模(超过 10 ⽶的显著)偏移;[11]
假设 2:⼈类的能动性(主观性与⽣产⼒)与发展时间相关且满⾜映射关系;
假设 3:⼈类在地震中的抗灾防灾⽔平与经济发展程度正相关;
假设 4:⼀个城市区域内的建筑物强度可以⽤⼀个平均值来表示,且可以⽤建筑物的强度、破坏程度作为衡量城市破坏程度的主要因素。
3 模型建立
3.1 知识背景
3.1.1 地震影响场
采⽤的地震烈度影响场衰减公式:
沿长轴⽅向,
沿短轴⽅向,
其中 d 表示城市与震中的直线距离。[12]
3.1.2 海啸等级
采⽤太平洋地区普遍适⽤的今村-饭⽥强度分级来评定海啸的强度等级,其中 H_av 表示沿最近海岸的平均海啸⾼度,I 为输出强度值。[13]
3.2 具体问题参数引入
由问题分析所述,已经基本可以确定 X、Y 各分量的表⽰含义。将 x_1 , x_2 , y_1 , ... 等分量指派为表 6、7 中所示的含义;四城中每个城市都与且仅与⼀组向量对应。
| 维度 | 表示含义与单位说明 |
|---|---|
| x_1 | 地震震级(⾥⽒) |
| x_2 | 国民⽣产总值(亿美元) |
| x_3 | 输⼊值在 d_1 , ..., d_4 范围内,与震中直线距离(千⽶) |
| x_4 | 海啸沿岸最⼤⾼度(⽶) |
表 6: 地震影响因⼦向量 x 各分量表示含义
| 维度 | 表示含义与单位说明 |
|---|---|
| y_1 | 伤亡⼈数 |
| y_2 | 经济损失(亿美元) |
表 7: 影响结果 y 各分量表示含义
并通过 Python 语⾔与 Matplotlib 库绘制 y 各分量与 x 各分量散点图:
3.3 基本模型
根据现有散点图及统计回归模型,认为 y_1 , y_2 为被解释变量,x_1 , ..., x_4 为解释变量。观察散点图,认为 y_1 与 x_3 ,y_2 与 x_3 满⾜⼆次多项式拟合的图像特征,且函数对应单调递减:
其中 a_{ij}, b_{ij} 为需要求出的多项式系数, i = 1, 2, 3, 4, j = 0, 1, 2,而且拟合曲线应当单调递减。类似方法可得 y_1 与 x_2、 y_2 与 x_2 线性关系,
以及 y_1 与 x_4, y_2 与 x_4 的图像特征也可用二次多项式来拟合:
y_1 与 y_2 的取值受到以上因素的影响。所以可以得出关于 x_2, x_3, x_4 的两个三元多项式拟合函数
,其中 c_1,c_2 为该多项式拟合模型中的常数,也就是
4 模型求解
引⼊拟合⽅法中的最⼩⼆乘法,使⽤多元线性回归的⽅法求解该模型。令
,此时原函数变为五元线性拟合。
对于任意一个取值点 (x_{ij}, y_{kj}),其中 j = 0, ..., 3,i = 1, ..., 6,k = 1, 2(已知四个城市对应的数据点),有
,对于 y_1,也就是
此时令
,就有
两侧同时左乘 A^T,得
,整理得
,求出 c_1, a_{21}, a_{31}, a_{41}, a_{32}, a_{42}。
使用计算机求出的最后结果为
5 模型评价与改进
该模型可以根据已有的⾃然灾害数据较为准确地求得财产损失与⼈员伤亡的程度,能够给出范围内的合理值,可⽤于防灾减灾与灾害造成后果的快速估计与判断。然⽽本模型利⽤的数据点较少,如果使⽤⼤量的数据来进⾏拟合则会使模型更有说服⼒。
6 推广与应用:仙台市
仙台市是⽇本东北地⽅的区域中⼼,也是本题⽬已知条件中离震中最为接近的城市。从之前绘制的图像和模型预估的情况来看,仙台的情况并不容乐观:常识上讲,⼀个发达区域的经济发展⽔平越⾼,防灾减灾能⼒也应该越强,这也是本⽂在模型建⽴时考虑 GDP(国民⽣产总值)作为防灾减灾因素的原因;但是由此看来,仙台及⽇本东北地⽅城市仍然需要加强对于防灾减灾⽽采取的措施,例如削弱海啸因素带来的影响,可以体现在本模型中的拟合曲线更为平滑,⽽且海啸是导致此次地震及连带事故中⼈员伤亡与财产损失的⼀个主要的原因。
参考文献
[1] 宮古市役所. 平成 23 年度 財政状況資料集 [EB/OL]. 2011. http://www.city.miyako.iwate.jp/data/open/cnt/3/5677/1/H23zaiseijoukyou.pdf.
[2] 横須賀市. 財政⽩書(平成 23 年度決算)[EB/OL]. 2012. http://www.city.yokosuka.kanagawa.jp/1610/finas/documents/hakusyo23.pdf.
[3] KANEMOTO Y. Metropolitan Employment Area (MEA) Data[EB/OL]. 2011. http://www.csis.u-tokyo.ac.jp/UEA/uea_data_e.htm.
[4] いわき市役所. 平成 23 年度決算 [EB/OL]. 2012. http://www.city.iwaki.lg.jp/www/contents/1001000003486/simple/H23_kessann.pdf.
[5] ⽇本気象庁. 国内の津波観測施設で観測された津波の観測値 [EB/OL]. 2011. http://www.data.jma.go.jp/svd/eqev/data/2011_03_11_tohoku/tsunami_jp.pdf.
[6] ⽇本気象庁. 気象庁|津波観測点(東北地⽅)[EB/OL]. 2017. http://www.data.jma.go.jp/svd/eqev/data/tsunamimap/.
[7] 宮古市役所. The Great East Japan Earthquake and Tsunami Records of Miyako City[EB/OL]. 2015. http://www.city.miyako.iwate.jp/data/open/cnt/3/5971/1/records_of_miyako_city. pdf.
[8] 仙台市役所. 東⽇本⼤震災における本市の被害状況等 [EB/OL]. 2017. https://www.city.sendai.jp/okyutaisaku/shise/daishinsai/higai.html.
[9] いわき市役所. いわき市災害対策本部週報 [EB/OL]. 2015. http://www.city.iwaki.lg.jp/www/contents/1449132951986/simple/higai0524.pdf.
[10] 横須賀市. 東⽇本⼤震災関連情報 [EB/OL]. 2011. http://www.city.yokosuka.kanagawa.jp/shinsai311/index.html.
[11] NASA. Japan’s Coastline Before and After the Tsunami[EB/OL]. 2011. https://www.nasa.gov/multimedia/imagegallery/image_feature_1893.html.
[12] 傅再扬, 危福泉, 林岩钊. 福建地震灾害损失计算分析与思考 [J]. 灾害学, 2007, 22(1) : 90 – 93.
[13] PAPADOPOULOS G A, IMAMURA F. A proposal for a new tsunami intensity scale[C] // ITS 2001 proceedings. 2001 : 569 – 577.
附录
A 程序源码
带有运⾏结果的源码与部分互动界⾯可以通过 Jupyter Notebook 打开根⽂件夹中的 /j-note ⽂件 夹内的 ipynb ⽂件来查看。
以下代码均为 Python 语⾔(Python 3)。
import numpy as np
import matplotlib.pyplot as plt
import sklearn.linear_model
import sklearn.preprocessing
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimSun'] # 在其他机器上可能需要修改字体名
mpl.rcParams['axes.unicode_minus'] = False
mpl.rcParams['savefig.dpi'] = 108
A.1 数据引入
# GDP、震中直线距离、沿岸海浪高度、震级
# x2, x3, x4, x1
miyako_x = np.array([5.19, 186.45, 8.5, 9.0]) # 宫古
iwaki_x = np.array([16.5905, 207.31, 6.51, 9.0]) # 磐城
yokosuka_x = np.array([12.2882, 423.28, 2.06, 9.0]) # 横须贺
sendai_x = np.array([61.7, 176.75, 8.6, 9.0]) # 仙台
matrix_x = np.array([miyako_x, iwaki_x, yokosuka_x, sendai_x])
# 人员伤亡、财产损失
miyako_y = np.array([611, 22,4775])
iwaki_y = np.array([466, 0.1478])
yokosuka_y = np.array([0, 0.92])
sendai_y = np.array([904, 119.9022])
matrix_y = np.array([miyako_y, iwaki_y, yokosuka_y, sendai_y])
A.2 散点图绘制
def draw_scatter_pic(x, y, description, x_label, y_label):
"""
绘制散点图的(统一方式)函数
"""
fig = plt.figure(dpi=600)
ax1 = fig.add_subplot(111)
ax1.set_title(description)
plt.xlabel(x_label)
plt.ylabel(y_label)
ax1.scatter(x, y, c = 'r', marker = 'o')
# plt.legend('x1')
plt.show()
# x_gdp = np.array([miyako_x[0], iwaki_x[0], yokosuka_x[0], sendai_x[0]])
x_gdp = matrix_x[:, 0:1]
y_person = np.array([miyako_y[0], iwaki_y[0], yokosuka_y[0], sendai_y[0]])
draw_scatter_pic(x_gdp, y_person, '散点图:人员伤亡与 GDP', 'GDP', '人员伤亡')
x_distance = np.array([miyako_x[1], iwaki_x[1], yokosuka_x[1], sendai_x[1]])
# fig = plt.figure(dpi=600)
# ax1 = fig.add_subplot(111)
# ax1.set_title('散点图:震中直线距离与伤亡人数')
# plt.xlabel('直线距离')
# plt.ylabel('人员伤亡')
# ax1.scatter(x_distance, y_person, c='r', marker='o')
# plt.show()
draw_scatter_pic(x_distance, y_person, '散点图:震中直线距离与伤亡人数', '直线距离', '人员伤亡')
x_tsunami_height = np.array([miyako_x[2], iwaki_x[2], yokosuka_x[2], sendai_x[2]])
fig = plt.figure(dpi=600)
ax1 = fig.add_subplot(111)
ax1.set_title('散点图:沿岸海浪高度与伤亡人数')
plt.xlabel('海浪高度')
plt.ylabel('人员伤亡')
ax1.scatter(x_tsunami_height, y_person, c='r', marker='o')
plt.show()
y_loss_economy = y_person = np.array([miyako_y[1], iwaki_y[1], yokosuka_y[1], sendai_y[1]])
draw_scatter_pic(x_gdp, y_loss_economy, '散点图:GDP 与经济损失', 'GDP', '经济损失')
draw_scatter_pic(x_distance, y_loss_economy, '散点图:震中直线距离与经济损失', '直线距离', '经济损失')
draw_scatter_pic(x_tsunami_height, y_loss_economy, '散点图:沿岸海浪高度与经济损失', '海浪高度', '经济损失')
miyako_x_extended = np.array([1, miyako_x[0], miyako_x[1], miyako_x[2], miyako_x[1] * miyako_x[1], miyako_x[2] * miyako_x[2]])
iwaki_x_extended = np.array([1, iwaki_x[0], iwaki_x[1], iwaki_x[2], iwaki_x[1] * iwaki_x[1], iwaki_x[2] * iwaki_x[2]])
yokosuka_x_extended = np.array([1, yokosuka_x[0], yokosuka_x[1], yokosuka_x[2], yokosuka_x[1] * yokosuka_x[1], yokosuka_x[2] * yokosuka_x[2]])
sendai_x_extended = np.array([1, sendai_x[0], sendai_x[1], sendai_x[2], sendai_x[1] * sendai_x[1], sendai_x[2] * sendai_x[2]])
np_x = np.array([miyako_x_extended, iwaki_x_extended, yokosuka_x_extended, sendai_x_extended])
np_y = np.array([miyako_y[0], iwaki_y[0], yokosuka_y[0], sendai_y[0]])
A = np.matmul(np.linalg.inv(np.matmul(np.transpose(np_x), np_x)), np.matmul(np.transpose(np_x), np_y))
print(A)
np_y = np.array([miyako_y[1], iwaki_y[1], yokosuka_y[1], sendai_y[1]])
B = np.matmul(np.linalg.inv(np.matmul(np.transpose(np_x), np_x)), np.matmul(np.transpose(np_x), np_y))
print(B)
B 关于数据及其来源的说明
本⽂使⽤的所有数据均来源于各城市政府官⽹或其他学者分析报告,在参考⽂献中都已经注明。然⽽数据中还有⼀些不够准确之处:
B.1 概念理解
很多数据载体(⽹页、报表等)只提供⽇⽂版,故依据机器翻译,数据理解上可能存在部分出⼊。
有些城市不提供 GDP 的精确数据,只提供了总收⼊、总⽀出。模型中的这部分数据根据国际通⾏的 GDP 计算⽅式计算得出。
B.2 横须贺市
横须贺市政府没有说明有任何⼈员伤亡情况(参考⽂献 10),拟合过程中暂计为 0。
B.3 仙台市
仙台市的⼀些灾难结果数据(⼈员伤亡、财产损失)⽐较违背常理,在第六节针对仙台的分析中已提及。