问题描述
所谓“马踏棋盘”问题,就是指在中国象棋的棋盘上,用马的走法走遍整个棋盘,在8*8的方格中,每个格都要遍历,且只能遍历一次。
问题解析
从起始点开始,根据“马”的走法,它的下一步的可选择数是有0—8个的。
我们知道,当下一步的可选择数为0的时候,进行回溯。当下一步的可选择数有1个的时候,我们直接取那一步就行了。但是如果下一步的可选择数有多个的时候呢? (思路取自九茶dalao)
但是我们选择下一步的时候(假设有a、b、c、d四个点可以选择),怎样选才算是最优呢?
答案是:哪一个点的下一步少,就选哪一个。
我们选择a、b、c、d之中的某一个点作为下一步,选哪个比较好,就看哪个点的后续下一步比较少。例如:马走到a点后的下一步有3个选择;而b的下一步有2个;c有1个,d有2个。那么我们的最优选择是:c点!
为什么要这样选呢?网上的解释是:“选择最难走的路,才能走的远”呜。。。好像太抽象了。
我的理解是:有些选择的后续下一步很少,例如c点,如果不先遍历它的话以后可能会很难遍历到它。
甚至极端一点的情况是,如果现在不遍历它,以后都遍历不到了。遍历不成功的时候只能回溯,一直回溯到此刻的点,然后选了c点以后才能完成,这就浪费了大量的时间。
代码实现(以前的递归代码和现在的贪心算法)
递归;
#include
#include
#include
#define X 5 //定义棋盘。为测试方便,用5格棋盘。8格棋盘的时间复杂度,真的伤不起啊……期待更好的算法
#define Y 5
void print_chess();
int next(int *x, int *y, int step);
int traverse(int x, int y, int count);
int traverse_chess(int x, int y, int tag);
int chess[X][Y]; //棋盘
int main()
{
clock_t start, end; //记录一下程序耗时
int i, j;
//初始化棋盘
for (i = 0; i < X; i++)
{
for (j = 0; j < Y; j++)
{
chess[i][j] = 0;
}
}
start = clock();
//方法一
chess[2][0] = 1;
int result = traverse(2, 0, 2);
//方法二
//int result=traverse_chess(2,0,1); //也可以使用这个方法
end = clock();
if (1 == result)
{
printf("ok\n");
print_chess();
printf("共耗时:%f\n", (double)(end - start) / CLOCKS_PER_SEC);
}
else
{
printf("此路不通,马儿无法踏遍所有棋格!\n");
}
return 0;
}
/*
判断下一个结点位置是否可用
当前结点位置(x,y)
step:下一个结点位置编号
*/
int next(int *x, int *y, int step)
{
// printf("%d\n",step);
switch (step)
{
case 0:
if (*y + 2 <= Y - 1 && *x - 1 >= 0 && chess[*x - 1][*y + 2] == 0)
{
*y += 2;
*x -= 1;
return 1;
}
break;
case 1:
if (*y + 2 <= Y - 1 && *x + 1 <= X - 1 && chess[*x + 1][*y + 2] == 0)
{
*y += 2;
*x += 1;
return 1;
}
break;
case 2:
if (*y + 1 <= Y - 1 && *x + 2 <= X - 1 && chess[*x + 2][*y + 1] == 0)
{
*y += 1;
*x += 2;
return 1;
}
break;
case 3:
if (*y - 1 >= 0 && *x + 2 <= X - 1 && chess[*x + 2][*y - 1] == 0)
{
*y -= 1;
*x += 2;
return 1;
}
break;
case 4:
if (*y - 2 >= 0 && *x + 1 <= X - 1 && chess[*x + 1][*y - 2] == 0)
{
*y -= 2;
*x += 1;
return 1;
}
break;
case 5:
if (*y - 2 >= 0 && *x - 1 >= 0 && chess[*x - 1][*y - 2] == 0)
{
*y -= 2;
*x -= 1;
return 1;
}
break;
case 6:
if (*y - 1 >= 0 && *x - 2 >= 0 && chess[*x - 2][*y - 1] == 0)
{
*y -= 1;
*x -= 2;
return 1;
}
break;
case 7:
if (*y + 1 <= Y - 1 && *x - 2 >= 0 && chess[*x - 2][*y + 1] == 0)
{
*y += 1;
*x -= 2;
return 1;
}
break;
default:
break;
}
return 0;
}
/*
遍历整个棋盘-方法一
(x,y)为坐标位置
count为遍历次数
*/
int traverse(int x, int y, int count)
{
int x1 = x, y1 = y; //新节点位置
if (count > X*Y) //已全部遍历且可用,则返回。
return 1;
int flag, result, i;
for (i = 0; i < 8; i++)
{
flag = next(&x1, &y1, i); //寻找下一个可用位置
if (1 == flag)
{
chess[x1][y1] = count; //新找到的结点标识可用,
result = traverse(x1, y1, count + 1); //以新节点为根据,再次递归下一个可用结点
if (result) //当前棋盘已全部可用
{
return 1;
}
else //新找到的结点无下一个可用位置,进行回溯
{
chess[x1][y1] = 0;
x1 = x; //结点位置也要回溯
y1 = y;
}
}
}
return 0;
}
/*
遍历整个棋盘-方法二
(x,y)为坐标位置
tag为遍历次数
*/
int traverse_chess(int x, int y, int tag)
{
int x1 = x, y1 = y, flag = 0, count = 0;
chess[x][y] = tag;
if (X*Y == tag)
{
return 1;
}
flag = next(&x1, &y1, count);
while (0 == flag && count <= 7)
{
count++;
flag = next(&x1, &y1, count);
}
while (flag)
{
if (traverse_chess(x1, y1, tag + 1)) //如果全部遍历完毕,则返回。
{
return 1;
}
//没有找到下一个可用结点,则回溯
x1 = x;
y1 = y;
count++;
flag = next(&x1, &y1, count);
while (0 == flag && count <= 7)
{
count++;
flag = next(&x1, &y1, count);
}
}
if (flag == 0)
{
chess[x][y] = 0;
}
return 0;
}
/*
打印棋盘
*/
void print_chess()
{
int i, j;
for (i = 0; i < X; i++)
{
for (j = 0; j < Y; j++)
{
printf("%d\t", chess[i][j]);
}
printf("\n");
}
} 贪心优化算法:
#include
using namespace std;
#define H 3
int next_[8][2] = { {-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2},{-2,-1}};
int f[8] = { -15,-6,10,17,15,6,-10,-17 };//把8×8的棋盘转成一维数组,马走法的八个方向分别是下标-15,-6,10,17,15,6,-10,-17
int dep = 1;//深度
int count_, z, zz; // count_ 表示目标要多少种解法,而 z 记录当前算出了多少种解法,zz 记录在运算中回溯的次数
int print[10001][8][8], F[8], a[64];//print[][][] 记录所有的遍历路径,a[] 用一维数组记录 8*8 棋盘中马的遍历路径
int Prepare() {
int i, j, n;
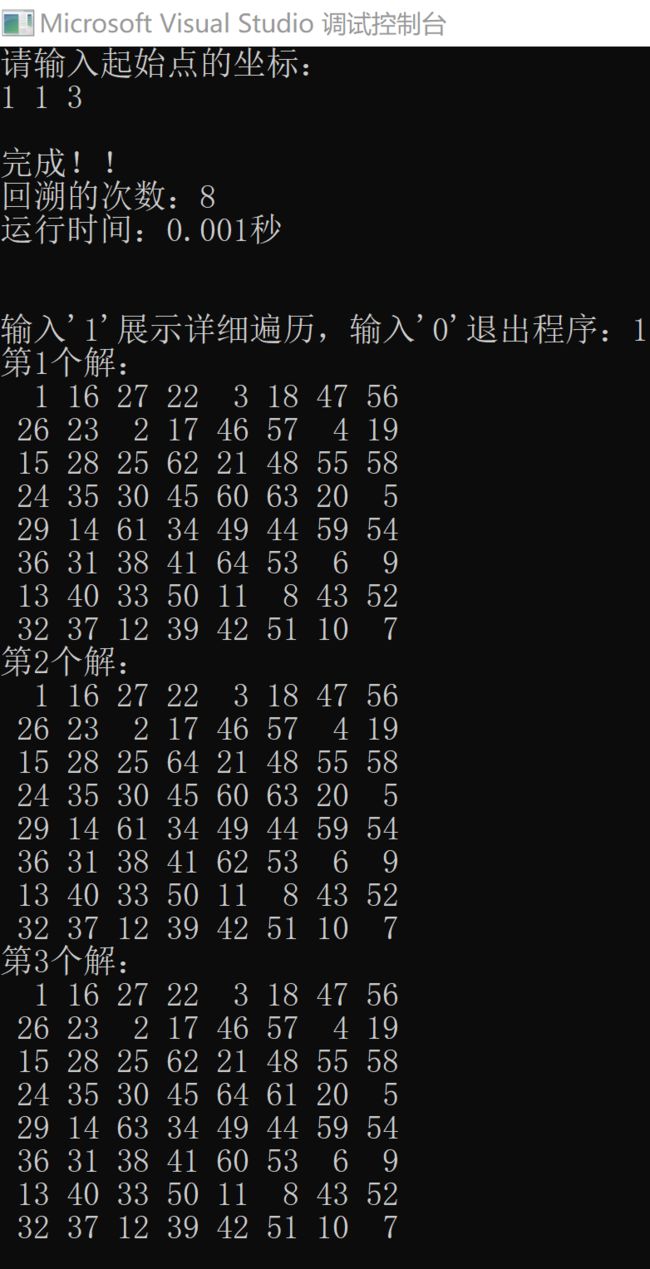
printf("请输入起始点的坐标:\n");
cin >> i >> j >> count_;
n = i * 8 + j - 9;
a[n] = 1;
return n;
}
// Sortint() 函数对点 n 的下一步进行“后续下一步可选择数”的排序,结果保存在 b[][] 里面
// c 表示前驱结点在结点 n 的哪个位置。
void Sorting(int b[64][H], int n, int c)
{
int i, j, x, y, m1, m2, k, k1, l = 1, xx, yy;
if (c != -1)
c = (c + 8 - 4) % 8;
for (i = 0; i < 8; i++) //对于当前节点的八个方向
{
F[i] = -1; //F记录八个方向的下一步的再下一步有多少个
m1 = n + f[i];
x = n / 8 + next_[i][0];
y = n % 8 + next_[i][1]; //这是下一步的坐标
if (c != i && x >= 0 && x < 8 && y >= 0 && y < 8 && a[m1] == 0) //如果下一步存在
{
F[i]++;
for (j = 0; j < 8; j++) //对于下一步的八个方向
{
m2 = m1 + f[j];
xx = x + next_[j][0];
yy = y + next_[j][1]; //这是再下一步的坐标
if (xx >= 0 && xx < 8 && yy >= 0 && yy < 8 && a[m2] == 0) //如果再下一步存在
F[i]++;
}
}
}
b[n][0] = -1;
for (i = 1; i < H; i++)
{
k = 9;
for (j = 0; j < 8; j++)
{
if (F[j] > -1 && F[j] < k)
{
k = F[j];
k1 = j;
}
}
if (k < 9)
{
b[n][l++] = k1;
F[k1] = -1;
b[n][0] = 1;
}
else
{
b[n][l++] = -1;
break;
}
}
}
// 搜索遍历路径
void Running(int n) {
int i, j, k;
int b[64][H], s[64]; // b[][] 用来存放下一步的所有后续结点排序
s[0] = n;
Sorting(b, n, -1);
while (dep >= 0)
{
if (b[n][0] != -1 && b[n][0] < H && b[n][b[n][0]] != -1)
{
k = b[n][b[n][0]];
b[n][0]++;
n += f[k];
Sorting(b, n, k);
a[n] = ++dep;
s[dep - 1] = n;
if (dep == 64)
{
for (i = 0; i < 8; i++)
for (j = 0; j < 8; j++)
print[z][i][j] = a[i * 8 + j];
z++;
if (z == count_)
{
printf("\n完成!!\n");
printf("回溯的次数:%d\n", zz);
break;
}
}
}
else
{
dep--;
zz++;
a[n] = 0;
n = s[dep - 1];
}
}
}
// 输出所有的遍历路径
void Print_()
{
int i, j, k;
printf("\n\n输入'1'展示详细遍历,输入'0'退出程序:");
scanf("%d", &count_);
if (count_)
{
for (i = 0; i < z; i++)
{
printf("第%d个解:\n", i + 1);
for (j = 0; j < 8; j++)
{
for (k = 0; k < 8; k++)
printf("%3d", print[i][j][k]);
printf("\n");
}
}
}
}
int main() {
int n;
double start, finish;
n = Prepare();
start = clock();
Running(n);
finish = clock();
printf("运行时间:%.3f秒\n", (finish - start) / CLOCKS_PER_SEC);
Print_();
return 0;
} 书写代码以后的一些感想
利用贪心以后的DFS以后代码效率明显提高了很多,但在深度搜索时print数组里的各种路径解法却是显示一样的,可能是在贪心算法中仍可能会舍弃一些解法路径导致在数组中总是存储同一种