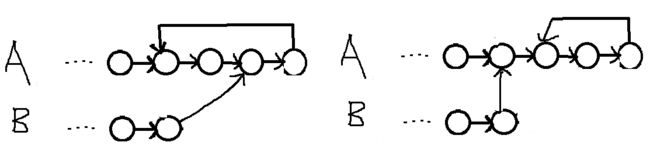问题定义
两个单向链表的头指针,两个链表都可能带环
1: 判断这两个链表是否相交
2: 如果相交,给出他们相交的第一个节点。
无环情况
判断链表是否相交
单链表相交,意味着相交结点具有相同的内存地址,且相交结点后的所有结点是两个链表共有的。
方法一:
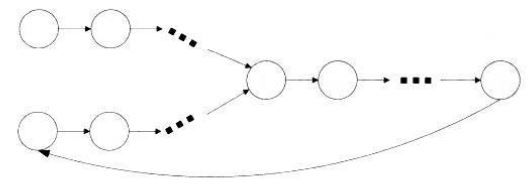
如果两条单链表相交,则将链表B,连接到链表A后面,如图所示(上面的链表是A,下面的链表是B),会形成环路,且链表B的表头一定在环上。因此我们只需要从链表B开始遍历,如果可以回到链表B的头结点,则说明两条链表相交。
时间复杂度:O(len(A)+len(B))
代码如下:
// 结点
static class ListNode{
int value;
ListNode next;
}
static boolean isIntersect1(ListNode h1, ListNode h2){
boolean isinter = false;
ListNode p1 = h1, p2 = h2;
if(p1==null || h2==null) return false;
// find the end node of list p1
while(p1.next != null) p1 = p1.next;
// append list p2 on the tail of p1
p1.next = p2;
// enumerate list p2 from its header
while(p2 != null){
if(p2 == h2) {
isinter = true;
break;
}
p2 = p2.next;
}
return isinter;
}
方法二:
单链表相交,意味着相交结点具有相同的内存地址,且相交结点后的所有结点是两个链表共有的。因此如果两个链表相交,则最后一个节点肯定是相同的,因此只需要判断两个链表的最优一个节点是否相同。
时间复杂度: O(len(A)+len(B))
代码如下:
static boolean isIntersect2(ListNode h1, ListNode h2){
ListNode p1 = h1, p2 = h2;
if(p1==null || h2==null) return false;
ListNode last1 = p1;
while(p1.next != null){
last1 = p1;
p1 = p1.next;
}
ListNode last2 = p2;
while (p2.next != null){
last1 = p2;
p2 = p2.next;
}
if(last1==last2){
return true;
}else return false;
}
寻找链表的第一个交点
先让计算链表的长度,让最长的链表A先走 len(A)-len(B)步,然后两个链表一起走,第一个相交点,即为所求的点。
static ListNode findFisrtCrossNode(ListNode h1, ListNode h2){
int lenA = len(h1);
int lenB = len(h2);
ListNode p1 = h1, p2 = h2;
ListNode tmp = null;
if(lenA > lenB) tmp = p1;
else tmp = p2;
for(int i=0; i lenB) p1=tmp;
else p2 = tmp;
while(p1!=null && p2!=null){
if(p1==p2) return p1;
p1 = p1.next;
p2 = p2.next;
}
return null;
}
static int len(ListNode h){
int clen = 0;
ListNode p = h;
while (p!=null){
p = p.next;
++clen;
}
return clen;
}
有环情况
判断链表是否有环
追逐法:
设置两个指针 fast, slow,将其初始化为链表的头结点;然后两个节点同时向前移动,fast一次移动2步,slow一次移动一步。如果存在环,fast指针和slow指针一定相遇。
static boolean hasCycle(ListNode h){
ListNode fast=h, slow=h;
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
if(fast==slow && slow!=null){
return true;
}
}
return false;
}
寻找环在链表上的入口点
当fast与slow相遇时,假设slow在环内循环了n次,fast在环内循环了m次,显然n>m,且m为0 (若有环存在,fast 必然在slow绕环一周之前与slow相遇。考虑极端情况,slow走到环入口节点时,fast位于slow前面的一个节点,记为n0,此时fast以slow指针2倍的速度绕环,当fast指针追上slow指针时, nr/2v = mr/v ==> n/2 = m == n=2m, 即当slow绕环第一周后,回到环入口节点,n=2, 已经绕环两周,并回到n0节点,由于fast指针步长等于slow的2倍,则fast指针和slow指针必然再环入口节点的前一个节点相遇)
如上图所示,当slow指针和fast直接相遇时(定义此时的节点为 相遇结点),相遇后,另p1指向头结点,p2指向相遇节点,设头结点距离环入口节点的距离: a, 头结点距离相遇节点的距离: s=a+x, 环周长:r=x+y。让p1、p2指针每次移动一步,当p1==p2时,此时就是p1(p2)指向的节点就是环入口节点。
假设在fast与slow重合时fast已绕环n周(n>0),且此时slow移动总长度为m,则fast移动总长度为2m。
2m = m+ nr = m + n(x+y) ==> m = n(x+y)
m = a+x
==> a+x = n(x+y)
==> a= n(x+y) - x = nr - x
指针p1从链表起点处开始遍历,指针p2从相遇节点处开始遍历,且p1和p2移动步长均为1。则当p1移动 a 步即到达环的入口点,由上式可知,此时p2也已移动 a 步即nr - x步。由于p2是从相遇节点处开始移动,故p2移动nr步是移回到了相遇节点处,再退 x 步则是到了环的入口点
该公式表明: 从链表头和相遇点分别设一个指针,每次各走一步,这两个指针必定相遇,且相遇的第一个点为环入口点。
代码如下:
static ListNode findCycleEntry(ListNode h){
ListNode fast=h, slow=h;
ListNode meetNode = null;
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
if(fast==slow && slow!=null){
meetNode = slow;
break;
}
}
ListNode p = h;
while(p!=null && meetNode!=null){
if(p==meetNode){
return p;
}
p = p.next;
meetNode = meetNode.next;
}
return null;
}
找出带环的两条链表相交的第一个节点
分两种情况:
1、只有一条链表带环,此时两条链表不可能相交;否则,由于相交结点后的所有结点由两条链表共享,因此导致另一条不带环的链表却出现环,导出相悖的结论。
2、两条链表都带环。如果两条链表相交,则他们共享同一个环!
带环链表相交,如图所示,存在两种情况:
1、交点在环中
2、交点不在环中
参考文献中对该问题的解决办法是首先找两个链表的相遇点,但由于相遇点值存在于环中(利用fast,slow指针的方式得到的相遇点),因此其方法不能解决交点不在环中的情况。
解决方法:
第一步:分别找出两个链表的环入口点pos1, pos2;
第二步:如果pos1==pos2, 属于第二种情况:交点不在环中。然后以pos1作为两条链表的终点,利用求不带环单链表交点的方法求出交点。
第三步:如果pos1!=pos2, 从pos1开始遍历环中的节点,如果没有发现有节点与pos2相等,则说明两条链表没有交点,否则,存在交点
第四步:分别以pos1和pos2作为终止节点,用求不带环单链表交点的方法求解。其中,必然一个有解,一个无解。取有解的那一组作为我们的答案。
参考文章:
http://blog.csdn.net/linyunzju/article/details/7753548