jdk源码分析（七）——TreeMap

一.相关概念

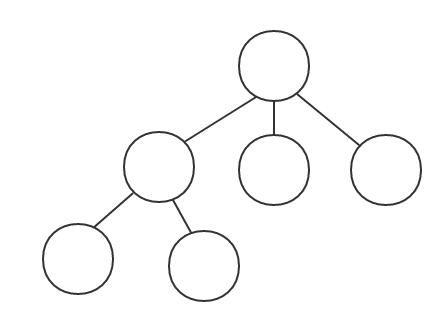
树：树是一种由n(n>=0)个节点组成的具有层次结构的数据结构。树具有一个根节点，每个节点有零个或多个子节点。

树

树的高度：树的高度指树中节点的层数。例如，上图中树的高度为3，一般将根节点的层次定为0，下一层为1，再下一层为2……。

二叉树：二叉树是一种特殊的树。每个节点最多只有两个子节点。

二叉树

二叉查找树：二叉查找树是一种特殊的二叉树。其左子树的节点中的值都小于等于根节点，右子树的节点中的值都大于等于根节点。因此，前序遍历二叉查找树，将会得到从小到大的有序列表。

二叉查找树

平衡二叉树：平衡二叉树是一种特殊的二叉查找树。它的任意节点的左右子树的高度差不超过1。平衡二叉树的高度为log(n)，其中n为节点个数。

平衡二叉树

红黑树：红黑树也是一种特殊的二叉查找树，并且平均查找性能要由于平衡二叉树。
红黑树具有如下性质：
（1）节点是红色或黑色
（2）根节点是黑色
（3）每个红色节点的两个子节点都是黑色
（4）从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

红黑树

二.类定义

TreeMap的定义如下：

public class TreeMap
    extends AbstractMap
    implements NavigableMap, Cloneable, java.io.Serializable

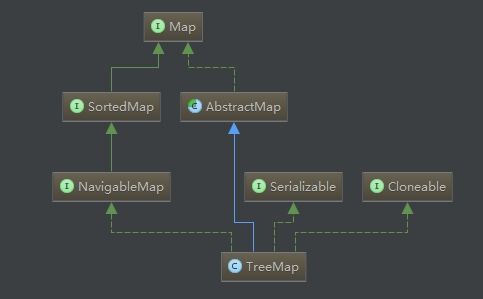
它与HashMap在类声明上的唯一区别是HashMap实现了Map接口，而TreeMap实现了NavigableMap接口。类的继承关系如下：

从图中也能够看出，NavigableMap继承自Map，它在Map的基础上增加了一些可以快速定位键值对的方法，例如lowerEntry方法可以返回小于某个给定键的最大的键值对。

三.存储结构

TreeMap基于红黑树来存储键值对：

// 比较器
private final Comparator comparator;
// 红黑树的根节点，初始时为null
private transient Entry root = null;
// 树中节点的个数
private transient int size = 0;

// 树中节点数据结构
static final class Entry implements Map.Entry {
    K key;
    V value;
    Entry left = null;
    Entry right = null;
    Entry parent;
    // 节点颜色默认为黑色
    boolean color = BLACK;

    // 构造方法
    Entry(K key, V value, Entry parent) {
        this.key = key;
        this.value = value;
        this.parent = parent;
    }
}

TreeMap的实例维护着红黑树根节点的引用，有了它，就可以方便的对树进行操作。由于红黑树是一种特殊的二叉排序树，因此在插入节点时，需要进行节点间的比较，通过comparator实例可以自定义比较器。

四.核心方法

1.构造方法

TreeMap有4个构造方法：

// 无参构造方法，使用默认的比较器
public TreeMap() {
    comparator = null;
}
// 自定义比较器
public TreeMap(Comparator comparator) {
    this.comparator = comparator;
}
// 从一个Map构造出TreeMap
public TreeMap(Map m) {
    comparator = null;
    putAll(m);
}
// 从一个SortedMap构造出TreeMap
public TreeMap(SortedMap m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

其中的核心逻辑是调用putAll方法和buildFromSorted方法。
我们先看一下putAll方法：

public void putAll(Map map) {
    int mapSize = map.size();
    // 当前树是一颗空树，并且map是SortedMap实例，而且map不是空树
    if (size==0 && mapSize!=0 && map instanceof SortedMap) {
        Comparator c = ((SortedMap)map).comparator();
        // 如果map中的比较器与当前比较器相等
        if (c == comparator || (c != null && c.equals(comparator))) {
            ++modCount;
            try {
                buildFromSorted(mapSize, map.entrySet().iterator(),
                        null, null);
            } catch (java.io.IOException cannotHappen) {
            } catch (ClassNotFoundException cannotHappen) {
            }
            return;
        }
    }
    // 否则，调用父类中的putAll方法
    super.putAll(map);
}

可见，如果当前treemap的比较器与参数map中的比较器相等的话，也会调用buildFromSorted方法，我们来看一下这个方法。

/**
 * 从sortedMap中构建红黑树
 * @param size 待构建的红黑树中节点个数
 * @param it 迭代器，如果不为空，则从迭代器中读取元素
 * @param str 对象输入流，如果不为空，则从流中读取键值对
 * @param defaultVal value默认值
 * @throws java.io.IOException
 * @throws ClassNotFoundException
 */
private void buildFromSorted(int size, Iterator it,
                             java.io.ObjectInputStream str,
                             V defaultVal)
        throws  java.io.IOException, ClassNotFoundException {
    this.size = size;
    root = buildFromSorted(0, 0, size-1, computeRedLevel(size),
            it, str, defaultVal);
}

实际构建红黑树还需要调用另一个方法，该方法是一个递归方法，会递归的构建出红黑树的左子树和右子树：

/**
 * 递归构建红黑树
 * @param level 当前树的高度，初始为0
 * @param lo 树中第一个元素的下标，初始为0
 * @param hi 树中最后一个元素的下标，初始为size-1
 * @param redLevel 红色节点的高度
 * @param it 迭代器，如果不为空，则从迭代器中读取元素
 * @param str 对象输入流，如果不为空，则从流中读取键值对
 * @param defaultVal value默认值
 * @return
 * @throws java.io.IOException
 * @throws ClassNotFoundException
 */
private final Entry buildFromSorted(int level, int lo, int hi,
                                         int redLevel,
                                         Iterator it,
                                         java.io.ObjectInputStream str,
                                         V defaultVal)
        throws  java.io.IOException, ClassNotFoundException {
  
    if (hi < lo) return null;

    // 获取正中间元素下标
    int mid = (lo + hi) / 2;

    Entry left  = null;
    if (lo < mid)
        // 递归构建左子树，由于已经有根节点了，所以level+1
        left = buildFromSorted(level+1, lo, mid - 1, redLevel,
                it, str, defaultVal);

    
    K key;
    V value;
    // 迭代器不为空，则从迭代器中读取节点
    if (it != null) {
        if (defaultVal==null) {
            Map.Entry entry = (Map.Entry)it.next();
            key = entry.getKey();
            value = entry.getValue();
        } else {
            key = (K)it.next();
            value = defaultVal;
        }
    } else { // 迭代器为空，对象流不为空，从对象流中读取
        key = (K) str.readObject();
        value = (defaultVal != null ? defaultVal : (V) str.readObject());
    }

    Entry middle =  new Entry(key, value, null);

    if (level == redLevel)
        middle.color = RED;

    if (left != null) {
        middle.left = left;
        left.parent = middle;
    }

    // 递归构建右子树
    if (mid < hi) {
        Entry right = buildFromSorted(level+1, mid+1, hi, redLevel,
                it, str, defaultVal);
        middle.right = right;
        right.parent = middle;
    }

    return middle;
}

在决定节点颜色时，调用了computeRedLevel方法：

/**
 * 给定树中节点个数，计算红色节点高度
 * @param sz 树中节点个数
 * @return
 */
private static int computeRedLevel(int sz) {
    int level = 0;
    for (int m = sz - 1; m >= 0; m = m / 2 - 1)
        level++;
    return level;
}

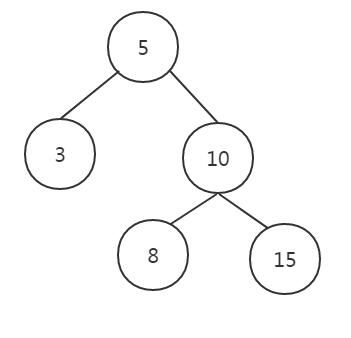
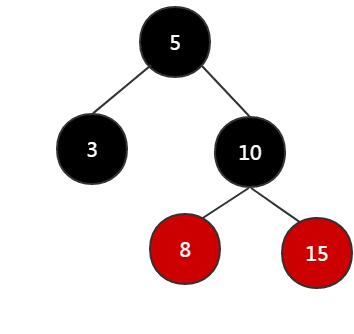
该方法的返回值实际上是树的最高层满二叉树的高度+1。例如以下树：

高度为2的层为红色

其中节点个数为5，则红色节点的高度为2。

2.put方法

public V put(K key, V value) {
    Entry t = root;
    // 当前树为一棵空树，则直接作为根节点
    if (t == null) {
        root = new Entry(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
    int cmp;
    Entry parent;
    Comparator cpr = comparator;
    // 循环，寻找插入位置，如果比根节点小，就往左子树，如果比根节点大，就往右子树
    // 循环结束时，parent为叶子节点
    if (cpr != null) { // 已有比较器
        do {
            parent = t;
            cmp = cpr.compare(key, t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else  // 插入的key与已有key相等，则覆盖
                return t.setValue(value);
        } while (t != null);
    }
    else { // 没有指定比较器也没有关系，key本身就是可比较的，实现了Comparable接口
        if (key == null)
            throw new NullPointerException();
        Comparable k = (Comparable) key;
        do {
            parent = t;
            cmp = k.compareTo(t.key);
            if (cmp < 0)
                t = t.left;
            else if (cmp > 0)
                t = t.right;
            else
                return t.setValue(value);
        } while (t != null);
    }
    Entry e = new Entry(key, value, parent);
    if (cmp < 0) // key比parent小
        parent.left = e;
    else // key比parent大
        parent.right = e;
    // 插入完成后，有可能破坏了红黑树的性质，需要进行修正
    fixAfterInsertion(e);
    size++;
    modCount++;
    return null;
}

插入的过程不是很复杂，在树中找到需要插入的位置，然后插入或者替换。插入完成后，可能会破坏红黑树的结构，因此需要进行修正：

// 节点插入后，将树调整为红黑树
// 如果调用此方法，说明发生的是节点插入，而不是替换
private void fixAfterInsertion(Entry x) {
    // 节点插入的位置为叶子节点，先置为红色，这样除了性质2不满足外，其他性质都满足
    x.color = RED;
    while (x != null && x != root && x.parent.color == RED) {
        // x的父节点在左子树上
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // y节点是x节点的叔叔节点
            Entry y = rightOf(parentOf(parentOf(x)));
            // 如果叔叔节点是红色
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else { // 叔叔节点是黑色
                // x节点是右孩子
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else { // x的父节点在右子树上
            Entry y = leftOf(parentOf(parentOf(x)));
            // 如果叔叔节点是红色
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else { // 叔叔节点是黑色
                // x是左孩子
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    // 根节点一定是黑色
    root.color = BLACK;
}

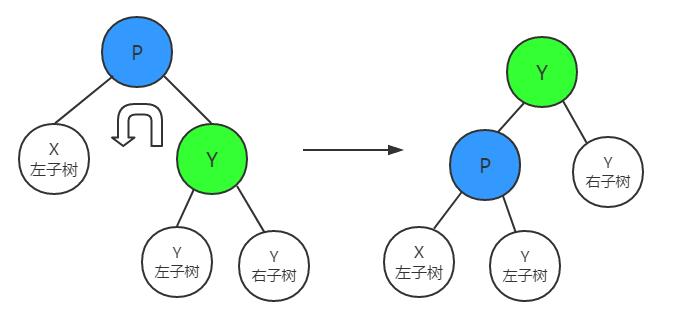
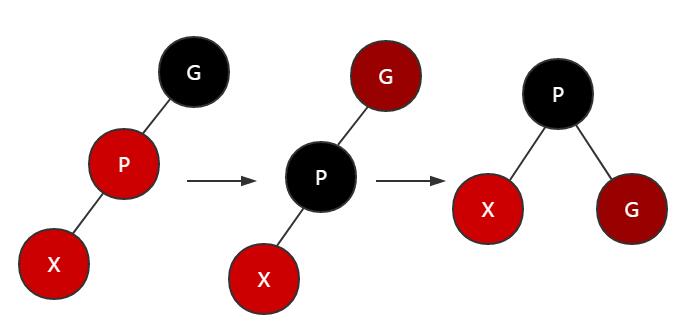
上述方法中涉及到两个子方法：rotateLeft和rotateRight，分别代表左旋和右旋，是对树的结构做的一种旋转变化。
左旋：

左旋

右旋：

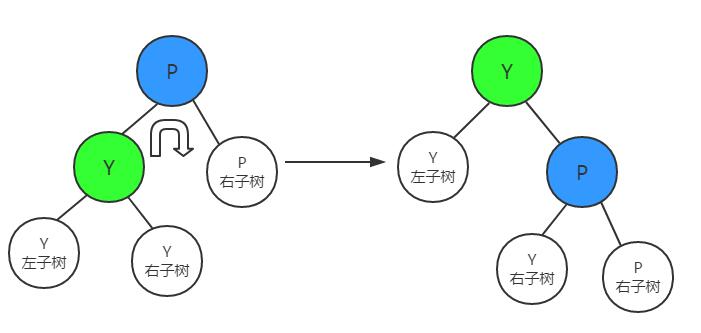
右旋

从上面代码中我们可以看到，在节点插入后，把树重新调整为红黑树的过程中主要步骤如下：
（1）判断插入节点x的叔叔节点y的颜色
（2）如果y节点是红色（此时，x节点的父节点和叔叔节点都是红色，而x节点的颜色也是红色，不符合性质三），此时将x节点的叔叔节点和x节点的父节点都改成黑色，将x节点的爷爷节点改成红色即可。
如果y节点是黑色（此时，x节点的父节点是红色，叔叔节点是黑色，而x节点是红色，不符合性质三），此时需要进行1到2次旋转，同时需要改变一些节点的颜色，有以下几种情况：
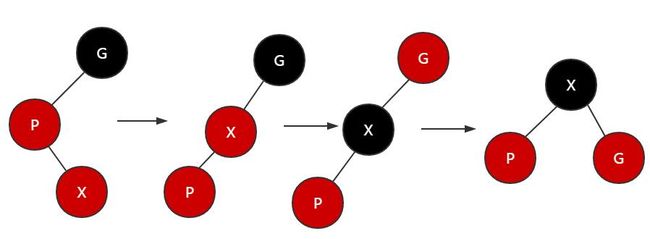
a.如果父节点在左子树，x节点在右子树，则先将父节点左旋，然后将父节点改为黑色，爷爷节点改为红色，再对爷爷节点进行一次右旋；

b.如果父节点在左子树，x节点在左子树，则只要将父节点改为黑色，爷爷节点改为红色，再对爷爷节点进行一次右旋；

c.如果父节点在右子树，x节点在左子树，则先将父节点右旋，然后将父节点改为黑色，爷爷节点改为红色，再对爷爷节点进行一次左旋（与a相反，不再画图）；
d.如果父节点在右子树，x节点在右子树，则只要将父节点改为黑色，爷爷节点改为红色，再对爷爷节点进行一次左旋（与b相反，不再画图）。

3.get方法

public V get(Object key) {
    Entry p = getEntry(key);
    return (p==null ? null : p.value);
}

final Entry getEntry(Object key) {
    if (comparator != null)
        return getEntryUsingComparator(key);
    if (key == null)
        throw new NullPointerException();
    Comparable k = (Comparable) key;
    Entry p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

get方法逻辑比较简单，由于红黑树是一棵二叉查找树，从根节点开始，将目标key值逐一与节点进行比较，直到发现节点，如果未发现，则返回null。

参考资料：

1.百度百科：红黑树
2.TreeMap中有序序列建红黑树--buildFromSorted

本文已迁移至我的博客：http://ipenge.com/10259.html