Soft Shadow Mapping综述

夜上受降城闻笛
[唐代][李益]
回乐峰前沙似雪，受降城外月如霜。
不知何处吹芦管，一夜征人尽望乡。

Shadow Mapping已经成为当前3D游戏的标配，而标准的Shadow Map算法得到的的效果过于生硬，且存在边缘的锯齿与毛刺问题，因此，一个好的软阴影实现方法变得越来越重要。

这里会将平时工作中遇到的各种软影方法简单介绍如下，起一个提炼与总结的作用。

Standard Shadow Maps

Shadow Map的基本思想：Light View画一遍Depth，然后Camera View渲场景的时候，把Pixel坐标变换到Light Space，比较Depth即可（Pixel的Depth大于Shadow Map的Depth即在阴影区）。也可以直接是Screen Space对Depth Map做Post-processing。

假设Shadow map采样的结果是d（depth），而屏幕中的像素变换到光源空间后的深度为z，那么标准的Shadow Map的计算公式可以给出如下

lighted = (d - z) > 0;

这个公式只有两个结果：0 或者 1。也就是说，使用这种方法只能得到硬阴影，要么亮要么暗，没有第三种结果。传统方法可以用Percentage Closer Filtering解决锯齿问题，也很简单，Pixel坐标对应过去之后，比较周围的多个点，计算出阴影区的百分比。此外，还可以通过Bilinear Filter让阴影更平滑，跟PCF差不多，比较相邻的4个点，然后根据Texel的Offset做插值。值得注意的是，现在的GPU都支持Hardware Shadow Map，可以直接通过tex2Dproj( u, v, z, p )这条指令实现2x2PCF+BF。

Percentage Closer Filtering（PCF）

说到软影实现，业界最出名的算法应该要算PCF了，最开始提出PCF的人，基本的想法是对周边多个像素的比对结果进行平均（模糊）处理，从而避免硬阴影的边缘毛刺问题，因此其最开始的基本实现算法是通过超采样来完成的（supersampling，也就是按照正常分辨率的多倍进行渲染，之后将阴影比对结果下采样到正常分辨率贴图从而实现软影）。

使用超采样的方式实现PCF无疑是非常耗时的，因此后面就发展出一种新的PCF方法，其实现步骤给出如下：

1.对于屏幕中的每个像素，计算出其在shadow map对应位置的模糊半径

2.对shadow map对应位置按照模糊半径采样出多个深度值

3.将采样得到的深度值与当前屏幕像素在光源空间中的深度值进行比对，每一次的比对，结果为0或者1

4.将上一步的每一次比对结果相加并除以比对次数，得到阴影数值估计

通常来说，模糊半径越大，软影效果越好，不过消耗也越高，严重情况下可以让一个FPS100的场景下降到FPS10。

PCF可以用来进行边缘软化，需要做的是：1.边缘检测；2.边缘指定大模糊半径。

Perspective Shadow Maps & Trapezoidal Shadow Maps

这两种方法沿用Shadow Map的基本思想。为了解决Shadow Map精度问题，对Depth Pass的变换矩阵做做手脚。

Exponential Shadow Maps（ESM）

ESM是Annen & Salvi提出的一种对SSM方法的改进：SSM的深度比对使用的是一个阶梯函数，得到的阴影质量边缘生硬且毛刺较多，所以尝试给出一种方法能够将阶梯比对函数替换成线性输出函数，从而能够实现输出结果的滤波，干掉毛刺，生成软影。

跟标准的Shadow Map相比，ESM有以下几点区别：

1. 采用的方法是使用指数来放大偏差：

SSM：lighted = (d - z) > 0;

ESM：lightness = saturate(exp( -c * (d - z) ) );

z为SM采样结果，而d为当前屏幕空间像素变换到光源空间后的深度值，c是一个大于0的常量。

2.存储Shadow Map的并不是原始的Depth深度值，而是经过计算的exp(c * z)指数深度值。

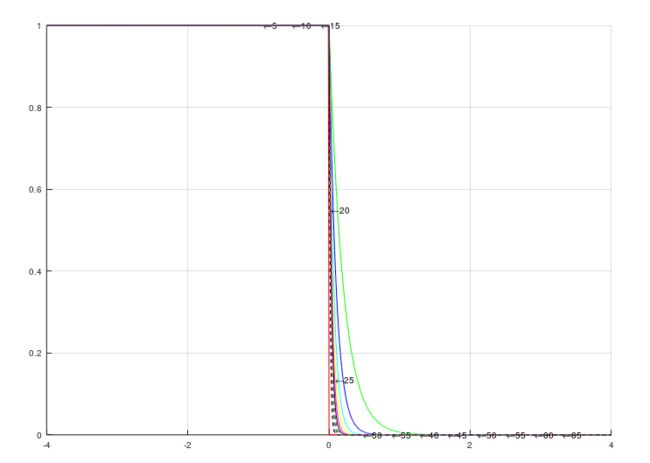
如果给定的c值足够大，那么d与z之间的细微差异都可以被明显放大，从而使用这种方式得到的结果的精度不会比SSM差，且由于其结果是一个浮点数，并不是直接的0,1值，使得这种方式计算得到的阴影是带有一定软化效果的。另外，exp(-c(d-z))=exp(-cd) * exp(cz)，因而可以将阴影的计算拆分成两个独立的项，从而分别进行滤波处理，降低误差，提升可靠性（去除毛刺）。而实际上，在渲染SM的时候，写入的是exp(cz)，之后再对SM进行一次模糊滤波，降低噪音，从而使得最终的结果更加柔软.

下图给出了不同的c值对应的曲线图，c值越小，边缘软化程度越高，误差也就越大：相对于SSM的效果而言，将部分纯阴影区域变成了半影区域，对于应该呈现软影的边缘而言，这种结果是令人满意的，而对于不应该出现软影的边缘而言，这种表现就是漏光（light-bleeding）问题，由于这种漏光通常出现在z跟d比较接近的位置，也就是投影物与承影物相接触的位置，所以通常称为接触性漏光（contact light-bleeding）。

为了避免light-bleeding，就需要使用一个尽可能大的c值，而c的取值范围如果过大，可能会超出浮点数能够表示的极限，一个解决办法就是在shadow map生成阶段，不再存储e^(c*z)，而是如SSM一样，只存储z， 之后在进行场景阴影渲染的时候再进行指数计算。 不过由于需要进行模糊处理，此时会有大量的采样计算，按照这种方式，最终的计算量会大很多，这是一种时间换空间的策略，具体是否合用需要根据实际情况进行判断。

此外，为了提高结果的可靠性，生成的ESM还可以进行一次模糊处理（模糊其实就是卷积处理），之后在使用的时候，直接用模糊后的结果乘以当前像素转换成光源空间的深度的指数形式，就得到了模糊后的saturate(exp( c * (d - z) ) );模糊的处理过程用公式来表示：

(e^( c *d ) )avg = sum(wi * e^(c * di)); for i = 0, N;

模糊处理需要对多个exp结果进行求和，由于c值比较大，可能会导致计算结果超出浮点数能够表示的最大范围，从而出现结果异常，而这个异常就会进一步限制c的可取值范围，从而增加结果的偏差。Bungie在2009的Siggraph上给出了一个叫做log-space filtering的方法，这种方法的实质是进行差异化模糊：

(e^( c *d ) )avg =

sum(wi * e^(c * di)) =

w0 * e^(c * d0) * sum(wi * e^(c * di)); for i = 1, N;

也就是说，将这些求和的分量统一除以某个数值，模糊完成之后再乘回来（实际的实现比上面的简单描述要稍微复杂一点点，会有log计算，此处简化处理了，有兴趣可以直接参考Bungie的PPT）。

使用了log-space滤波之后，可以得到更高的c值，不过也会引入新的问题，那就是mipmap跟HW滤波可能就不再可用了，因为当前数据是在log space的，而这两者使用的前提都是在linear space中。

此外，ESM的使用在receiver处于一个平面上的假设推导出来的结果，因此当这个假设不满足的时候使用ESM，可能会导致效果异常。具体可以参考Bungie2009的陈述

Variance Shadow Maps(VSM)

VSM的实现可以分成三步：

1. 在Light View计算场景的深度，与SSM不同，此处需要写入两个值：一个通道写入Depth，另一个通道写入Depth2。

2. 对这张 [Depth, Depth2] 的Texture进行Blur处理， 其目的是计算Depth与Depth2的期望值（通过对周围一定范围内的数据进行加权平均实现），这样就得到了一张 [E(Depth), E(Depth2)] 的Texture，之所以要计算这两个期望值，是为了根据方差公式 V(Depth)=E(Depth2)-E(Depth)2 计算方差。

3.根据Chebychev’s inequality（切比雪夫不等式）P(x≥t) ≤ σ2/(σ2+(t-μ)2) 式中σ2为方差V(Depth)，μ为期望E(Depth), 将Pixel坐标变换到Light Space之后的Depth代入t，得到的就是当前像素未被遮挡（shadow map depth > cur pixel light space depth）的最大概率（注意切比雪夫不等式得到的只是一个范围≤，而这里取用的是最大概率Pmax）。

不过，如上图所示，在Shadow Depth变化较大的区域（常常出现在某个像素沿着光照反方向存在多个遮挡体的情况中），VSM的方差较大，会导致漏光问题（Light bleeding）。这个问题有很多解释方式：

1.根据上面的不等式，方差较大的情况下，此时像素未被遮挡的最大概率就近似取决于方差，而(t-μ)2的影响程度较小，因而导致此时计算的结果总是接近于1，也就是说，大部分的面积都是处于光照之中的，但是实际上方差过大跟大部分面积处于光照之中其实并无必然联系，从而就会出现前面说到的漏光的问题。

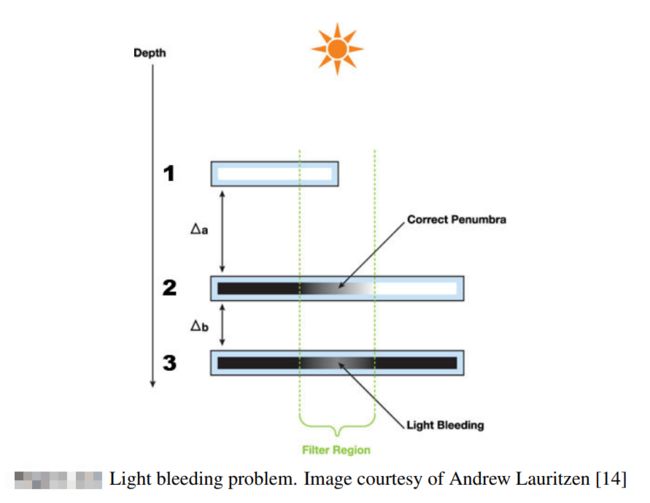
2.VSM的计算只取用了距离光源最近的物体的数据，因此对于多个物体叠加的情况下，对于上层物体（如2）以及下层物体（如3）进行阴影计算时使用的方差值就是相同的，那么对于物体2处于部分光照的区域（软影区），物体3也有可能得到同样的结果，且deltaA与deltaB的比值越大，漏光现象就越严重

为了修正这个问题，又有人提出了分层的VSM(LVSM)以及指数VSM(EVSM)方法

Summed-Area Variance Shadow Maps(SAVSM)

VSM在进行模糊处理求取各个像素的Depth以及Depth^2的深度时候，如果模糊半径过大就会导致性能下降，对于一个静态不变的模糊半径（对每个像素都相同）来说，这个数值不会太大，直接通过像素shader进行求和平均是没问题的，但是对于各个像素的模糊半径不一样，且部分像素的模糊半径非常大的时候，原来的算法就会导致一个比较高的消耗。

Lauritzen通过使用SAT来存储VSM贴图的方式解决了这个问题，这种算法可以看成是VSM的一个变种，名字就叫做SAVSM（Summed-Area VSM），SAT的意思是，每个像素中存储的不是当前像素的值，而是从原点到当前像素位置这条对角线所对应的方形区域的像素值的和（V(i, j) = V(i-1, j) + V(i, j-1) - V(i-1, j-1) + p(i,j)）。通过SAT存储的深度数据在进行模糊处理操作实现成本非常低，其成本跟模糊半径无关，是一个常量。

SAVSM的弊端在于贴图的精度会受损，如果用相同的位数来存储数据，那么最后的一个像素就需要存储整张贴图的数据之和，假设贴图像素的平均值为A，那么最后一个像素存储的结果就是WHA，这就意味着需要log2(WH)位数来存储求和导致的数据增长量，对于一个10241024的贴图，这个数值就是20bits，留给深度数据的位数就大大压缩。

数据精度的问题，目前有很多方案，比如说将深度改为使用4个通道来存储，或者用32位整数来存储，或者用双精度（在当代GPU上，此格式计算远低于整数与单精度浮点数）来存储，可惜都存在各自的问题。

Layered Variance Shadow Maps（LVSM）

为了解决VSM的Light bleeding，对光源空间按照深度范围进行分层，保证在每一层深度中，只有一个遮挡物，通过这种方式来避免VSM的漏光现象，其具体实现方式给出如下：

1.渲染shadow map，在shader中将某个像素的光源空间深度通过如下的公式，分别写入到多张shadow map中，每一张shadow map对应一层（Layer），按照下面的公式，每一层输出的深度值都是连续的，不会出现阶跃信号，其结果就相当于只有一个遮挡物：

2.在进行场景阴影渲染的时候，根据当前像素的深度选用对应层的shadow map，按照VSM的方式计算其阴影值即可（之所以不用考虑其他层，是因为比当前像素距离光源更远的层，不会对阴影有任何贡献，而更近的层，其在当前层的Shadow map中的投影值直接变成了0，已经保证了不会出现投影物贡献被忽略的情况）

可以看到，通过LVSM确实可以降低几何复杂度，有效抑制漏光问题，且由于每一层Shadow map覆盖的范围有限，因此可以使用更低精度的数据格式来实现，不过其消耗也不容忽视：1.shader中需要处理多个分支；2.需要输出数据到多张贴图中（如果不支持MRT的话，可能还会需要多个Pass才能完成）

而由于分层函数在Layer Edge处的取值分别是0与1，按照切比雪夫不等式，此时对应的概率为1与0，也就是完全点亮与完全不亮，故而按照分层VSM算法得到的阴影效果，在边缘处会出现瑕疵：

不过这个问题可以通过调整各层的覆盖范围，使之相邻两层存在一个重叠区域即可避免出现0,1的clamp：

经过这个处理后，其结果表现如下：

上面介绍了LVSM的基本思路，下面介绍一下分层算法。总的来说，如果想实现全场景质量均衡的阴影效果，那么最简单有效的就是将场景阴影深度进行均分，这样每一层的阴影质量相差不会太远；而如果想要增强某个receiver所在深度范围的阴影质量，那么就可以在这个深度范围附近多分几层。此外，从前面VSM漏光的原因来看，最好的分层方法其实是将第一个caster与第二个caster分开，或者将第二个caster跟receiver分开也行，这样receiver只对应于一个caster，从而避免漏光，那么要怎么做到完美分割场景从而实现上述目的呢？Andrew Lauritzen的文章里给出了一种基于Lloyd's Relaxation算法的递归解法，这种算法将Layer问题划分看成是一维的K-Means聚类问题来解决，有兴趣的同学可以自行翻阅。

Exponential Variance Shadow Maps（EVSM）

从名字上就可以看出来，EVSM是ESM与VSM的结合，这个方法是在waterloo大学Lauritzen在08年毕业时候的硕士论文中提出的，这种方法可以有效的解决VSM与ESM的漏光问题。

VSM中只需要计算存储[E(Depth), E(Depth2)] 两个元素，而EVSM则需要计算存储[E(exp(pos * Depth)), E((exp(pos * Depth))2), E(-exp(-neg * Depth)), E((-exp(-neg * Depth))2)]四个元素，其实就相当于对depth应用exp(posdepth)与-exp(negdepth)变换后，再进行VSM的模糊处理。

在最终计算阴影的时候，同样需要对当前像素对应的light space的深度值z进行指数处理，得到[exp(posz), -exp(-negz)]，之后则是如VSM一样，分别计算P(exp(posdepth) > exp(posz))与P(-exp(-negdepth) >-exp(-negz))的最大概率，并取其中的较小值作为输出。

其实仔细分析可以知道，在pos与neg均是大于0的情况下，如果depth>z，那么必定有exp(posdepth) > exp(posz)以及-exp(-negdepth) > -exp(-negz)，反之也是成立的，也就是说，在切比雪夫不等式的使用上面，这二者是等价的，那么为什么EVSM能够做到避免漏光问题的呢？

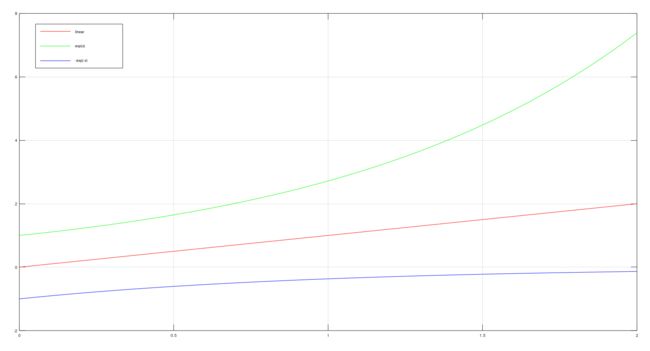
线性曲线y=x的导数为y = 1；而指数函数y = exp(x)的导数为y = exp(x);从这里可以看出，指数函数的增长率是随着x的增加而递增的，而之前说到VSM的漏光情况在deltaA与deltaB的比值越大的情况下越严重，deltaA与deltaB可以看成是距离光源距离x的差分函数，当使用了指数函数之后，此时的deltaA由于距离光源更近，所以其数值的增长速度会低于deltaB的增长速度，从而导致deltaA/deltaB的比值得以降低，且1跟2的位置差距越大，c值越大，此降低的比例也就越大，从而达到避免漏光的效果。

如果只是出于修正VSM漏光的考虑，那么只需要一个pos的系数的指数函数就已经足够，为什么还需要一个neg系数的指数函数呢？实际上只使用pos系数的指数函数的话已经能够消除VSM的漏光问题，不过ESM在非平面receiver的情况下，也会存在漏光问题，因此需要引入neg系数的指数函数。那么neg系数的指数函数是如何做到避免ESM的漏光现象的呢？

从上面的图中可以看出，exp(x)的斜率是递增的，而-exp(-x)的斜率是递减的。如果正系数的指数函数的作用效果是降低deltaA/deltaB的数值的话，那么负系数的指数函数的作用效果就是降低receiver与caster之间的depth差值。那么这个效果有什么意义呢？从前面知道ESM方法的假设是d > z;（z是采样结果，d是当前像素深度），为什么要有这个假设呢，从文章中知道，ESM之的sum(wi * exp(c * (zi - d))是从sum(wi * 1/(1+exp(c*(d - zi))))由假设d > zi且c无穷大简化而来，而如果采样半径比较大的话，就有可能采样到某个像素的深度zi小于d，那么此时这个推导就不成立了，而将错误的推导直接用于计算阴影，就会导致漏光，这就是为什么需要保证receiver为planar的原因了（可以保证d与zi之间的差异不至于过大）。

对于ESM的漏光问题，d与zi之间的差值越大，漏光现象越明显，采样半径越大，问题越严重。而通过使用一个neg系数的指数，可以降低d与zi之间的差值，从而减轻漏光（好像不是很合理，毕竟EVSM使用的不是ESM的计算公式，而是VSM的计算公式）

从效果上来看，EVSM的效果是非常好的，其缺陷在于需要一张额外的四通道贴图用于存储新增的四个数据项，且如果c值过大，依然可能会导致溢出问题。

Convolution Shadow Maps

CSM提出了一种非常好的图形学算法思路。其推导过程比较华丽，用到了几个数学上的概念：卷积，傅里叶级数。（注意还有另外一种CSM – Cascaded Shadow Maps，两者作用是不一样的）

首先，假设x⊆R3为某一点的世界坐标，d(x)为该点到Light Source的距离（也就是Light Space的Depth）。p⊆R2为该点对应到Shadow Map上的坐标，z(p)为该点对应的Shadow Map上的Depth。于是可以定义一个Shadow Test函数：

s(x) = f(d(x), z(p)) 当d>z时，s为0，反之为1

为了得到软阴影，我们希望能对s进行卷积，即希望得到：

sf(x) = ∑w(q)f(d(x),z(p-q)) = w*f(d(x), z)（亮点1）

如果能对上式运用卷积定理，得到如下式的结果，则表明可以通过对z(p)做卷积而得到软阴影。（即可以利用Blur、硬件Bilinear Filter和Mipmap来达到软阴影）

w*f(d(x), z) = f(d(x), w*z)

可惜的是，f(d(x), z(p))并不是线性函数（而是阶跃函数），无法对其运用卷积定理。为此，CSM转而采用数值分析方法，用傅立叶级数来逼近函数f。（亮点2）

虽然CSM的推导过程相当华丽，但是本身缺点太多（比如：内存开销较大，Shadow Map Pass需要输出的数据量太大，带宽内存都吃得太紧），导致其实用价值很低。