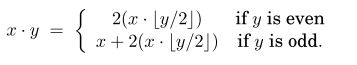1.1Basic arithmetic
1.1.1addition
-Given two binary numbers x and y, how long does our algorithm take to add them?
-We want the answer expressed as a function of the size of the input: the number of bits of x and y, the number of keystrokes needed to type them in.
Suppose x and y are each n bits long; O(n).
1.1.2multiplication
二进制乘法的两个算法:
If x and y are both n bits, then there are n intermediate rows, with lengths of up to 2n bits (taking the shifting into account). The total time taken to add up these rows, doing two numbers at a time, is O(n) + O(n) + · · · + O(n)..(n-1 times): O(n^2)
function multiply(x, y)
Input: Two n-bit integers x and y, where y ≥ 0
Output: Their product
/
if y=0: return0
z = multiply(x, ⌊y/2⌋)
//每次递归调用,接收到返回值之后 向递归下一步执行
if y is even:
return 2z
else:
return x + 2z
function divide(x,y)
Input: Two n-bit integers x and y, where y ≥ 1
Output: The quotient and remainder of x divided by y
/
if x = 0: return (q,r) = (0,0)
(q, r) = divide(⌊x/2⌋, y)
q=2·q, r=2·r
if x is odd: r=r+1
if r≥y: r=r−y, q=q+1
return (q,r)
1.2mod
if x = qN + r with 0 ≤ r < N, then x modulo N is equal to r.
x and y are congruent modulo N if they differ by a multiple of N , or in symbols:
x≡y (modN) ⇐⇒ N divides (x−y).
Substitution rule
If x ≡ x′ (mod N) and y ≡ y′ (mod N), then:x+y≡x′+y′ (modN) and xy≡x′y′ (modN).Modular addition and multiplication:
addition: O(n),
n = ⌈log N ⌉ is the size of N ;(regard N as a binary number, n is the bits of this number, each bits need one operations)
To add two numbers x and y modulo N, Since x and y are eachin the range 0 to N −1, their sum is between 0 and 2(N −1), The overall computation therefore consists of an addition, and possibly a subtractionmultiplication: O(n^2)
using our quadratic-time division algorithm.Multiplication thus remains a quadratic operation.Division: O(n^3)
- Modular exponentiation
-Problem: compute x^y mod N for values of x, y, and N that are several hundred bits long
-Sol1: x mod N →x^2 mod N →x^3 mod N →···→x^y mod N,
-Sol2: x mod N →x^2 mod N →x^4 mod N →x8^ mod N →···→x2^⌊logy⌋ mod N.
a polynomial time algorithm:
function modexp(x, y, N)
Input: Two n-bit integers x and N, an integer exponent y
Output: x^y mod N
/
if y=0: return1
z = modexp(x, ⌊y/2⌋, N )
if y is even:
return z^2 mod N
else:
return x · z^2 mod N
- Euclid's Alg for Great Common Divisor
Euclid’s rule If x and y are positive integers with x ≥ y, then gcd(x, y) = gcd(x mod y, y).
Lemma If a ≥ b,then a mod b < a/2.
function Euclid(a,b)
Input: Two integers a and b with a≥b≥0
Output: gcd(a, b)
/
if b=0: return a
return Euclid(b, a mod b)
both arguments, a and b, If they are initially n-bit integers, then the base case will be reached within 2n recursive calls. And since each call involves a quadratic-time division, the total time is O(n3).
Lemma if d divides both a and b, and d = ax + by for some integers x and y(may be negative) , then necessarily d = gcd(a,b)
function extended-euclid(a,b)
Input: Two positive integers a and b with a ≥ b ≥ 0
Output: Integers x,y, d, such that d=gcd(a,b) and ax+by=d
/
if b = 0: return (1,0,a)
(x′, y′, d) = Extended-Euclid(b, a mod b)
return (y′, x′ − ⌊a/b⌋y′, d)
模除法:gcd(a,N) = 1(即互质) <==> 存在x,使得ax ≡ 1 (mod N) (可用反证法证明)
左推右:用extend-euclid algorithm可以得到x,y
右推左:如果ax+Ny=d(gcd<=d), 且d整除a, N(d <=gcd),那么d==gcd(a, N)
- x is the multiplicative inverse of a modulo N if ax ≡ 1 (mod N).
Modular division theorem For any a mod N, a has a multiplicative inverse modulo N if and only if it is relatively prime to N. When this inverse exists, it can be found in time O(n3)(where as usual n denotes the number of bits of N ) by running the extended Euclid algorithm.
1.3prime
function primality(N)
Input: Positive integer N
Output: yes/no
/
Pick a positive integer a < N at random
if a^(N−1) ≡ 1 (mod N):
return yes
else:
return no
exercise都是clrs上的不附了