排序_堆与堆排序

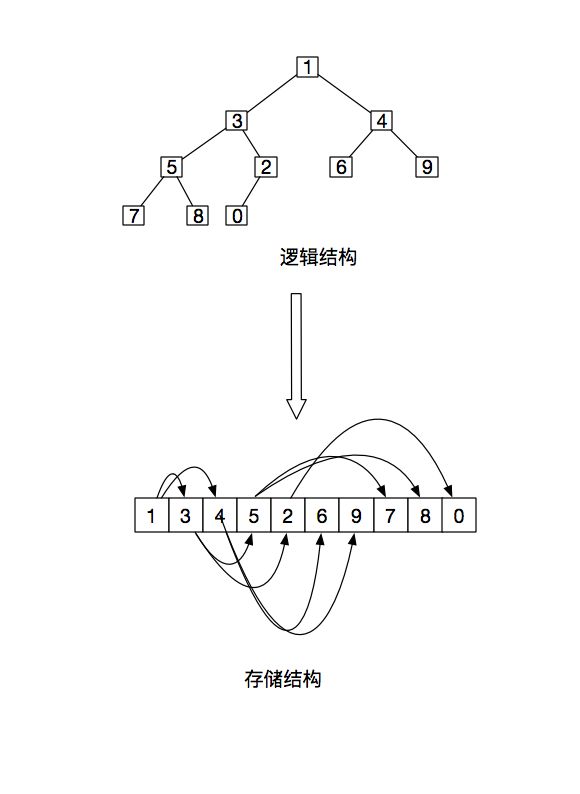
与简单选择排序的关系

简单选择排序过程有这个问题：在待排序的n个记录中选择一个最小的记录需要比较n-1次。这样的操作并没有把每一趟的比较结果保存下来，这样导致的问题是在后一趟的比较中，有许多比较在前一趟就已经做过了。如果可以做到每次在选择的最小记录的同时，并根据比较结果对其它记录做出相应的调整，这样排序的总体效率就会提高。堆排序就是对简单选择排序进行的一种改进。

二叉堆（binary heap）

堆(堆结构)是一种特殊的树形数据结构。
一般来说堆指的是二叉堆。因为其它几种堆用的很少，例如：二项式堆，斐波纳契堆等。

二叉堆具有下列性质的顺序存储的完全二叉树：
1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。
2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

二叉堆有两种：最大堆和最小堆。
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；
最小堆：父结点的键值总是小于或等于任何一个子节点的键值。

完成二叉树的简单介绍请看：数据结构之树的介绍

二叉堆的存储结构

二叉堆一般用数组来表示。结点i的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2i + 1和2i + 2。例如，根节点在数组中的位置是0，第n个位置的子节点分别在2i+1和 2i+2。因此，第0个位置的子节点在1和2，1的子节点在3和4，以此类推。这种存储方式便於寻找父节点和子节点。

我们可以知道总结以下：
二叉树的结点下标位置与该结点存储在数组的下标索引一一对应。

二叉堆的逻辑结构和存储结构图

建立堆以及二叉堆的三种操作

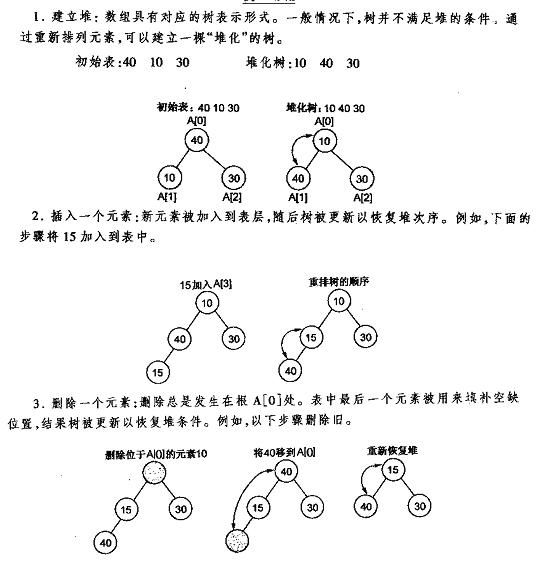
下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解。

建立堆和插入删除图例

初始化堆操作

// 堆排序的第一个过程：建立堆
    private void 初始化堆(int[] array) {
        /**
         * 问题： 1. 为什么i初始值为array.length / 2？ 答：刚好这个值在树的叶子结点上
         */
        for (int i = array.length / 2; i >= 0; i--) {
            对某个结点建立最大堆(array, i, array.length - 1);
        }

    }

    /**
     * 给定一个任意结点，以这结点为根节点的树，进行建立堆操作。 使得当前结点的左右子树都是二叉堆。
     * 
     * @param array
     *            待排序的序列
     * @param parent
     *            节点在序列中的位置
     * @param length
     *            数组长度，此长度的值可能是虚构
     */
    private void 对某个结点建立最大堆(int[] array, int parent, int length) {

        int temp = array[parent];
        int child = 2 * parent + 1;

        while (child < length) {

            // 取左右孩子的值大的那个
            if (child + 1 < length && array[child] < array[child + 1]) {// 有右孩子，并且右孩子比左孩子大
                child++;// 自增1，此时表示右孩子的索引
            }

            // 父节点大于子节点，满足条件方法终止执行
            if (temp > array[child]) {
                break;
            }

            /**
             * 父节点与子节点交换，使得父节点比子节点大
             */

            // 把孩子结点的值赋给父结点
            array[parent] = array[child];

            // 把孩子结点作为新的父节点
            parent = child;
            // 选取孩子结点的左结点，继续向下筛选
            child = 2 * child + 1;

        }

        // 如果parent的左孩子结点不存在，有以下操作
        array[parent] = temp;

    }

对于二叉堆我们通常有三种操作：插入、删除和修改元素。

堆的插入

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的序列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。

堆的删除

为了便于重建堆，每次都只删除根节点，表中最后一个元素赋值给根节点并且用来补空缺位置，最后重新恢复堆。相当于从根结点将一个数据的“下沉”过程。

    /**
     * 堆排序的第二个过程：堆顶与堆的最后一个元素交换位置，每交换完后重新恢复堆
     * 
     * @param array
     */
    
    private void 堆排序(int[] array) {

        // 每次循环遍历后执行i--，使最后一位不比较了，达到删除效果
        for (int i = array.length - 1; i >= 0; i--) {

            // 堆的最后一位和第一位交换位置
            int temp = array[i];
            array[i] = array[0];
            array[0]= temp;

            // 重新恢复堆操作
            对某个结点建立最大堆(array, 0, i);
            System.out.format("第 %d 趟: \t", array.length - i);
            printPart(array, 0, array.length - 1);
        }
    }

堆的修改

待补充

堆排序

基本思想：开始时把待排序的序列看作是一棵顺序存储的二叉树，接着对此序列进行堆化操作使其成为一个最大堆(或最小堆)

堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置

处理流程：

• 第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。
• 第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。
• 由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。

堆排序完整代码：

/**
 * @author yeoggc
 */
public class 堆排序code_1 {

    public static void main(String[] args) {
        int[] sequence = new int[]{50, 10, 90, 30, 70, 40, 80, 60, 20};//待排序的关键字序列
        System.out.println("排序前：" + Arrays.toString(sequence));
        heapSort(sequence);
        System.out.println("排序后：" + Arrays.toString(sequence));
    }

    private static void heapSort(int[] sequence) {
        /**
         * 堆排序的第一个过程：建立堆。即，把无序序列构建成一个大顶堆
         * i取值范围是[sequence.length / 2 - 1 , 0],
         * 表示的是从下往上，从右到左，将每个非叶子结点当作根节点，
         * 将其和其子树调整成堆。
         */
        int i;
        for (i = sequence.length / 2 - 1; i >= 0; i--) {
            heapAdjust(sequence, i, sequence.length);
        }

        /**
         * 堆排序的第二个过程：堆顶记录和当前未经排序子序列的最后一个记录交换，每交换完后重新恢复堆
         */
        for (i = sequence.length - 1; i > 1; i--) {
            swap(sequence, 0, i);
            heapAdjust(sequence, 0, i - 1);//重新调整为最大堆
        }

    }

    @SuppressWarnings("Duplicates")
    private static void heapAdjust(int[] sequence, int s, int m) {

        int temp, j;
        temp = sequence[s];

        for (j = s * 2 + 1; j < m; j = 2 * j + 1) {//通过for循环找到每个结点的左孩子
            // j < m - 1用于判断是否有右孩子结点；sequence[j] < sequence[j + 1]用于判断右孩子结点是否大于左孩子结点
            //如果满足两个条件j就自增，指向较大的孩子结点
            if (j < m - 1 && sequence[j] < sequence[j + 1]) {//沿关键字较大的孩子结点向下筛选
                j++;
            }

            //当前子树的根节点的值大于它的孩子结点的值，符合最大堆要求，直接结束循环
            if (temp > sequence[j]) {
                break;
            }

            //把较大值结点的值赋值给父节点
            sequence[s] = sequence[j];
            //以j为根节点的子树在进行最大堆操作
            s = j;
        }
        sequence[s] = temp;
    }

    private static void swap(int[] sequence, int i, int j) {
        int temp = sequence[i];
        sequence[i] = sequence[j];
        sequence[j] = temp;
    }
}

算法分析

• 堆排序的运行时间主要是消耗在初始构建堆和在重建堆时的反复筛选上。
• 由于初始构建堆所需的比较次数较多，因此，它并不适合待排序序列个数较少的情况。

算法时间复杂度和空间复杂度

时间复杂度：
由于堆排序对原始记录的排序状态并不敏感，因此无论是平均情况，最好情况，最坏情况都是O(nlogn)。这在性能上远远好过于冒泡、简单选择、直接插入的O(n^2)的时间复杂度。

空间复杂度：它只有一个用来交换的暂存单元，所以控件复杂度为O(1)。

备注：
O()代表不超过括号内数值的最大整数值。
n*log2(n) n乘以2为底的n对数

算法稳定性

堆排序是一种不稳定的排序方法。

• 因为在堆的调整过程中，关键字进行比较和交换所走的是该结点到叶子结点的一条路径，因此对于两个相同关键字原来的先后顺序会改变。
• 由于记录的比较与交换是跳跃式进行的。