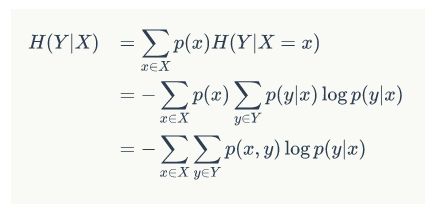决策树常见划分原则信息熵、条件熵、信息增益、信息增益比、基尼指数的一般化描述

信息熵

信息熵就是度量信息的不确定度，例如现在总共10份数据，其中5份正5份负，那么正负的概率就是0.5

image.png

根据这个公式，来计算信息熵，p(xi)代表每一类的概率，这样计算出来的值代表目前数据的不确定度。

条件熵

我们知道条件概率，p（y|x）就是在X的条件下我们计算Y的概率
那么条件熵也是相同的，就是我们先按照X做为分类标准，再计算以Y作为分类标准的熵值。

image.png

这里的H（y|x）就是我们如果按照X先进行分类之后，再以Y分类的信息熵
条件熵是另一个变量Y熵对X（条件）的期望
其实条件熵意思是按一个新的变量的每个值对原变量进行分类，比如上面这个题把嫁与不嫁按帅，不帅分成了俩类。

然后在每一个小类里面，都计算一个小熵，然后每一个小熵乘以各个类别的概率，然后求和。

我们用另一个变量对原变量分类后，原变量的不确定性就会减小了，因为新增了Y的信息，可以感受一下。不确定程度减少了多少就是信息的增益。

信息增益

信息增益恰好是：信息熵-条件熵。
（解释：如果目前Y代表lable，那么H（Y）就是当前的信息熵，H（Y|X）代表以X特征作为分类条件的lable信息熵，两者相减就是如果使用X特征进行分类所获得的信息增益，如果信息增益为正的话那么按照X分类后的不确定度降低）

换句话说，信息增益代表了在一个条件下，信息复杂度（不确定性）减少的程度。那么我们现在也很好理解了，在决策树算法中，我们的关键就是每次选择一个特征，特征有多个，那么到底按照什么标准来选择哪一个特征。这个问题就可以用信息增益来度量。如果选择一个特征后，信息增益最大（信息不确定性减少的程度最大），那么我们就选取这个特征。

信息增益比

以信息作为划分训练数据的特征，存在偏向选择取值较多的特征的问题，使用信息增益比可以校正这一问题。
信息增益比等于特征A的信息增益g(D,A)除以,训练数据集D关于在特征A下的熵H（D）的比值。

image.png

image.png

基尼系数

基尼指数（ CART算法 ---分类树）
定义：基尼指数（基尼不纯度）：表示在样本集合中一个随机选中的样本被分错的概率。

注意： Gini指数越小表示集合中被选中的样本被分错的概率越小，也就是说集合的纯度越高，反之，集合越不纯。
即 基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

书中公式：

image.png

说明:

1. p_k表示选中的样本属于k类别的概率，则这个样本被分错的概率是(1-p_k)

2. 样本集合中有K个类别，一个随机选中的样本可以属于这k个类别中的任意一个，因而对类别就加和

3. 当为二分类是，Gini(P) = 2p(1-p)

**样本集合D的Gini指数 ： **假设集合中有K个类别，则：

image

基于特征A划分样本集合D之后的基尼指数：

需要说明的是CART是个二叉树，也就是当使用某个特征划分样本集合只有两个集合：1. 等于给定的特征值 的样本集合D₁ ， 2 不等于给定的特征值 的样本集合D₂

实际上是对拥有多个取值的特征的二值处理。

举个例子：
假设现在有特征 “学历”，此特征有三个特征取值： “本科”，“硕士”， “博士”，

当使用“学历”这个特征对样本集合D进行划分时，划分值分别有三个，因而有三种划分的可能集合，划分后的子集如下：

1. 1. 划分点： “本科”，划分后的子集合 ： {本科}，{硕士，博士}

   2. 划分点： “硕士”，划分后的子集合 ： {硕士}，{本科，博士}

   3. 划分点： “硕士”，划分后的子集合 ： {博士}，{本科，硕士}

      对于上述的每一种划分，都可以计算出基于 划分特征= 某个特征值 将样本集合D划分为两个子集的纯度：

image.png

因而对于一个具有多个取值（超过2个）的特征，需要计算以每一个取值作为划分点，对样本D划分之后子集的纯度Gini(D,A_i)，(其中A_i 表示特征A的可能取值)**
然后从所有的可能划分的Gini(D,A_i)中找出Gini指数最小的划分，这个划分的划分点，便是使用特征A对样本集合D进行划分的最佳划分点。