一、
复活节这几天在家休假,昨天看到国内虐娃群的一道初中物理题。
群里有直接说不会做的朋友,他们的孩子大多还小,还在忙于跟进小学三四年级的奥数题、或者忙于准备小升初的材料。有选C的朋友,他们要么孩子正在读初中,要么还能从自己遥远的记忆中依稀找到初中物理速度分量的概念。
不过,正确答案是B。
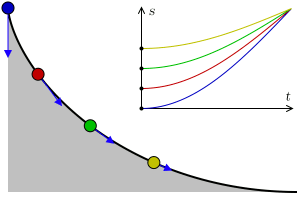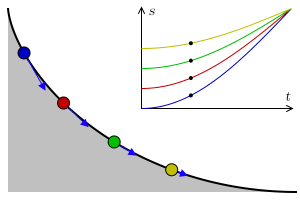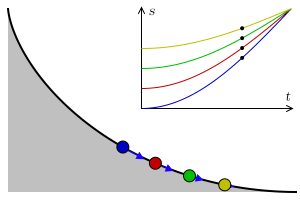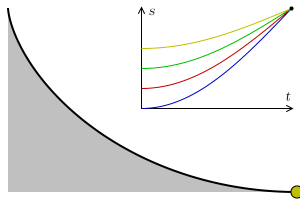
b球从M到轨道最低处的过程,根据机械能守恒,是势能向动能转化的过程。由于在轨道谷底处b球并不存在垂直的速度分量,所以在此处b球水平方向的速度必然大于a、b两球的水平初速度v0。与之类似,b球从轨道最低处到N的过程,是动能向势能转化的过程,b球的水平速度逐渐减小至v0。由于a球在整个过程保持匀速v0,而b球的水平速度始终大于或者等于v0,可知答案为B。
由此展开,
- 如果轨道不是下凹形而是上凸形,那么b球将始终慢于a球,且存在初始动能不足以越过轨道高点势能阱的可能。
- 由机械能守恒可知,轨道最低处和M点的高度差决定了b球在最低处的速度,也就是整个过程中b球最大的水平速度。
如果高度差一定,根据机械能守恒,最低处的速度也将相同,那么是不是不论通过何种形态的轨道曲线b球从M到最低点所需的时间也恒定呢?
二、
1697年的复活节,瑞士巴塞尔。
数学家约翰・伯努利(Johann Bernoulli)的书桌上躺着五份关于上述问题的解答,即“垂直平面中小球沿何种曲线下降将最先到达底部”。这个问题又被称之为“最速降线问题”,大名鼎鼎的伽利略于1630年提出了这个问题,当时伽利略认为最速降线的答案是圆弧。
这个悬而未决的问题在几十年后被再次提起,约翰・伯努利在期刊Acta Eruditorum上宣称他已经得到了答案,并向全欧洲的数学家征集其它可能的解答,约定的比赛截止日期为1697年的复活节。
现在,约翰・伯努利手头上有了四份答复,分别来自于他同为数学家的哥哥雅各布・伯努利(Jakob Bernoulli),跟随他学习微积分的学生纪尧姆·德·洛必达(Guillaume François Antoine, Marquis de l'Hôpital),他的微积分老师莱布尼茨,以及一封来自英国的匿名解答。
“不用看都知道,这匿名解答来自于牛顿。”约翰・伯努利十分肯定。因为牛顿和莱布尼茨在微积分理论上的一些分歧,以及莱布尼茨和约翰・伯努利之间的师生关系,很显然牛顿不愿意以正常方式参加这次伯努利主持的公开挑战。
好在科学并不以科学家之间的个人恩怨为转移,四份解答,加上约翰・伯努利自己的解答,全都指向了最速降线的正确答案——摆线。
三、
摆线(cycloid),即圆周上某一个点在该圆沿直线运动时形成的轨迹。
说来很有意思,伽利略是深入研究过摆线的科学家之一,甚至为摆线命名的也恰恰就是伽利略,然而他在最速降线这个问题上却错过了摆线这个正确答案。
此外,摆线还有个外号,叫做“几何学中的海伦”。海伦是希腊神话中的绝世美女,引来了众多追求者之间的争斗,特洛伊战争也是因她而起。
说摆线是几何学中的海伦,一方面是因为这条曲线本身确实很优美,从数学的角度来说,她有着很多美丽的特性,比如摆线的长度是生成它的圆的直径的四倍,又比如摆线下方的面积是生成它的圆的面积的三倍。和最速降线相关的特性是,如果在摆线上任意多点上摆放多个小球,同时松开小球,所有的小球将同时到达底部。
另一方面因为摆线的优美,不少著名数学家都热心于摆线的研究,这里包括笛卡尔、帕斯卡、梅森、惠更斯、约翰・伯努利、莱布尼兹和牛顿等,每一个人都是科学史上大师级的人物。而正是因为摆线美丽的数学特性和众多大师级的追随者,从1599年伽利略命名摆线开始,直到1697年伯努利的复活节之约,这一百年内围绕着摆线的纷争从未平息。
继伽利略和梅森之后,罗伯瓦尔(Gilles de Roberval)于1628年也开始研究摆线。1634年,罗伯瓦尔证明了摆线下方的面积是生成它的圆的面积的三倍,他采用的方法帮助他赢得了皇家学院数学领域的席位,由于该席位每三年需要重新竞选,所以罗伯瓦尔决定不公开发表已经取得的关于摆线的其它一些研究成果,以便在下一次竞选中使用它们。罗伯瓦尔因此成功地在皇家学院待了40年,期间有不少其他数学家陆续发表了关于摆线的一些成果,罗伯瓦尔都声称他对此早有定论,因为并无公开发表的论文支持他,这些争论一直不能平息。其中最有名的争论是关于摆线面积和切线关系的解释,曾经担任过伽利略助手的托利切里于1644年发表了相应的结果却遭到了罗伯瓦尔的指控,后者认为前者剽窃了他的成果。现在的历史学家一般认为,托利切里的成果确实来自于他自己的独立研究。
1658年,帕斯卡在摆线研究上取得了一些新的进展,他决定针对这些问题设立一个公开挑战赛,并为收集到的最佳解答设立一等奖和二等奖。为了保证公正性,帕斯卡邀请了罗伯瓦尔担任评委之一。不过出乎帕斯卡意料的是,挑战赛仅仅收到两套解答,经过讨论,帕斯卡和罗伯瓦尔认为这两套解答水平不足以获奖,拒绝为两位参赛者提供奖金。相反,帕斯卡将自己的研究进展发表,并写了一篇名为《摆线历史》的文章,文章中在谈到罗伯瓦尔和托利切里的争论时,帕斯卡明显地选择站在罗伯瓦尔一边。
1697年复活节之约的五份解答都得到了关于最速降线的正确答案,但伯努利兄弟俩都坚持自己是第一个得出答案的人。兄弟俩互相指责对方剽窃了自己的成果,为此两人争吵了很多年,后世认为虽然约翰的解答比较巧妙,但雅可布的解答要更为完备和准确。再后来,约翰・伯努利和他的天才儿子丹尼尔·伯努利在流体力学方面的成果也展开了争夺,后者最终保卫了自己“伯努利定律发明者”的荣誉。
祖上从比利时安特卫普迁往瑞士的伯努利家族在十七世纪十八世纪一共培养出了八位著名的科学家或数学家,然而荣誉之争、口舌之战却发生在亲兄弟和亲父子之间,也是可悲!
四、
与希腊神话中的海伦不同,“几何学中的海伦”在现实生活中随处可见。
在中国古典的建筑中,歇山顶的坡面即是摆线设计,这一设计使得暴雨中雨水能够以最快的速度排走,从而减小过大的雨水量对屋顶带来的负荷。
在游乐园里,过山车的轨道也采用摆线设计,使得游客们能够最快地到达轨道底部,以及,面对最大的惊悚。水上乐园的滑道、高台滑雪的滑道以及滑板比赛的U型台都采用类似的设计,不过考虑到无法避免的阻力以及其它非理想因素,实际中的轨道或者滑道曲线和摆线略微有些不同。
参考出处:
1.http://imgsrc.baidu.com/forum/w%3D580/sign=5a9eb26baf6eddc426e7b4f309dab6a2/b3e2d0160924ab18c3417db937fae6cd7a890b69.jpg
2.https://zh.wikipedia.org/wiki/%E6%91%86%E7%BA%BF#/media/File:Cycloid_f.gif
3.http://www.guokr.com/post/626156/
4.http://baoding.cncn.com/article/103516/
5.http://news.xinhuanet.com/tech/2013-06/05/c_124703653.htm
6.http://v.qq.com/x/search/?q=%E6%BB%91%E6%9D%BF%E6%AF%94%E8%B5%9B&stag=txt.playpage.vppdesc
文/Athlon_BE
2017.4.12 初稿
2018.4.5 二稿