前言:过一些基础知识,来吧。
乘法
通常,高级语言中两个 n 位整数相乘得到的结果通常也是一个 n 位整数,也即结果只取 2n 位乘积中的低 n 位
int mul(int x, int y) {
int z = x*y;
return z;
}
x*y 被转换为乘法指令,在乘法运算电路中得到的乘积是 64 位,但是,只取其低 32 位赋给 z。
在计算机内部:一定有 吗?
- x 是带符号整数,则不一定
- x 是浮点数,则一定
只有 4 位存储时,
那么在程序里面如何判断溢出呢?
!x || z/x == y;
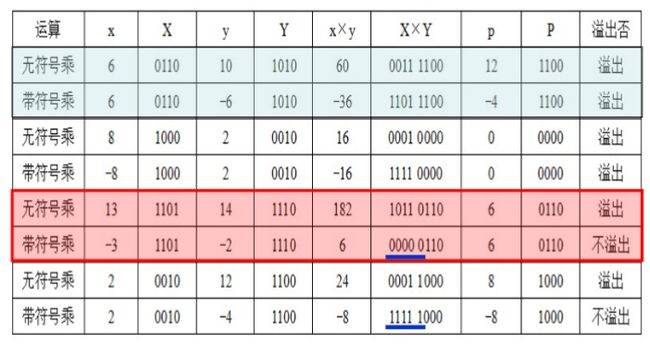
现在我们来看看,无符号乘法和有符号乘法之间的规律(假设只有 4 位存储)
根据运算的规律,在相同的机器数下,无符号乘法与有符号乘法的低 n 位运算结果相同,也就是说,有符号和无符号乘法可以用同一个运算器计算。只保留低 n 位。
同样可以根据上述的规律可以总结出:
- 无符号:若高 n 位全为 0,则不溢出,否则溢出
- 带符号:若高 n 位全为 0 或全 1,且等于低 n 位的最高位,则不溢出
为了判断溢出我们得知道:
- 硬件不判断溢出,仅保留 2n 位乘积,供软件使用
- 指令分为:无符号数 与 带符号数的乘法
编译器可以使用 2n 位乘积来判断是否溢出
整数乘法溢出漏洞
int copy_array(int *array, int count) {
int i;
int *myarray = (int*)malloc(count*sizeof(int));
if(myarray = NULL)
return -1;
for(i = 0; i < count; i++)
myarray[i] = array[i];
return count;
}
这段代码的第三行,当 count 非常大,比如
乘以 4 以后得到 。结果肯定溢出了。因为,最大的数字是 。
也就是说最后的答案就是 4。这样就会产生漏洞
变量与常数之间的乘运算
整数乘法运算比移位和加法等运算所用时间长,通常一次乘法运算需要多个时钟周期,而一次移位、加法和减法等运算只要一个或更少的时钟周期,因此,编译器在处理变量与常数相乘时,往往以移位、加法和减法的组合运算来代替乘法运算
x × 20,编译器可以利用 20=16+4,将 x × 20 转换为 (x<<4)+(x<<2),这样,一次乘法转换成了两次移位和一次加法
不管是无符号数还是带符号整数的乘法,即使乘积溢出时,利用移位和加减运算组合的方式得到的结果都是和采用直接相乘的结果是一样的
除法
整数除法不会很难发生溢出,除了 ,会发生溢出外,其余的情况都不会溢出。
因为负数的个数比正数的个数多了一个。
而且!除 0 的结果无法用机器数字表示,但是浮点数就不一样了,浮点数能够用机器数表示无穷。
当整数除 0 的时候就要找操作系统来帮忙了。
变量与常数之间的除运算
对于整数除法运算,由于计算机中除法运算比较复杂,而且不能用流水线方式实现,所以一次除法运算大致需要 30 个或更多个时钟周期,比乘法指令的时间还要长!
为了缩短除法运算的时间,编译器在处理一个变量与一个 2 的幂次形式的整数相除时,常采用右移运算来实现。
- 无符号:逻辑右移
- 带符号:算术右移
除法有两种情况
-
结果一定取整数
能整除时,直接右移得到结果,移出的为全 0
-
不能整除时,采用朝零舍入,即截断方式
无符号数、带符号正整数:移出的低位直接丢弃,而对带符号的负整数,应该加偏移量(),然后再右移 k 位。
-3 / 2(假设只有 4 位存储)
- 如果没有加偏移量
-3 / 2 = 1101 >> 2 = 1110 = -2
- 如果加了偏移量
-3 / 2 = (1101 + 1) >> 2 = 1110 >> 2 = 1111 = -1
与我们期待 -1 相同