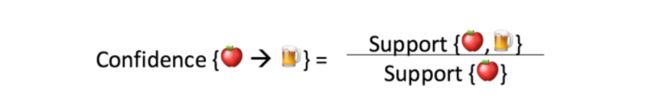笔记内容:
- association rules的简要原理及适用范围
- association rules的R实现及结果解读
- LDA topics简释,python实现及结果解读
association rules(关联规则)的简要原理及适用范围
各种association rules的教程和介绍里,总会提到超市货架摆放:有些商品总是被一起购买,也就是同时出现在同一笔交易(transaction)里。比方说洗发水和护发素,牛奶和面包等。将这些常常被同时购买的商品摆放在一起,有助于促进消费,提高营业额。
它适用于n组分类变量的组合,了解这些分类变量之间的关联是否紧密。它的input一般是n条list, 每个list里是同时出现的分类变量(items)。在超市的例子里,每个transaction就是一笔交易,当然也可以是一个患者一次就诊的所有诊断结果,处方药物名称,接受的治疗名称... ....
transaction1 a b c d
transaction2 a b c
transaction3 a e p u o y
transaction4 r b
...
量化items之间的关联有以下几个参数:
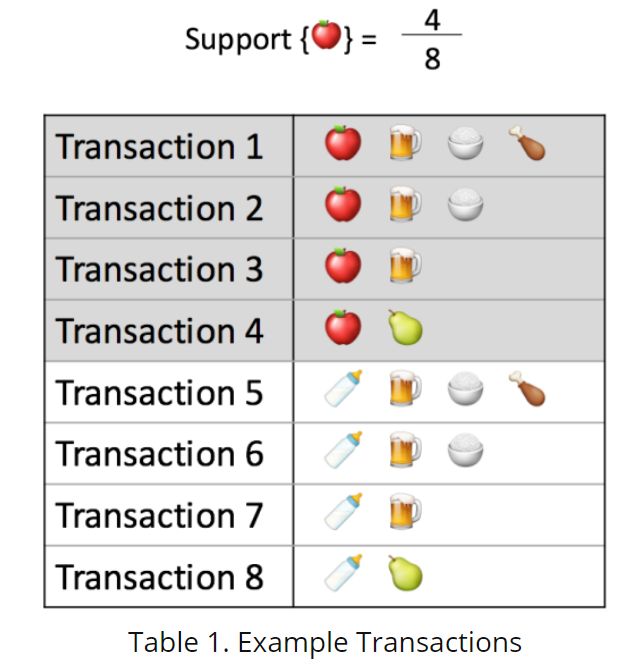
support{a,b,c..}: "How popular the items are" 一个或者多个items的组合,出现的频率。如下所示:
confidence{x -> y}: 在x出现的条件下,y也出现的可能性。显然,如果x,y调换位置,值会不一样。如下所示,support{apple,beer}是3/8, support{apple}是4/8,则confidence{apple->beer}为3/4.
lift{x -> y}: 在x出现的条件下,且在矫正了y的出现频率,y也出现的可能性,=1则表明x和y没有太大关联,<1即在x出现时,y出现的可能性小,>1为在x出现时,y出现的可能性大。如下所示,lift{apple->beer} = (3/8)/((4/8)*(6/8))=1,说明apple和beer没有什么关联。
association rules的R实现及结果解读
library(arules)
library(arulesViz)
library(htmlwidgets)
data("Groceries") #arules的自带数据集
# data <- read.transactions("xxx.csv",fromat='basket')
# 如果从本地导入一条一条的数据则如上所示
rules <- apriori(Groceries, parameter = list(support = 0.001, confidence=0.8))
# support和confidence这里为cutoff值,只选用support大于0.001及confidence大于0.8的组合(rules)
inspect(rules[1:5]) #先只看前20个rules
lhs rhs support confidence lift count
[1] {liquor,
red/blush wine} => {bottled beer} 0.001931876 0.9047619 11.235269 19
[2] {curd,
cereals} => {whole milk} 0.001016777 0.9090909 3.557863 10
[3] {yogurt,
cereals} => {whole milk} 0.001728521 0.8095238 3.168192 17
[4] {butter,
jam} => {whole milk} 0.001016777 0.8333333 3.261374 10
[5] {soups,
bottled beer} => {whole milk} 0.001118454 0.9166667 3.587512 11
plot(rules[1:15],method = 'graph',max=1000)
plot(rules[1:15],method = 'graph',engine = 'interactive', max=1000) #生成交互式图
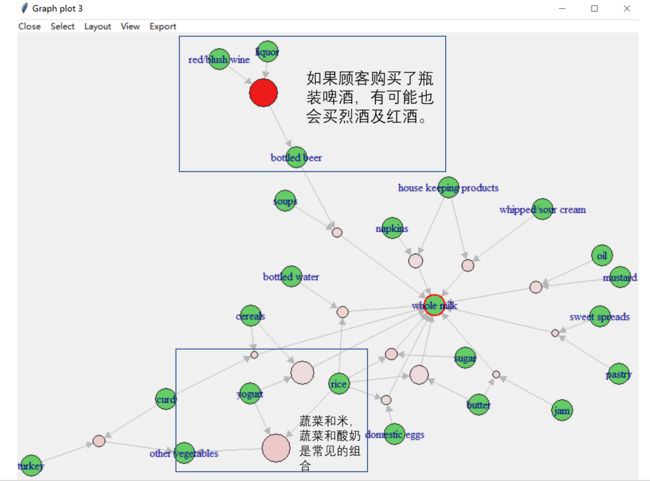
win系统上的交互式图截图如下所示:
每个绿色圆圈代表一个item。
粉色或者红色的圆圈连接两个items,代表了这两个item的关联程度。红色越深表明关联越密切(两者同时出现的可能性更高),越浅代表关联越不紧密。
粉色或者红色的圆圈大小代表了关联的support,即出现的频率。一个组合(rule)出现的频率越高,圆圈越大。
找到这些组合意义不仅仅在于发现“谁和谁更可能出现在一起”,也可能为扩展现有知识库提供线索。比方说在基于电子病历的分析中,通过研究大样本量的患者诊断结果,发现某些疾病和某些疾病更有可能同时出现在一起,可以验证现有的医学知识,也可能发现新的疾病关系谱。
LDA topics简释,python实现及结果解读
LDA(隐含迪利克雷分布,Latent Dirichlet Allocation)是一种应用于自然语言处理的主题建模技术,用于将文本转化成一系列主题,即辨别出一个文本讲了那些主题内容。和关联规则(association rules)类似。它提供的是主题分布,即各个主题出现的概率大小。它最终的output是一系列主题,每个主题中是一系列构成这个主题的“词”。
...=_=具体的原理我也不太懂,可以参考一下这篇博客。
(如果哪天我懂了就写上来)
使用gensim模块的python实现:
from gensim.corpora.dictionary import Dictionary
from gensim.models import LdaModel
from tqdm import tqdm # 用来弄一个进度条
# 比方说input是XXX.csv:
# transaction1,a,b,c,d
# transaction2,a,b,c
# transaction3,a,e,p,u,o,y
# transaction4,r,b
# ...
cases_in = []
with open("XXX.csv") as f:
for line in f:
line = line.strip('\n')
li = line.split(',')
cases_in.append(li)
mdict = Dictionary(cases_in)
mcorpus = [mdict.doc2bow(i) for i in tqdm(fever_in)]
mlda = LdaModel(mcorpus, num_topics=15, iterations=1000, id2word=mdict)
# 设置15个topics
# visualization可视化
from pyLDAvis.gensim import prepare
import pyLDAvis
vis = prepare(mlda, mcorpus, mdict)
pyLDAvis.save_html(vis, open("lda.html"),'wb'))
# 然后可以直接打开html文件在web看到可视化结果
# save topic to txt:把你得到的主题存下来
topic15 = mlda.print_topics()
# print topic15得到:
# [(0, u'0.026*"4019" + 0.017*"486" + 0.014*"2724" + 0.014*"4280" + 0.014*"51881" + 0.012*"2762" + 0.011*"25000" + 0.010*"42731" + 0.010*"3051" + 0.009*"41401"'), (1, u'0.020*"2724" + 0.019*"4...
# 是一个包含了15个topics的list,每个topic是一个tuple, 包括 (topic序号,'出现的概率*词 + 出现的概率*词...')
topic15_df = pd.DataFrame()
for tu in topic15:
indx = tu[0]
di = [i.split('*')[1].strip('"') for i in tu[1].split(' +')]
with open(os.path.join(in_dir,'XXXtopic15.csv'),'a') as f:
f.write(str(indx) + ',')
for d in di:
f.write(d + ',')
f.write('\n')
于是结果是output出你设置好的若干个topics,这些topics里有一系列词,默认出现频率最高的前10个词。比方说在电子病历分析中,这些词全部都是诊断代码,我们可以归纳出每个topic里的诊断代码是关系紧密的,可能具有共同的"topic"。对于一些topic里的诊断代码用现有医学知识不能关联在一起的,可能会为开发新的医学知识库提供线索,也可能是一些误差。需要根据具体情况分析。
参考链接:
association rules R 实现
association rules 概念参考
LDA的python实现及释义参考
gensim文档