Algorithms Part1课程第一周的Programming Assignment是Percolation问题,该问题是Union-Find算法的一个应用实例。作业要求见以下链接:http://coursera.cs.princeton.edu/algs4/assignments/percolation.html,要求用Java实现算法。此外该课程使用了作者提供的API用以简化编程,如基本输入、输出、随机数生成、数据分析等库函数,在上述链接中可直接下载。
模型描述:
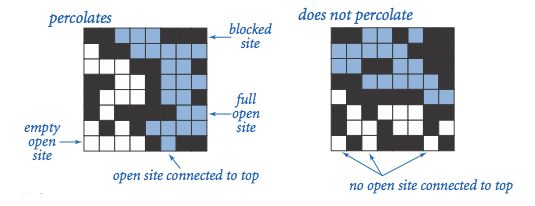
Percolation即渗透过程,其模型如下:一个方形“水槽”(system)由N*N个方格(site)组成,每个方格有开启(open)或关闭(blocked)两个状态,相邻(即上下左右)的开启格子能够构成一条同路。如果一个格子处于开启状态,并且与顶端的一行能够通过开启的格子实现连通(connected)通路,我们说这个格子处于充满水(full)的状态;如果一个“水槽”(system)的顶端格子与底部格子通过开启的格子实现了连通,我们称这个“水槽”是可以渗透(percolates)的。如下图所示:
第一章的作业需要制作两个类。第一个Percolation包含五个方法,主要是用来打开渗漏的格子。第二个类PercolationStats 同样有五个方法,用来找出N*N格子中,能够产生渗漏的阈值概率的95%置信区间。先说一下大概的想法和原理。官网上提供有这道题目的思路,就是在创建格子的过程中首先要在顶层和底层各加一层,这样的话在测试是否渗漏时直接测试(0,1)和(N+1,1)就好了首先来说下第一个类:官网的API已经写好:
public class Percolation {
public Percolation(int N) // create N-by-N grid, with all sites blocked
public void open(int i, int j) // open site (row i, column j) if it is not open already
public boolean isOpen(int i, int j) // is site (row i, column j) open?
public boolean isFull(int i, int j) // is site (row i, column j) full?
public boolean percolates() // does the system percolate?
public static void main(String[] args // test client (optional)
}
- 构造函数 Percolation
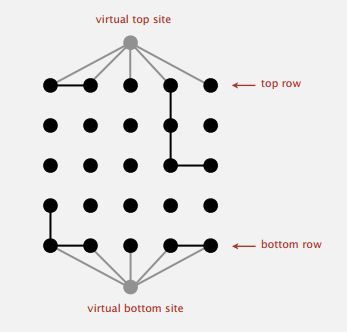
该构造方法对模型初始化,我们创建一个NN大小的一维布尔数组作为“水槽”,数组值记录每个格子的开闭状态,初始状态为关闭。此外,我们需要另一个(NN+2)大小的一维数组存储连通关系,根据Union-Find算法的学习,我们创建类型为WeightedQuickUnionUF的数组。大小之所以为(N*N+2),是因为在检查是否渗透的时候,可以通过在顶部与底部设置两个虚拟点,其与顶端或底部的一排是相连通的,这样检查是否渗透的时候,无需遍历顶部或底部一排的每一个点,只需要检查两个虚拟点是否连通即可,如下图所示:
- 打开格子方法open
检查坐标为(i, j)的点是否开启,如果没有开启,则将其开启。注意i,j的取值范围为1~N。此外,开启格子后,需要检查其上下左右的格子是否同样已经打开,如果已经打开,则通过WeightedQuickUnionUF的union()方法将两个格子连通起来;另外根据作业要求,需要首先检查是否越界,抛出java.lang.IndexOutOfBoundsException()错误; - isOpen(int i, int j):只需要返回该点的开闭状态值;
- isFull(int i, int j):检查该点是否已经打开并且已经与顶部的虚拟点(相当于顶部的一排)连通,用WeightedQuickUnionUF的connected()方法检测;
- percolates():检查顶部的虚拟点与底部的虚拟点是否连通,用WeightedQuickUnionUF的connected()方法检测;
注意:
- 加入虚拟节点。首虚拟节点与第一层所有打开的元素相关联,尾虚拟节点和最后一层所有打开的节点相关联。如果首尾虚拟节点在一个集合中,那么系统是渗透成功的。 但是也会出现一个问题(backwash),因为有一些格子虽然从上面不能渗透到,但和尾虚拟节点连接后,他们也和首虚拟节点在一个集合了。
- 使用两个并查集避免backwash。一个只负责维护首虚拟节点,当进行isFull判断是否只考虑这个并查集,另一个并查集进行首尾虚拟节点的维护,用在percolates的判断中。
- 在用一维数组模拟二维“水槽”时,我们用i,j坐标进行表示,(i, j)表示的是数组中序号为(i - 1)*N + (j - 1)的元素;此外,由于虚拟点的设置,坐标的对应容易出现混乱,需要首先考虑清楚这个问题。所以我们将数组的N初始化为N+1
package percolation; /**
* @author rxy8023
* @version 1.0 2017/6/17 22:00
*/
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.WeightedQuickUnionUF;
public class Percolation {
// number of grid should be n +1,because row and column indices are between 1 and n
private int n;
// union-find data structure
private WeightedQuickUnionUF uf;
// mark open site
// 0 for Blocked site, 1 for Open site, 2 for Open site connected to the bottom
private byte[][] open;
// number of open sites
private int num;
/**
* create n-by-n grid, with all sites blocked.
*
* @param n number of dimension
*/
public Percolation(int n) {
if (n <= 0) throw new IllegalArgumentException("Invalid input : n must > 0 !");
this.n = n + 1;
uf = new WeightedQuickUnionUF(this.n * this.n);
open = new byte[this.n][this.n];
}
public static void main(String[] args) {
In in = new In(args[0]);
int n = in.readInt();
Percolation percolation = new Percolation(n);
boolean isPercolated = false;
int count = 0;
while (!in.isEmpty()) {
int row = in.readInt();
int col = in.readInt();
if (!percolation.isOpen(row, col)) {
count++;
}
percolation.open(row, col);
isPercolated = percolation.percolates();
if (isPercolated) {
break;
}
}
StdOut.println(count + " open sites");
if (isPercolated) {
StdOut.println("percolates");
} else {
StdOut.println("does not percolate");
}
}
/**
* Validate the row and col indices.
*
* @param row row index
* @param col col index
*/
private void validate(int row, int col) {
if (row <= 0 || row >= n) {
throw new IndexOutOfBoundsException("Invalid input : row index out of bounds !");
}
if (col <= 0 || row >= n) {
throw new IndexOutOfBoundsException("Invalid input : col index out of bounds !");
}
}
/**
* open site (row, col) if it is not open already
*
* @param row the index of row
* @param col the index of column
*/
public void open(int row, int col) {
validate(row, col);
// is open already
if (isOpen(row, col)) return;
// make this site open
open[row][col] = 1;
num++;
// we make 0 represent the virtual-top, 1 represent the virtual-bottom.
// is the bottom row
if (row == n -1) open[row][col] = 2;
// is the top row
if (row == 1) {
uf.union(0, row * n + col);
// 1-by-1 grid corner case
if (open[row][col] == 2) open[0][0] = 2;
}
// above site is open
if (row - 1 > 0 && isOpen(row - 1, col)) {
update(row - 1, col, row, col);
}
// below site is open
if (row + 1 < n && isOpen(row + 1, col)) {
update(row + 1, col, row, col);
}
// left site is open
if (col - 1 > 0 && isOpen(row, col - 1)) {
update(row, col - 1, row, col);
}
// right site is open
if (col + 1 < n && isOpen(row, col + 1)) {
update(row, col + 1, row, col);
}
}
/**
* update components: connect the opened site to all of its adjacent open sites
*
* @param i1 adjacent open site row index
* @param j1 adjacent open site col index
* @param i2 the opened site row index
* @param j2 the opened site col index
*/
private void update(int i1, int j1, int i2, int j2) {
int p = uf.find(i1 * n + j1);
int q = uf.find(i2 * n + j2);
uf.union(i1 * n + j1, i2 * n + j2);
// if one of them is connected to bottom, then the updated component is connected to bottom too.
if (open[p / n][p % n] == 2 || open[q / n][q % n] == 2) {
int t = uf.find(i2 * n + j2);
open[t / n][t % n] = 2;
}
}
/**
* is site (row, col) open?
*
* @param row row index
* @param col col index
* @return
*/
public boolean isOpen(int row, int col) {
validate(row, col);
return open[row][col] > 0;
}
/**
* is site (row, col) full?
*
* @param row row index
* @param col col index
* @return
*/
public boolean isFull(int row, int col) {
validate(row, col);
return open[row][col] > 0 && uf.connected(0, row * n + col);
}
/**
* number of open sites
*
* @return
*/
public int numberOfOpenSites() {
return num;
}
/**
* does the system percolate?
*
* @return
*/
public boolean percolates() {
int root = uf.find(0);
return open[root / n][root % n] == 2;
}
}
蒙特卡洛仿真分析(PercolationStats类)
用蒙特卡洛(Monte Carlo)方法进行仿真分析,确定渗透阈值p,具体方法是:
初始化将所有N*N个格子置于关闭状态;
每次随机选择一个格子进行开启操作,直到系统达到渗透状态;
统计此时开启的格子数,与全部格子数相比计算一个p值的样本;
独立重复T次上述实验,最后计算出T个p值的样本,记为x1,x2……xT。
进行以下统计操作。
按照下式计算均值与方差:
假设T值足够大(至少30次),则可以根据下式计算置信区间在95%的的渗透阈值范围:
package percolation;
import edu.princeton.cs.algs4.StdOut;
import edu.princeton.cs.algs4.StdRandom;
import edu.princeton.cs.algs4.StdStats;
/**
* @author rxy8023
* @version 1.0 2017/6/17 22:00
*/
public class PercolationStats {
// sample mean of percolation threshold
private double mean;
// sample standard deviation of percolation threshold
private double stddev;
// low endpoint of 95% confidence interval
private double confidenceLo;
// high endpoint of 95% confidence interval
private double confidenceHi;
// est[i] = estimate of percolation threshold in perc[i]
private double[] est;
/**
* perform trials independent experiments on an n-by-n grid
*
* @param n
* @param trials
*/
public PercolationStats(int n, int trials) {
if (n <= 0 || trials <= 0) throw new IllegalArgumentException("Invalid input : n or trials musu > 0 !");
est = new double[trials];
for (int k = 0; k < trials; k++) {
Percolation perc = new Percolation(n);
double count = 0;
while (!perc.percolates()) {
int i = StdRandom.uniform(1, n + 1);
int j = StdRandom.uniform(1, n + 1);
if (perc.isOpen(i, j)) continue;
perc.open(i, j);
count++;
}
est[k] = count / (n * n);
}
mean = StdStats.mean(est);
stddev = StdStats.stddev(est);
confidenceLo = mean - (1.96 * stddev) / Math.sqrt(trials);
confidenceHi = mean + (1.96 * stddev) / Math.sqrt(trials);
}
public static void main(String[] args) {
int n = Integer.parseInt(args[0]);
int t = Integer.parseInt(args[1]);
PercolationStats stats = new PercolationStats(n, t);
StdOut.println("mean = " + stats.mean());
StdOut.println("stddev = " + stats.stddev());
StdOut.println("95% confidence interval = " + stats.confidenceLo()
+ ", " + stats.confidenceHi());
}
/**
* Get sample mean of percolation threshold
*
* @return
*/
public double mean() {
return mean;
}
/**
* Get sample standard deviation of percolation threshold
*
* @return
*/
public double stddev() {
return stddev;
}
/**
* Get low endpoint of 95% confidence interval
*
* @return
*/
public double confidenceLo() {
return confidenceLo;
}
/**
* Get high endpoint of 95% confidence interval
*
* @return
*/
public double confidenceHi() {
return confidenceHi;
}
}
总结:
如何根据API编译JAVA程序:
1.把API所需要做的内容全都用文字详细写出来,每个步骤该做什么;
2.可以写出伪代码,类似于算法课上所要求的,详尽写出;
3.选好数据结构,简单变成不需要;
4.Coding