2/17
这章一开始,作者先讲了数学研究的有趣的方法:几何化。这是一个非常重要的数学思想,数形结合也是高中数学的重头戏,我到现在都记得书上讲到这块引用的华罗庚的一句话:“数缺几何少直观,几何缺数少精确”,直观的表示一些量的关系,就是几何图形的优势。
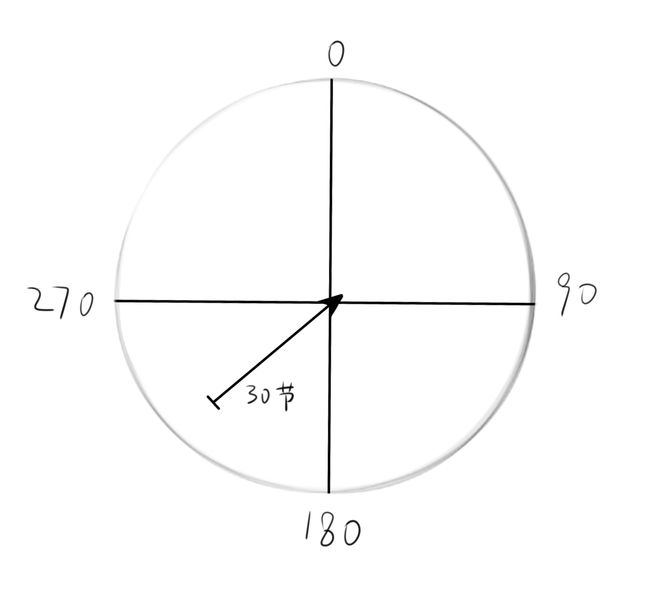
当然书中讲的几何化也不是简单的函数图形,而是更加广义上的数学上的几何化:把各类研究对象抽象成点、线、面。举个简单例子:比如你是一个飞行员,在高空中知道风向和风速很重要,那么像下图那样的风向仪图形显示就可以直观的表示出这两个量。这里线条长短表示风速大小,箭头指向表示风向,换句话说这其实就是“又有大小又有方向”的向量了。
如果你还想了解气温对风的改变,并且要显示在一张图上,那么你就需要一个三维的图,建立一个新的坐标来表示三个变量。这样的三维几何模型很容易想象,但是要把它画在一个二维的纸上是不可能的,我们只能把他的一个二维投影画下来。如果还想表示更多的量,比如气压,湿度,那么就需要4维,5维等等。“也许你觉得看不见的维度几何直观化是不显示的,因为据说那些声称‘能看见四维空间’的人都关在疯人院里。那么4、5维空间的几何化也就是不现实的吗?”事实上,几何化表示4、5……甚至无穷维是数学家或其他科学家的家常便饭,诀窍就是把这些高维几何图在2维或3维的投影画出来就可以研究高维的情况,或者记住几条描述高维物体的几何化法则,就可以研究了。
这么说来,基本上所有的事物在数学处理下,都可以变成直观形象的几何图形(But,事实就是高考题里面最坑爹的就是考察读图识图能力的题,在出题老师的各种费尽心机的变形和遮掩下原本应该直观表示变量的图形都变得遮遮掩掩含糊不清或者暗藏巨大的误导,这时候图像的直观性要么完全体现不出来,要么完全是“直观的误导”,实在是让人头疼。。。)。作者在这一章讲解奇怪吸引子就要用到几何化的直观表述,然而就像我前面吐槽的高考题那样,这些“直观表述”其实,有点难理解。。。
2/18
书中接下来的内容都十分的深涩难懂,因为这确实是一个全新的领域,而且作者在讲解的时候,可能是为了不增加阅读难度,略去了很多数学过程(我敢肯定这些数学证明写上了我也看不懂),所以思路读起来非常的跳脱。又有不少的数学证明和理论,所以基本没办法完全理解。我只能尝试的讲一些,当作对这个概念有点印象吧。。。
我们开始用数学的几何化语言来表述上一章讲过的“模态”。模态就是一种振动,我们先来看一个在一维线条上来回振动的质点,这歌简单的模态几何化的直观表现就是下图1。图中线是质点运动轨迹所在的直线位置,而粗一点的线段就是轨迹来回运动的距离(显然运动轨迹和所在直线是重叠在一条线上的,应该没有粗细之分,画粗一点是为了显示出来),这是该运动在空间位置上的表示。而在很久之前的一章我们介绍过描述一个物体的运动不止要知道它的位置,还要知道速度,我们也把速度的大小变化几何化,就是图2一样的环。我们来解释一下这个“速度环”,因为速度是有方向的,所以坐标中横坐标轴上方的速度方向为正(这个正的方向其实可以自己规定,但是只要规定好之后以后都按照这个为参考。这里我就规定图1中向右为速度正方向),即向右,而横坐标下方速度为负,这意思不是说速度的大小是负,而是表示速度的方向为负,即向左。在这里正负只表示方向而非大小。图2结合图1就能描述这个支点的一维振动了:当支点从点A运动到点B,速度先增大后减小,在AB中点处速度最大;过了AB中点后质点减速,到B后速度大小减为零,然后质点速度反向,再从B运动到A,速度的大小变化和从A到B一样。这个运动过程就这样循环往复,形成周期运动,表现出来就是质点振动,即“模态”。
2/19
接下来是作者要讲到的重要内容:奇怪吸引子。作为研究湍流的理论,我们自然要回到对流体的讨论。一个流体中有无数个运动质点(可以把每一个水分子都看成一个运动质点),所以我们需要无穷维空间来几何化表述这个流体中所有质点的空间和速度。
。。。今天就先更新到这里。。。唔唔唔。。。我知道字数很少因为我实在看不懂。。。所以上网查了一下这个。。。
我在网上找到了很有意思的东西!用数学模拟软件把奇怪吸引子投影到三维空间,就可以成为很有艺术感的东西!不过这玩意做出来估计很复杂。。。
网页:http://www.cnblogs.com/WhyEngine/p/4359269.html
更原本的网页:http://chaoticatmospheres.com/mathrules-strange-attractors PS:这好像是一个科学艺术品的网页,里面很多有意思的东西,只是都是英文完全。。。看不懂。。。
还有科学家基于这个玩意编写了一段音乐,迷之好听~【音乐文件下载见:http://www.360doc.com/content/13/0608/15/11566744_291512213.shtml 】
2/20
又一次水更新。。。
接着干正事。昨天上面那一小段讲到描述流体需要无穷维的空间放置质点,所以最后对这个体系描述的时候,我们只能观测这个系统在2、3的投影。(投影这个概念很好理解,对于一个3维的立方体,观测它在2维的情况就类似用一束平行光去照射这个立方体,用一张纸【2维平面】去接这个影子,接出来的方形影子就是在2维观测的三维立方体的投影)把一个高纬度的东西投影到2维,就是一个平面,投到3维,就是一个立体图形。
2/25
时隔许久的更新。。。
在讨论流体状态的时候,只考虑流体的长期状态,对于一些不一样的暂态(比如水龙头刚打开的那一瞬)忽略掉。然后我们就要开始讨论这个湍流的几何化模型了。
图10.4(a)表示的是一个流体的定常状态,点P是这个系统在2维的一个投影,点P静止不动也就说明这个系统没有表现出周期运动,而是我们之前说过的定常状态。图10.4(b)则就是流体的周期振荡,系统(点P)的运动形态是循环周期的。这之后为了方便理解,我们可以用一点数学家的小伎俩:非线性坐标变换来让这个运动几何表示的轨道变成正圆。所谓非线性坐标变换就像是透过变形的玻璃看一幅画一样,画本身没有改变, 我们看到的结果却不一样了。
有了这些铺垫,我们就“具有了将几个模态叠加形象化所需要的所有思想了”。像图10.5就是P的运动湍流系统在不同角度的投影下产生的圆周,角速度的不同表示周期不同,而在投影前的无穷维中这些模态运动都是叠加在一起的。
像这样:一个无穷维(这里只用了3维投影代替)的湍流吸引子在不同情况下投影出来的运动状态不一样。每个状态对应着原来湍流中的一种模态。
不过这是我自己的理解,不一定对。。。
3/3
时隔许久的一次更新。今天是周末,来一次小更新,以后都会类似这样吧,周末来一次更新。开学后事情会越来越多,而且这本书后面胡越来越难,更新速度会慢的可怕。。。
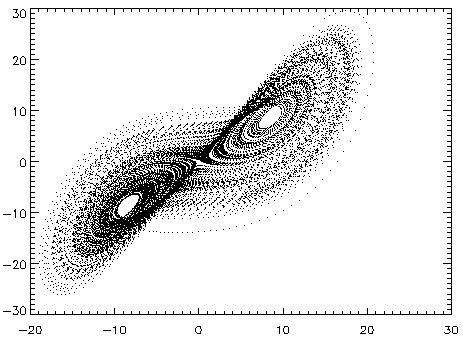
上次讲到把一个无穷维的奇怪吸引子结合非线性坐标变换以不同投影方式得到了不少几何化表示。现在我们来看这个图,是一个三维空间中时间演化的透视图,这种运动称之为“洛伦茨吸引子”。洛伦茨(Edward Lorenz)是美国气象学家,和电磁学里面那位洛伦兹(Antoon Lorentz)不是一个人哦。这个洛伦茨吸引子是这位气象学家在研究大气环流的时候采用的一种近似的描述方式。大气环流如湍流一样,也应该近似的用无穷维的空间来放置那无穷多个质点,但是洛伦茨通过粗略的估计,用一个能在计算机上三维表示的“洛伦茨吸引子”(一个时间演化)正确的代替了无穷维空间中的时间演化。计算机产生的结果就是这个图显示的。
这里先撇开书,讲一些我在网上看到的有趣的东西。洛伦茨,就是提出“蝴蝶效应”的气象学家。这个过程很有意思,他想要检验计算机模拟预测天气的准确性,于是就试着在计算机里输入了两组差别很小的初始数据,抱着好奇的心态想要看看这两组数据之后的拟合会有什么区别。有故事说是他去喝了杯茶什么的吧,当他回来看这两组数据的时候,就出现:“震惊!两组相差极小的初始数据揭露了惊天秘密!(用一下UC题/斜眼笑)”,两组数据的拟合函数曲线在不久之后就完全的分道扬镳,差别越来越大。这也就告示着天气预报的准确预测是很难的,因为极小的差别就能产生巨大的差别,也就是我们之前说的初条件敏感依赖性。
洛伦茨在他的学术报告中用了一个比喻:“一个气象学家提及,如果这个理论被证明正确,一只海鸥扇动翅膀足以永远改变天气变化。”后来,他用电脑模拟出这种情况的图像(也就是上面说的洛伦茨吸引子),发现外形和蝴蝶很相像(见下图),于是就把这个比喻改成了现在我们熟知的“蝴蝶效应——一只南美洲亚马逊河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,可以在两周以后引起美国得克萨斯州的一场龙卷风。”。蝴蝶效应,就是混沌最初的认识。
Tbc……