在描述堆之前先看看一道思考题先,假设现在要求设计一种数据结果,用来存放整数,要求提供3个接口:
1.添加元素;2.获取最大值;3.删除最大值
你考虑可能有如下几种:
动态数组或者双向链表:
有序动态数组或者双向链表
BST
复杂度分析
但是有没有更优的数据结构呢?
可以考虑用堆去实现,堆获取最大值O(1),删除最大值:O(logn),添加元素O(logn)
另外注明的Top k问题也是可以用数据结构堆来解决的
堆(Heap)
堆是一种树状的数据结构(不要跟内存模型中的堆空间混淆),常见的堆实现有:
二叉堆(Binary Heap,完全二叉堆),多叉堆(D-heap,D-ary Heap)
索引堆(Index Heap),;二项堆(Binomial Heap) 斐波那契堆(Fibonacci Heap)等
堆有一个重要的性质:任意节点的值总是或者子节点的值
如果任意节点的值总是子节点的值,称为:最大堆,大根堆,大顶堆;如果任意节点的值总是子节点的值,称为:最小堆,小根堆,小顶堆
堆的基本接口设计
int size();//元素的数量
boolean isEmpty();//是否为空
void clear();//清空
void add(E element); //添加元素
E get();//获得对顶元素
E remove();//删除对顶元素
E replace(E element);// 删除堆顶元素的同时插入一个新元素
二叉堆(Binary Heap)
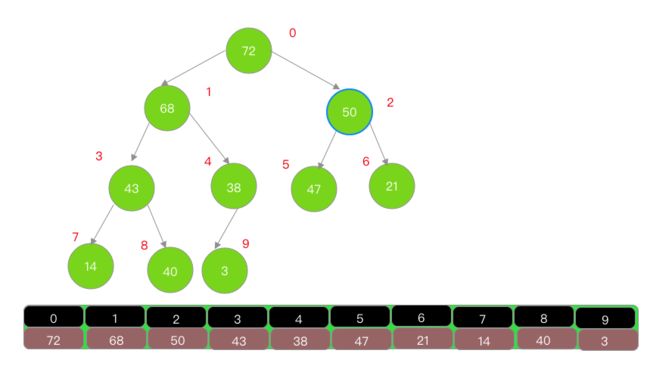
二叉堆的逻辑结构就是一颗完全二叉树,所以也叫完全二叉堆,鉴于完全二叉树的一些特性,二叉堆的底层(物理结构)一般用数组实现即可;
索引i的规律(n 是元素数量)
如果i=0,那么它是根节点;
如果i > 0,它的父节点的索引为floor((i - 1)/2);
如果2i + 1 n - 1,它的左子节点的索引为2i + 1;
如果2i + 1 > n - 1,它无子节点;
如果2i + 2 n -1,它的右子节点的索引为2i + 2;
如果2i + 2 > n -1 ,它无右子节点
从上面的图可以看出,获取二叉堆的最大值非常简单
最大值获取
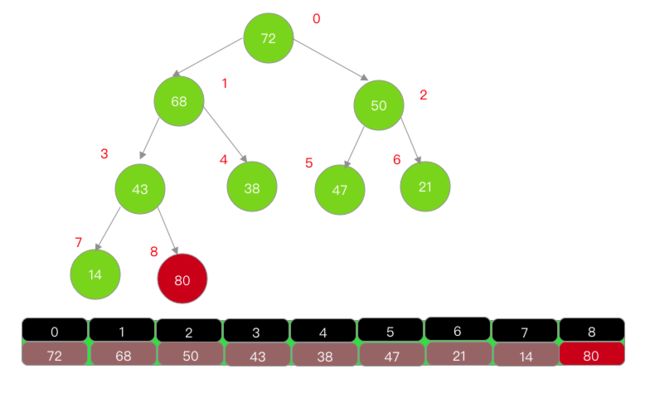
元素添加(最大堆元素添加)
示例图如下:
添加总结
循环执行操作,例如上图的80,如果node > 父节点(与父节点交换位置);如果node 父节点,或者node没有父节点(退出循环),时间复杂度是O(logn)
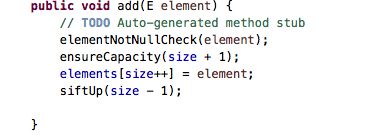
源码示例图:
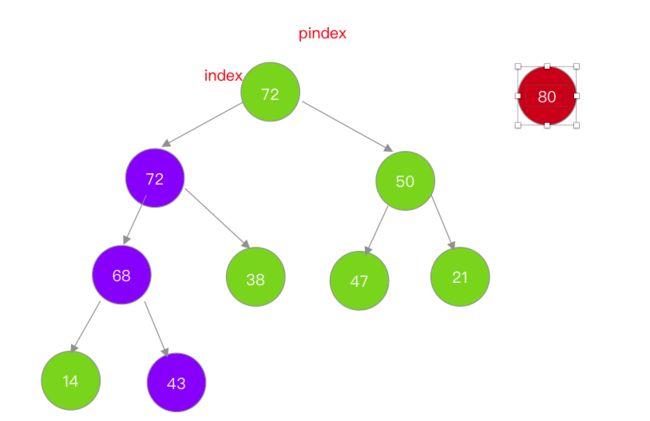
可以看到shiftup方法实现有两个,第一个方法就是对应着前面展示的示例提图,这种情况复杂度大概是3 * O(logn),因为有3次交换,而方法2对应的是下面的展示图,复杂度可以优化到1 * O(logn) + 1
方法二相对于方法一的不同就是方法二在记录着最终需要赋值元素的索引,跳出外循环之后才赋值,这也是优化的关键点所在;到这里添加元素就讲完了,接下来看看删除。
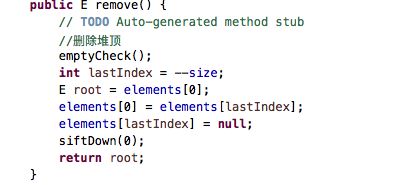
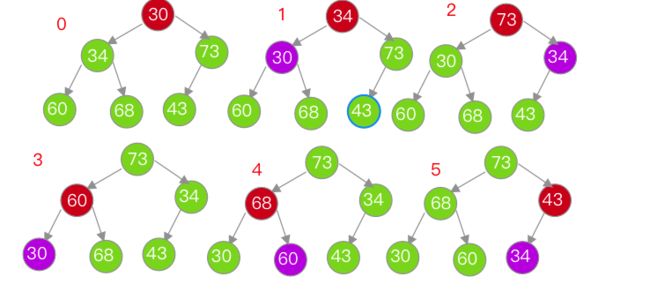
最大堆删除
示例图:
最大堆删除总结
1.用最后一个节点去覆盖根节点
2.删除最后一个节点
3.循环执行以下操作(图中的43简称为node),如果node < 最大的子节点,与最大的子节点交换位置,如果node最大的子节点,或者node没有子节点,退出循环;
这个过程叫做下滤(Sift Down),时间复杂度:O(logn)
删除代码图:
最大堆-批量建堆(Heapify)
有两种方法:1.自上而下的上滤;2.自下而上的下滤
1.自上而下的上滤
2.自下而上的下滤
代码实现图:
最大堆-批量建堆-效率对比
所有节点的深度之和
仅仅是叶子节点,就有近n/2个,而且每一个叶子节点的深度都是O(logn)级别的,因此在叶子这一块就达到了O(nlogn)级别,O(nlogn)的时间复杂度足以利用排序算法对所有节点进行全排序
所有节点的高度之和
假设是满树,节点总个数为n,数高为h,那么n = - 1,假设所有节点的树高之和H(n) = *(h-0) + *(h-1)+......*[h-(h-1)];
H(n) = h * ()-[1* + 2 * + (h-1)*)];
H(n)=h* -[(h-2)*+2];
H(n)=h*-h-h*+-2;
H(n)=-h -2=2*(-1)-h=2n- = O(n);
公式推导过程:
S(h)=1*2^1+2*2^2+3*2^3+....+(h-2)*2^(h-2) + (h-1)*2^(h-1)
2S(h)=1*2^2+2*2^3+3*2^4+....+(h-2)*2^(h-1) + (h-1)*2^h
S(h)-2S(h)=[2^1+2^2+2^3+...2^(h-1)]-(h-1)*2^h=(2^h-2)-(h-1)*2^h
S(h)=(h-1)*2^h-(2^h-2)=(h-2)*2^h+2;
Top K问题
从n个整数中,找出最大的前k个数(k远远小于n),如果使用排序算法进行全排序,需要O(nlogn)的时间复杂度,但是如果使用二叉堆来解决的话,可以使用O(nlogk)的时间复杂度来解决
1.新建一个小顶堆
2.扫描n个整数,先将遍历到前k个数组放入堆中,从第k+1个数开始,如果大于堆顶元素,就使用replace操作(删除堆顶元素,将k+1个数添加到堆中),扫描完毕后,堆中剩下的就是最大的前k个数
如果是找出最小的前k个数呢?
使用大顶堆,如果小于堆顶元素,就使用replace操作
demo
到这里,二叉堆介绍完毕,如果有问题,欢迎留言哈!