三、绘制圆
圆的方程可以描述为( x - x0 )2 + ( y - y0 )2= r2 ,其中 ( x0, y0) 为圆心,r为圆的半径。为了简化问题,我们假设圆心就在坐标中心(0, 0),那么
( x0, y0 )= ( 0, 0 ),那么圆的方程为:x2 + y2= r2 。
圆心不在坐标原点时,只需要做简单的平移即可。
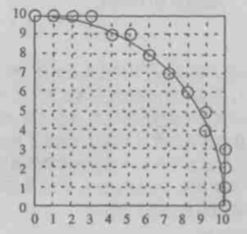
如上图所示,圆心处于坐标原点处,此时圆具有四条对称轴:
①x = 0、②y = 0、③x = y、④x = -y
这四条对称轴将整个圆分成了八段圆弧,设圆上一点( x, y ),其对称点分别为:
( x, -y )、( -x, y )、( -x, -y ) 、( y, x )、( y, -x )、( -y, x )、( -y, -x )
这叫做圆的八分对称性。只要我们画出八段圆弧中的一段,其余七段可利用八分对称性进行变化得到。
(一)中点画圆法
我们首先画第一段圆弧,草图如下所示,从点( 0, 0 )到( ri, ri )圆弧与线段P1P2相交于一点,M点为线段P1P2中点,假设当前点为Pi( xi, yi),由于每次步进一个像素,因此,
M点坐标为( xi + 1, yi– 0.5 ),P1点坐标为( xi + 1, yi),P2点坐标为( xi+ 1, yi+ 1 )。
从图上我们可以知道,下一个坐标点要么是P1,要么是P2,到底哪个点离圆弧最近,线段中点M点在圆弧与线段交点的Y坐标情况。
设圆的判别函数为:
F( x, y ) = x2 + y2 -r
我们知道,对于圆上任何一点F( x, y ) = 0,圆外的一点F( x, y ) > 0,圆内的一点F( x, y ) < 0。
我们将M点的坐标代入,如果F( xi+ 1, yi–0.5 ) < 0,说明M点在圆内,下一个点为P2,因为它离圆弧最近。如果F(xi+ 1, yi–0.5 ) > 0,说明M点在圆外,下一个点为P1,因为它离圆弧最近。设
di= F(xi+1, yi– 0.5)= (xi+1)2+ (yi– 0.5)2– r2
①若di < 0,则取P1为下一个点,即
xi+1 = xi + 1
yi+1 = yi
此时P1的下一个点的判别式为:
di+1= F(xi+ 2, yi– 0.5)= (xi+ 2)2+ (yi–0.5)2– r2
展开后将di带入可得到判别式的递推关系:
di+1 = di + 2xi+ 3
②若di > 0,则取P2为下一个点,即
xi+1 = xi + 1
yi+1 = yi – 1
此时P2的下一个点的判别式为:
di+1 = F(xi+ 2, yi– 1.5)= (xi+ 2)2+ (yi–1.5)2– r2
展开后将di带入可得到判别式的递推关系:
di+1 = di + 2(xi- yi) + 5
③在第一个象限的第一个点(0, R)时,即当i=0,x0=0,y0=r,判别式d的初始值d0:
d0= F(1, r – 0.5) = 1 – (r– 0.5)2– r2= 1.25 - r
我们对上面的推导加以整理,可以得出:对于(0, R)至( ri, ri)的圆弧,
x0 = 0,y0=r,d0= 1.25 - r
当di < 0,
xi+1= xi + 1
yi+1= yi
di+1 = di + 2xi+ 3
否则,di > 0
xi+1= xi + 1
yi+1= yi – 1
di+1 = di + 2(xi- yi)+ 5
设圆心坐标为( ∆x, ∆y ),那么相当于对圆心在坐标原点的圆进行平移( ∆x, ∆y ),设原坐标为( x, y ),与偏移后的坐标( X, Y )满足如下关系:
X = x +∆x,Y = y + ∆y
同时,其它七段圆弧满足对称关系,也可以很容易得出:
( X, -Y )、( -X, Y)、( -X, -Y ) 、( Y, X )、( Y, -X )、( -Y, X )、( -Y, -X )
上面计算判别时使用了浮点数,即d0= 1.25 – r,因此我们需要做进一步优化。
(二)Bresenham画圆法
Bresenham画圆法主要针对中点画圆法进行了改进,将d的计算放大两倍,同时将初始值改成3–2r,这样避免了浮点运算,乘二运算也可以用移位快速代替,采用3–2r为初始值的改进算法。还有一种方法是将d的初始值由1.25–r改成1–r,考虑到圆的半径r总是大于2(像素的最小单位是1),因此这个修改不会影响d的初始值的符号,同时可以避免浮点运算。
根据Bresenham算法,将d放大两倍,可得到:
x0 = 0,y0=r,d0= 3 - 2r
当di < 0,
xi+1= xi + 1
yi+1= yi
di+1 = di + 4xi+ 6
否则,di > 0
xi+1= xi + 1
yi+1= yi – 1
di+1 = di + 4(xi- yi)+ 10
(三)正负判定画圆法
在上述画法中,主要的判断依据是哪个点距离圆弧近。在像素的世界里,一个一个点将整个平面切分成了离散的网格,这些像素点要么在圆弧内,要么在圆弧外,要么在圆弧上。无论在哪,始终都是聚集在圆弧的附近,而且尽可能的近。之前的分析中我们知道,已知当前一点Pi( xi, yi),那么下一个点可选位置有两个:P1 ( xi+1, yi)或者P2 (xi+1, yi+1)。为了确保每个点“始终都是聚集在圆弧的附近”,我们采用一种修正的方式,即:如果当前点Pi在圆内,说明当前向着圆心的方向远离了圆弧,为了修正,那么下一个点就应该选取背离圆心方向的点;如果当前点Pi在圆外,说明当前背离圆心的方向远离了圆弧,为了修正,那么下一个点就应该选取向着圆心方向的点。因此,我们可以看出,每次在选取点的时候,都是对当前点的一种修正,修正量为1个单位,要么在Y方向,要么在X方向。如下图所示:
具体的实现方式,将当前点Pi( xi, yi)代入判别式,
①当F(xi, yi)≤ 0,
取xi+1 = xi+1,yi+1= yi。即向右走一步,从圆内走向圆外。对应图(a)中的从Pi到Pi+1。
F(xi+1, yi+1)= F(xi+1,yi) = (xi+1)2+yi2-R2 = (xi2+yi2-R2)+2xi+1 = F(xi,yi)+2xi+1
②当F(xi, yi)> 0,
取xi+1 = xi,yi+1= yi- 1。即向下走一步,从圆外走向圆内。对应图(b)中的从Pi到Pi+1。
F(xi+1, yi+1)= F(xi,yi-1) = xi2+(yi-1)2 - R2 = (xi2+yi2-R2) - 2yi + 1 = F(xi,yi) - 2yi+1
对上面分析进行整理,得到
x0 = 0,y0=r,d0= 0
当di ≤ 0,
xi+1= xi + 1
yi+1= yi
di+1 = di + 2xi+ 1
否则,di > 0
xi+1= xi
yi+1= yi – 1
di+1 = di- 2yi + 1
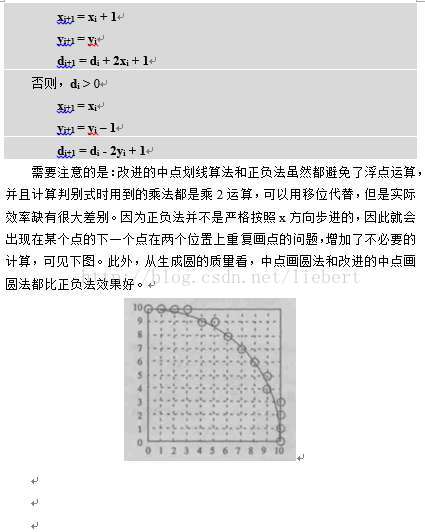
需要注意的是:改进的中点划线算法和正负法虽然都避免了浮点运算,并且计算判别式时用到的乘法都是乘2运算,可以用移位代替,但是实际效率缺有很大差别。因为正负法并不是严格按照x方向步进的,因此就会出现在某个点的下一个点在两个位置上重复画点的问题,增加了不必要的计算,可见下图。此外,从生成圆的质量看,中点画圆法和改进的中点画圆法都比正负法效果好。
防止格式错误,下面是排好版的图片: