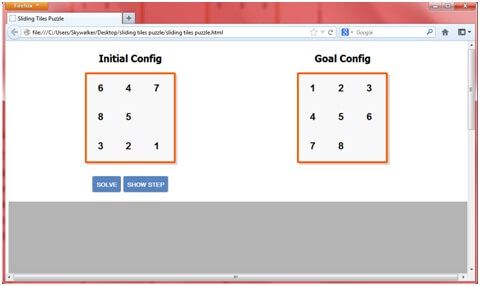
本文翻译自 JavaScript AI For An HTML Sliding Tiles Puzzle By Arnaldo Perez Castano 。
Sam Loud (1841 - 1911) 美国国际象棋手,智力游戏设计师,在1870年代发明了数字推盘游戏。这个游戏由 m 行 n 列的网格组成,每个格子可以是任何有规律的事物,比如数字,字母,图片等。
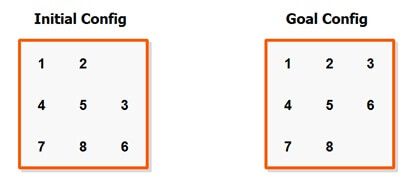
游戏的解答过程是将一个排布变成另一个排布,即从初始状态到目标状态。重新排序的方式是将空的格子和它边上的格子通过上下左右四个方向的交换来完成的。
空的格子不能被移除出边框,因此如果它在第一列的话,空格不能往左移动;如果它在最右边的一列的话,它就不能再往右移动了。行的规定也是类似的。解的过程是这样的:
这是开局。
这样就算解出了。
只要验证左边的排布和右边的目标排布是一样的就可以判断是否完成了。
本文将分两个部分。第一部分会简要解释怎么编写一个推盘游戏,用 html, css 实现显示部分,然后用 javascript 来移动盘上的滑块。这部分同时也用在下一部分的文章中。
文章的第二部分,我们会用 A* 算法来开发一个人工智能,用来解决推盘游戏,计算解答游戏的最小步数。A* 算法的多种启发式会给寻找解法带来很多帮助,启发式越智能,那么就能越快找到最优解法。启发式会按照智能程度由低到高,因此最后的启发式将是最强大的。
布局
首先我们创建一个空项目,包含一个 html 文件和一个 css 文件。分别是: index.html 和 index.css 。
引入 jquery.js 为了让生活更美好,写出更加简洁优雅的代码。(译者注:此处的文件名按照本人习惯稍作改动)
html 文件的头部如下:
Sliding Tiles Puzzle
为了页面的性能,我们把 js 都放在页面底端。这是常见的做法,因为页面渲染是由上至下的,我们希望页面上的元素先显示,因此把用来交互的 js 文件放在页面最下方。
priority-queue.js, hash-table.js, hash-set.js 是用来编写人工智能的,分别是用来存放队列,哈希表和哈希对的。
现在我们开始写 html 上的布局。首先,布局的框架是这样的。
container 容器这个类选择器在 index.css 文件中是这样的
/*
Developed by Arnaldo Perez Castano
[email protected]
*/
.container {
width: 1024px;
margin-left: auto;
margin-right: auto;
min-height: 380px;
}
面板是在页面上打印显示人工智能的日志和结果的。
.panel {
width: 100%;
background-color: rgb(180, 180, 180);
min-height: 1000px;
color: white;
font-weight: bold;
padding: 5px;
font-family: Arial;
}
我们希望容器在页面中间,所以需要给它设置宽度,并且把它的 margin-left 和 margin-right 设置为 auto。
现在我们在 container 中加入 grid-container ,用来显示推盘的网格。
Initial Config
grid-container 和它下面的元素的样式如下所示。
.grid-container {
float: left;
height: 250px;
text-align: center;
width: 50%;
}
.grid-container h2 {
font-family: Tahoma;
}
我们把推盘容器左浮动,因为两个同样的容器要显示在一行,一个是用来显示初始布局的,另一个是用来显示目标布局的。
最后,我们的推盘是这个样子的。
Initial Config
6
4
7
8
5
3
2
1
推盘游戏有三行,每行有三个滑块,这就组成了整个推盘网格。于是我们使用了以上布局,三个行容器,每个行容器有三个子元素,每个子元素是一个滑块。
为了编程方便,我们在每个子元素上添加了 data-pos 这个属性,为了记录每个滑块在推盘中的位置。 start 这个类名是为了区分初始布局的推盘和目标布局的推盘,后者不会绑定用户操作。以上几个类的样式如下。
.grid {
background-color: rgb(248, 248, 248);
border: solid 5px rgb(249, 90, 0);
width: 210px;
height: 210px;
margin-left: auto;
margin-right: auto;
border-radius: 3px;
box-shadow: 5px 5px #d8d8d8, 5px 5px #d8d8d8;
overflow: auto;
}
.row {
height: 33.3%;
}
.cell {
width: 33.3%;
height: 100%;
float: left;
text-align: center;
font-size: 150%;
font-family: Arial;
font-weight: bold;
position: relative;
}
.cell:hover {
background-color: rgb(221, 221, 221);
}
.cell span {
display: block;
transform: translateY(70%);
}
最后结果如下
接下来我们把目标布局放上去,我们复制一下起始布局,把上面的 start 改成 goal 就行了。
Goal Config
1
2
3
4
5
6
7
8
最后,我们把 Solve 和 Show Step 这两个按钮加到第一个布局的容器中。
第一个按钮会执行自动计算,也就是 A* 算法。第二个按钮会显示自动计算的一步。所以,按第二个按钮多次之后我们就得到这个推盘游戏的最优解法了。
我们已经把所有界面展示部分完成了,那么我们开始写一些功能模块的部分。我们现在要让这个游戏能动起来,其实就是要让空白的滑块能够在整个推盘中移动。我们用 javascript 来实现这个功能。 index.js 文件的前几行如下:
/*
Developed by Arnaldo Perez Castano
[email protected]
*/
var emptytilePosRow = 1;
var emptytilePosCol = 2;
var cellDisplacement = '69px';
emptytilePosRow 和 emptytilePosCol 这两个变量会保存空白滑块所处的位置。每次移动的时候,都会改变。
cellDisplacement 这个变量用来记录这个滑块在动画执行过程中所移动的距离。cell 这个类所在的 div 的 position 是 relative 。所以我们用 top 和 right 这两个属性来实现动画效果。 cellDisplacement 变量会记录下 top 和 right 的最新的值,来实现滑块的移动。
用来实现移动的方法如下:
var moveTile = function (e) {
// Gets the position of the current element
var pos = $(this).attr('data-pos');
var posRow = parseInt(pos.split(',')[0]);
var posCol = parseInt(pos.split(',')[1]);
// ...
};
请看,我们已经用上 jquery 来选择元素了。还要注意我们要用 start 这个类来让我们选择的都是初始布局中的元素,来保证目标布局不变。然后,我们拿到选中的滑块的位置。位置是用 x,y 这种形式存的。然后我们拿到了行和列的值,存在 posRow 和 posCol 这两个变量中。
接下来的代码是用来执行移动的。
// Move Up
if (posRow + 1 == emptytilePosRow && posCol == emptytilePosCol) {
$(this).animate({
'top': "+=" + cellDisplacement //moves up
});
$('#empty').animate({
'top': "-=" + cellDisplacement //moves down
});
emptytilePosRow -= 1;
$(this).attr('data-pos', (posRow + 1) + "," + posCol);
}
// Move Down
if (posRow - 1 == emptytilePosRow && posCol == emptytilePosCol) {
$(this).animate({
'top': "-=" + cellDisplacement //moves down
});
$('#empty').animate({
'top': "+=" + cellDisplacement //moves up
});
emptytilePosRow += 1;
$(this).attr('data-pos', (posRow - 1) + "," + posCol);
}
// Move Left
if (posRow == emptytilePosRow && posCol + 1 == emptytilePosCol) {
$(this).animate({
'right': "-=" + cellDisplacement //moves right
});
$('#empty').animate({
'right': "+=" + cellDisplacement //moves left
});
emptytilePosCol -= 1;
$(this).attr('data-pos', posRow + "," + (posCol + 1));
}
// Move Right
if (posRow == emptytilePosRow && posCol - 1 == emptytilePosCol) {
$(this).animate({
'right': "+=" + cellDisplacement //moves left
});
$('#empty').animate({
'right': "-=" + cellDisplacement //moves right
});
emptytilePosCol += 1;
$(this).attr('data-pos', posRow + "," + (posCol - 1));
}
// Update empty position
$('#empty').attr('data-pos', emptytilePosRow + "," + emptytilePosCol);
每个 if 语句表示不同的移动方向。他们开起来差不多,只是条件,移动方向和更新的变量不同而已。比如向右移动,要看空的滑块是不是在当前移动的滑块的左边:posRow === emptytilePosRow 表示在一行,posCol - 1 === emptytileCol 表示空白的滑块在当前移动的滑块的左边一列。
如果条件满足,则执行 jquery 的动画,我们改变 right 属性的值,来移动当前选中的滑块。if 的条件语句的最后,我们修改 emptytilePosCol 的值,在其原来的值上加 1 ,因为空白的滑块向右移动了一格。同时我们修改当前移动的滑块的位置的值,列数减1。最后我们改变空白滑块的位置。
人工智能
A* 搜寻算法( Hart 等人在 1968 年提出)是用来计算多节点路径中两点之间最短距离的算法。我们用它来开发解答滑块游戏的功能。一个人工智能是能够在某种环境下按照特定的规则完成特定的任务的一种工具。最终的解法将有人工执行这个工具通过正确的决策来寻找。
人类在大部分情况下是理性的。一个人会根据所处环境的不同,从环境中得到信息,来对特定的情况采取理性的行为。比如在寒冷的冬天,我们会感到寒冷,于是我们会穿上厚厚的外套。
在滑块游戏这个场景下,环境是由整个板子决定的。滑块游戏的规则决定某个滑块能够向某个方向移动。如果该搜寻算法是有效的话,那么在一定的移动步数后,滑块的布局会变成目标布局。
A* 搜寻算法能做什么
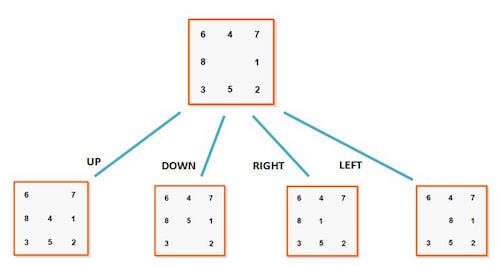
A* 搜寻算法能够找到从一种空间布局到另一种空间布局转换方法。搜寻是否智能是根据转换过程中操作的步数来判断的,步数越少,算法越智能。为了能方便描述布局状态,我们把问题转换成图形。我们认为状态 B 是状态 A 的下一种状态,也就是说要到状态 B 就要先到状态 A ,由状态 A 通过移动一个滑块就能够到达状态 B 了。所以一个状态节点会有如下的四中子状态节点。
A* 算法下节点示意图
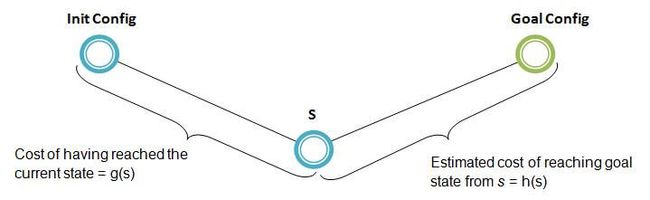
A* 搜寻算法基本思路是根据外界环境来选择下一步的行为。外界环境是由数字组成的。假设状态为 s ,那么
f(s) = g(s) + h(s)
其中 g(s) 是从初始状态到状态 s 的总步数,h(s) 是从状态 s 到目标状态的总步数,所以总步数是 f(s) 。
从其实状态到目标状态的总步数
我们使用启发式来寻找这巨大可能中的情况。启发式是一种载体,我们可以通过它将我们的经验和特定环境传递到人工智能算法中去,也就是传递到 A* 算法中去。通过启发式,我们就能找到解答问题的最短的途径了。
既然我们已经把问题转换成图像了,那么 A* 算法的大概框架就变得和 BFS 算法(广度优先算法)差不多了。BFS 算法是一种经典的图形节点算法。 A* 算法和 BFS 算法的区别在于, A* 算法中下一环节开始计算的节点的选择是和 f(s) 的值关联的,会优先选择最短的 f(s) 来优先计算 ,但是在 BFS 算法中,所有节点的选择权重都是 1 ,所以哪个路径更短并没有任何影响,在 BFS 算法中,下一环节的计算会从先记录的节点开始,也就是先进先出(FIFO)的队列原则。
我们建立启发式的时候,一定要保证其中包含了所有关键信息。不知道这段是什么意思。不过大概说了要有个条件让 A* 算法能找到最优解,类似于函数收敛则能找到极值。
前面说到我们要用 javascript 来写人工智能,有些人大概会认为这是不明智的,不过后面我会证明 javascript 拥有足够的能力。我们先写一个 Node 对象。
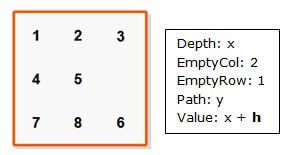
var Node = function (value, state, emptyRow, emptyCol, depth) {
this.value = value;
this.state = state;
this.emptyCol = emptyCol;
this.emptyRow = emptyRow;
this.depth = depth;
this.strRepresentation = '';
this.path = '';
// String representation of the state in CSV format
for (var i = 0; i < state.length; i++) {
// We assume the state is a square
if (state[i].length !== state.length) {
alert('Number of rows differs from number of columns');
return;
}
for (var j = 0; j < state[i].length; j++) {
this.strRepresentation += state[i][j] + ',';
}
}
this.size = this.state.length;
};
每个变量的说明如下:
valuef(s) 的值state用二维数组保存滑块排布的状态emptyCol记录空滑块所在的列emptyRow记录空滑块所在的行depth记录从起始状态到现在的步数strRepresentationCSV 字符串的形式保存滑块布局的状态。比如目标布局的值是 1,2,3,4,5,6,7,8 。滑块游戏布局是一个可以循环的游戏,也就是说从状态 s 经过一定的移动可以回到状态 s 。因此我们需要记录下每步的布局来避免走重复的路。这里我们会用 HashSet 。path记录每步的移动,用 DLRU 。这个字符串保存的是从其实布局到当前布局走过的路。size滑块游戏推盘的大小,我们假设推盘是 n 乘以 m 的,n 等于 m 。
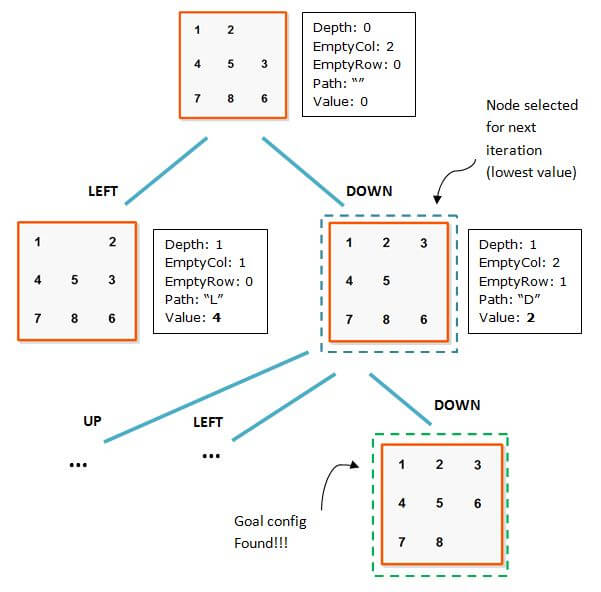
现在我们有了 Node 这个对象,我们来用个例子演示一下使用 A* 算法解题的过程。我们用最简单的启发式,根据放错位置的滑块的个数来。错位启发式返回的值就是不在自己应该在的位置的滑块的个数。这里说明了这个启发式是可接受的。
A* 搜寻算法
下面我们来实现 A* 算法:
var AStar = function (initial, goal, empty) {
this.initial = initial;
this.goal = goal;
this.empty = empty;
this.queue = new PriorityQueue({
comparator: function (a, b) {
if (a.value > b.value) {
return 1;
}
if (a.value < b.value) {
return -1;
}
return 0;
}
});
this.queue.queue(initial);
this.visited = new HashSet();
};
上面我们以及功能使用了之前定义的数据结构。优先队列中我们定义了一种排序方法,我们会把 f(s) 较小的状态放在前面。哈希对中存放 strRepresentation 记录所有到达过的状态,来避免重复。
现在我们用原型链给 A* 算法添加方法。 原型链 prototype 是一种方法或者属性,在创建新对象实例时,这个方法或者属性会成为新实例的一部分。比如, execute 这个方法会在所有 AStar 对象中存在。
AStar.prototype.execute = function () {
// Add current state to visited list
this.visited.add(this.initial.strRepresentation);
while (this.queue.length > 0) {
var current = this.queue.dequeue();
if (current.strRepresentation === this.goal.strRepresentation) {
return current;
}
this.expandNode(current);
}
};
execute 方法在以下几点上像 BFS :
有循环,循环结束于优先队列结束后。
当前的变量存放的是队列中的最小值。
如果节点的状态与目标状态匹配的话,那么我们认为整个搜寻任务结束。
如果搜寻任务没有结束,那么我们会对当前的节点进行展开。也就是在当点状态下执行每个方向的移动,然后把新的节点添加到队列中。
对节点展开的方法如下:
AStar.prototype.expandNode = function (node) {
var temp = '';
var newState = '';
var col = node.emptyCol;
var row = node.emptyRow;
var newNode = '';
// Up
if (row > 0) {
newState = node.state.clone();
temp = newState[row - 1][col];
newState[row - 1][col] = this.empty;
newState[row][col] = temp;
newNode = new Node(0, newState, row - 1, col, node.depth + 1);
if (!this.visited.contains(newNode.strRepresentation)) {
newNode.value = newNode.depth + this.heuristic(newNode);
newNode.path = node.path + 'U';
this.queue.queue(newNode);
this.visited.add(newNode.strRepresentation);
}
}
// Down
if (row < node.size - 1) {
newState = node.state.clone();
temp = newState[row + 1][col];
newState[row + 1][col] = this.empty;
newState[row][col] = temp;
newNode = new Node(0, newState, row + 1, col, node.depth + 1);
if (!this.visited.contains(newNode.strRepresentation)) {
newNode.value = newNode.depth + this.heuristic(newNode);
newNode.path = node.path + 'D';
this.queue.queue(newNode);
this.visited.add(newNode.strRepresentation);
}
}
// Left
if (col > 0) {
newState = node.state.clone();
temp = newState[row][col - 1];
newState[row][col - 1] = this.empty;
newState[row][col] = temp;
newNode = new Node(0, newState, row, col - 1, node.depth + 1);
if (!this.visited.contains(newNode.strRepresentation)) {
newNode.value = newNode.depth + this.heuristic(newNode);
newNode.path = node.path + 'L';
this.queue.queue(newNode);
this.visited.add(newNode.strRepresentation);
}
}
// Right
if (col < node.size - 1) {
newState = node.state.clone();
temp = newState[row][col + 1];
newState[row][col + 1] = this.empty;
newState[row][col] = temp;
newNode = new Node(0, newState, row, col + 1, node.depth + 1);
if (!this.visited.contains(newNode.strRepresentation)) {
newNode.value = newNode.depth + this.heuristic(newNode);
newNode.path = node.path + 'R';
this.queue.queue(newNode);
this.visited.add(newNode.strRepresentation);
}
}
};
这里的 if 条件语句都很像,差别只是他们针对的移动方向不同。首先,我们判断一下这步是否能够正常进行。比如向右移动,只有空滑块的列数小于推盘的行数才行。如果这步能够正常移动,那么我们建立一个新的状态 newState ,这个状态是从当前状态复制出来的。然后我们交换空白滑块和对应元素,同时修改 newState ,最后我们判断一下这个状态是不是已经存在了,如果没有存在的话,把这个状态记录到队列中去。我们还要计算一下节点的值,按照之间提到过的 f = g + h ,然后在 path 变量中记录下移动的方向。
Array.prototype.clone = function () {
return JSON.parse(JSON.stringify(this));
};
最后别忘了启发式方法
AStar.prototype.heuristic = function (node) {
return this.manhattanDistance(node);
};
这里开始,我们就能比较不用启发式下的 A* 算法的效率了。我们会慢慢发现一个启发式对于算法来说是至关重要的,其智能程度极大地影响了算法的耗时。
错位滑块
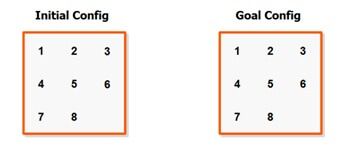
在我们进入有趣的启发式之前,先记得在计算启发式的时候,我们绝对不会考虑空白滑块。否则我们就会过高估路径的步数了,那么启发式可能不能被接受了。比如下面这个情况:
如果们我考虑空白滑块,那么 h 就是 2 了,而事实上,我们只要把空白滑块向下移动一步就行了。因此实际的最短步数是 1 ,而不是二,我们高估路径的步数了。
为了测试我们的启发式,我们用一个最差情况来试一试,这个情况下需要 31 步才能完成解答。
A* 算法在点击 Solve 按钮后会执行。onclick 触发的事件是执行 start 方法,方法的内容如下:
var start = function () {
var init = new Node(0, [[6, 4, 7], [8, 5, 0], [3, 2, 1]], 1, 2, 0);
var goal = new Node(0, [[1, 2, 3], [4, 5, 6], [7, 8, 0]], 2, 2, 0);
var aStar = new AStar(init, goal, 0);
// To measure time taken by the algorithm
var startTime = new Date();
// Execute AStar
var result = aStar.execute();
// To measure time taken by the algorithm
var endTime = new Date();
alert('Completed in: ' + (endTime - startTime) + ' milliseconds');
var panel = document.getElementById('panel');
panel.innerHTML = 'Solution: ' + result.path + ' Total steps: ' + result.path.length + '';
solution = result.path;
};
我们用毫秒来记录算法的耗时。用这种方式来评估不同启发式之间的优劣。错位滑块启发式的代码如下:
AStar.prototype.misplacedTiles = function (node) {
var result = 0;
for (var i = 0; i < node.state.length; i++) {
for (var j = 0; j < node.state[i].length; j++) {
if (node.state[i][j] != this.goal.state[i][j] && node.state[i][j] != this.empty) {
result++;
}
}
}
return result;
};
执行结果如下:
算法花了将近 4 秒来解答,诶哟,不错哟。但是我们可以用一个更加棒的启发式来让计算更快。
曼哈顿距离
曼哈顿距离或者块距离是用来计算两点间距离的绝对值的。
MD = | x1 - x2 | + | y1 - y2 |
A 点 (x1, y1) 和 B 点 (x2, y2) 之间的距离
这个结果是可接受的,因为它永远给出的是两点之间最短的路径。
AStar.prototype.manhattanDistance = function (node) {
var result = 0;
for (var i = 0; i < node.state.length; i++) {
for (var j = 0; j < node.state[i].length; j++) {
var elem = node.state[i][j];
var found = false;
for (var h = 0; h < this.goal.state.length; h++) {
for (var k = 0; k < this.goal.state[h].length; k++) {
if (this.goal.state[h][k] == elem) {
result += Math.abs(h - i) + Math.abs(j - k);
found = true;
break;
}
}
if (found) {
break;
}
}
}
}
return result;
};
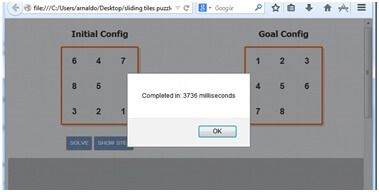
使用了这个启发式的结果如下:
我们已经大大减少了计算时间,现在只要 1 秒不到。曼哈顿距离这个启发式更加精确地估算了离目标布局的步数,因此我们可以更快地到达目的地。
结合曼哈顿距离和线性冲突
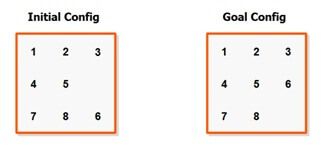
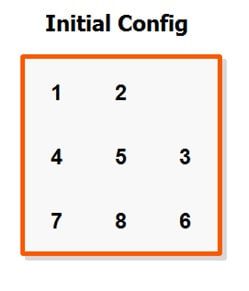
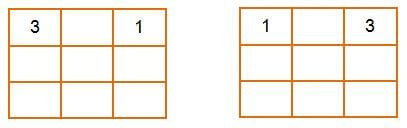
尽管吗哈顿距离大大缩小了算法的耗时,但是依然有很多优化可以做。线性冲突启发式提供了这个关键点。如果 tj 和 tk 这两个是在用一条线上,并且他们两个的目的地都是在这条线上,并且 tj 要去 tk 那个方向,tk 要去 tj 那个方向,那么我们说 tj 和 tk 是线性冲突的。
左边的布局,滑块 3 和滑块 1 在一行中,但是不在正确的位置。为了让他们能够到正确的位置上去,我们必须把其中一块向下移动,再把它移上来,这个移动的行为在曼哈顿距离启发式中没有考虑进去。要注意,一个滑块不可能和很多个滑块产生线性冲突,因为解决了一个线性冲突后,也就解决了这一行的所有线性冲突了。因此,如果滑块 1 和滑块 3 是线性冲突的,那么滑块 1 和滑块 2 就不是线性冲突的了,否则启发式就变得不可接受,我们会高估解答的步数。线性冲突启发式的代码如下:
AStar.prototype.linearConflicts = function (node) {
var result = 0;
var state = node.state;
// Row Conflicts
for (var i = 0; i < state.length; i++) {
result += this.findConflicts(state, i, 1)
}
// Column Conflicts
for (var i = 0; i < state[0].length; i++) {
result += this.findConflicts(state, i, 0)
}
return result;
};
AStar.prototype.findConflicts = function (state, i, dimension) {
var result = 0;
var tilesRelated = [];
// Loop foreach pair of elements in the row/column
for (var h = 0; h < state.length - 1 && tilesRelated.indexOf(h) === -1; h++) {
for (var k = h + 1; k < state.length && tilesRelated.indexOf(h) === -1; k++) {
var moves = dimension == 1
? this.inConflict(i, state[i][h], state[i][k], h, k, dimension)
: this.inConflict(i, state[h][i], state[k][i], h, k, dimension);
if (moves == 0) {
continue;
}
result += 2;
tilesRelated.push([h, k]);
break;
}
}
return result;
};
AStar.prototype.inConflict = function (index, a, b, indexA, indexB, dimension) {
var indexGoalA = -1;
var indexGoalB = -1;
for (var c = 0; c < this.goal.state.length; c++) {
if (dimension == 1 && this.goal.state[index][c] == a) {
indexGoalA = c;
} else if (dimension == 1 && this.goal.state[index][c] == b) {
indexGoalB = c;
} else if (dimension == 0 && this.goal.state[c][index] == a) {
indexGoalA = c;
} else if (dimension == 0 && this.goal.state[c][index] == b) {
indexGoalB = c;
}
}
return (indexGoalA >= 0 && indexGoalB >= 0) &&
((indexA < indexB && indexGoalA > indexGoalB) ||
(indexA > indexB && indexGoalA < indexGoalB))
? 2
: 0;
};
既然线性冲突启发式和曼哈顿距离启发式之间不会发生冲突,那么我们可以把他们两个结合起来,来获得一个更加棒的算法。
AStar.prototype.heuristic = function (node) {
return this.manhattanDistance(node) + this.linearConflicts(node);
};
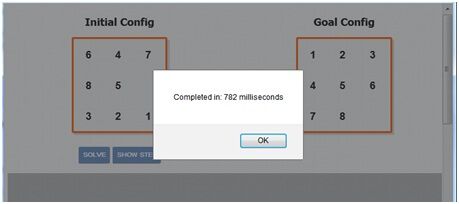
加入了线性冲突启发式后,结果如下:
加入了线性冲突启发式后,我们在计算速度上又提高了很大一截。如果想看结果的话,我们可以看灰色的面板上显示的内容。
按了 Show Step 按钮之后,我们可以看到解法的一步。按了 31 步之后,我们就能看到解答的整个过程了。
这篇文章我们介绍了用人工智能 A* 算法解推盘游戏的方法。我们验证了不同启发式下结果的正确性,并且成功地找到了一种非常有效的启发式。现在你可以用它来打败你的朋友们了。我们体会了人工智能的神奇,我们用它来解决了生活中的问题。人工智能的最终的目的是给我们带来更加轻松而高效的生活。