定义
关键路径是指设计中从输入到输出经过的延时最长的逻辑路径(从起点到终点的最长路径)。
最简单的求解办法
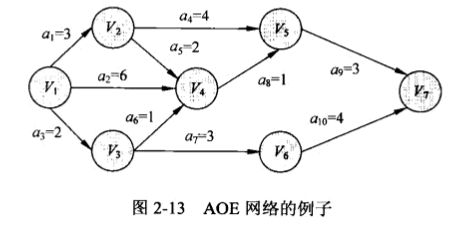
有了这个概念就可以求解大部分常见问题啦,比如下面这个AOE网,求一下关键路径和关键路径长度
不就是最长的路径嘛?像这种题如果是选择、填空或者简答题,最简单的办法就是列出所有路径长度,找出最长的,就是答案了。此题有2个关键路径,即V1-V2-V5-V7和V1-V4-V5-V7,长度都是10,答案就出来了。大概用时不到半分钟,如果按步骤用正常方法,估计至少需要几分钟的时间。
常规求解办法
但是遇到求解下面一些概念的时候,则不得不按常规方法做了:
(1) 事件开始的最早时间ve(i);
(2) 事件开始的最晚时间vl(i);
(3) 活动开始的最早时间e(i);
(4) 活动开始的最晚时间l(i) ;
定义e(i)=l(i)的活动叫关键活动,也就是关键路径上的活动;
下面还是以上图为例,求解上面4个时间(注意AOE网中顶点代表事件,边代表活动):
求解顺序是,先求ve(i),然后是vl(i),再然后根据这两个即可分别求得vl(i)、l(i)。
还是这个图:
ve(i):
从起点开始向终点找
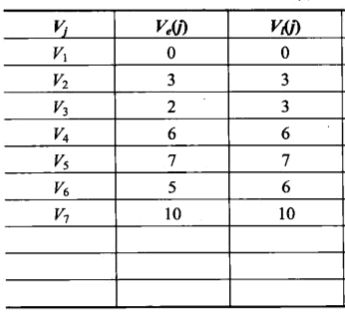
先看V1,作为第一个事件,V1的最早开始时间ve(i)毫无疑问应该是0;
然后是V2,从V1到它只有一条路径(a1=3),那么它的最早开始时间应该是0+3=3;
同理V3,应该就是0+2=2;
重点是V4,从V1到它有3条路径,分别是(a1=3,a5=2)、(a2=6)、(a3=2,a6=1),其中第二个路径最长为6,第3个最短为3。由最早开始,容易想到路径最短,但是要注意AOE网下面的性质(2):
(1)只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始。
(2)只有在进入某点的各有向边所代表的活动都已结束,该顶点所代表的时事件才能发生。
只有a2完成后,才能算都结束,所以V4的最早开始时间ve(i)是6;
小结:Vi的最早开始时间ve(i)就是从起点到它的最长路径;
vl(i):
从终点开始向起点找
先看V7,算V7的ve(i)时就已经得出,从起点到它最多需要10,所以它的最晚开始时间vl(i)也不能再多于10 了,也即vl(i)=ve(i)=10。
然后是V6,V7最晚开始是10,而V6到V7需要4,所以V6再晚也不能晚于10-4=6吧;
同理V5,是10-3=7,V4,是7-1=6;
重点是V2,有V4和V5两个事件限制它,V5需要它最晚不能晚于7-4=3,V4需要它不能晚于6-2=4,
所以它最晚不能晚于3不难理解吧?
小结:从终点倒推,终点的vl(i)=ve(i),事件i的直接后续事件减去活动时间为要求它最晚开始的事件,其中最小的一个就是它的vl(i);
所有事件的ve(i)和vl(i):
有了ve(i)和vl(i),e(i)和l(i)就好求了:
e(i):
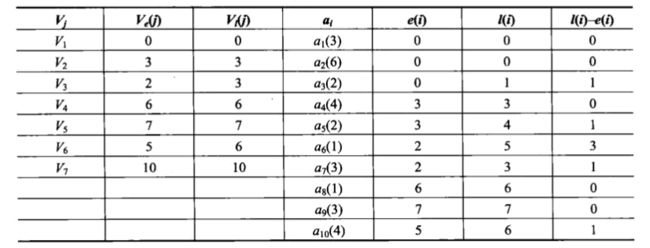
ai的e(i)就等于ai的起点(弧头)事件的ve(i),比如a1、a2、a3的e(i)等于V1的ve(i)都是0,a4的e(i)是3;
l(i):
ai的l(i)就等于ai的终点(弧尾)事件的vl(i)减去ai,比如a7的l(i)是V7的vl(i)减去ai,即10-4=6,a5、a2、a6的l(i)分布是6-2=4、6-6=0、6-1=5
最终结果:
其中e(i)=l(i)即e(i)-l(i)=0的活动,就是关键活动啦。
其他需要注意概念与性质
(1) 求关键路径必须在拓扑排序的前提下进行,有环图不能求关键路径;
(2) 只有缩短关键活动的工期才有可能缩短工期;
(3) 若一个关键活动不在所有的关键路径上,减少它并不能减少工期;
(4) 只有在不改变关键路径的前提下,缩短关键活动才能缩短整个工期。
注意这个“有可能”,还是以上题为例,如果把关键活动a4由4缩短为3,并不能缩短关键路径的长度,它还是10,因为这样V1-V4-V5-V7的最长度为9,已经不是关键路径了;
那么把公共的关键活动a9由3缩短为2呢?这样是可以的,关键路径长度变为9;
把a9由3缩短为1呢?那V1-V2-V5-V7和V1-V4-V5-V7就都不是关键路径了;
习题
试试下面两个题?
按简单方法,是不是几秒钟就可以选出正确答案?
.
.
.
.
.
.
.
.
.
.
.
.
.
正确答案:A
从上至下第一条路径的长度就是20,而选项里最大就是20。
能有效缩短关键路径长度的方法是()。
A.缩短任意一个活动的持续时间
B.缩短关键路径上任意一个关键活动的持续时间
C.缩短多条关键路径上共有的任意一个关键活动的持续时间
D.缩短所有关键路径上共有的任意一个关键活动的持续时间
.
.
.
.
.
.
.
.
.
.
.
.
.
.
正确答案:D
关键路径是始点和终点间的最长路径,只有所有关键路径的长度都缩短,整个图的关键路径才能有效缩短,但也不能任意缩短,一旦缩短到一定程度,该关键活动可能变成非关键活动了。