308. Range Sum Query 2D - Mutable

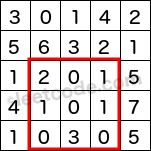
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Range Sum Query 2D

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

Given matrix = [
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10

Note:

1. The matrix is only modifiable by the update function.
2. You may assume the number of calls to update and sumRegion function is distributed evenly.
3. You may assume that row1 ≤ row2 and col1 ≤ col2.

一刷
题解： 二维Binary Indexed Tree

public class NumMatrix {

    int[][] tree;
    int[][] nums;
    int m;
    int n;
    
    public NumMatrix(int[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) return;
        m = matrix.length;
        n = matrix[0].length;
        tree = new int[m+1][n+1];
        nums = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                update(i, j, matrix[i][j]);
            }
        }
    }

    public void update(int row, int col, int val) {
        if (m == 0 || n == 0) return;
        int delta = val - nums[row][col];
        nums[row][col] = val;
        for (int i = row + 1; i <= m; i += i & (-i)) {
            for (int j = col + 1; j <= n; j += j & (-j)) {
                tree[i][j] += delta;
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        if (m == 0 || n == 0) return 0;
        return sum(row2+1, col2+1) + sum(row1, col1) - sum(row1, col2+1) - sum(row2+1, col1);
    }
    
    public int sum(int row, int col) {
        int sum = 0;
        for (int i = row; i > 0; i -= i & (-i)) {
            for (int j = col; j > 0; j -= j & (-j)) {
                sum += tree[i][j];
            }
        }
        return sum;
    }
}
// time should be O(log(m) * log(n))

二刷
同上 segment tree

public class NumMatrix {
    
    class TreeNode {
        int row1, row2, col1, col2, sum;
        TreeNode c1, c2, c3, c4;
        public TreeNode (int row1, int col1, int row2, int col2) {
            this.row1 = row1;
            this.col1 = col1;
            this.row2 = row2;
            this.col2 = col2;
            this.sum = 0;
        }
    }

    TreeNode myroot;
    
    public NumMatrix(int[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) return;
        
        myroot = buildTree(matrix, 0, 0, matrix.length-1, matrix[0].length-1);    
    }
    
    private TreeNode buildTree(int[][] matrix, int row1, int col1, int row2, int col2) {
        if (row2 < row1 || col2 < col1) return null;
            
        TreeNode node = new TreeNode(row1, col1, row2, col2);
        if (row1 == row2 && col1 == col2) {
            node.sum = matrix[row1][col1];
            return node;
        }
        
        int rowMid = row1 + (row2 - row1) / 2;
        int colMid = col1 + (col2 - col1) / 2;
        node.c1 = buildTree(matrix, row1, col1, rowMid, colMid);
        node.c2 = buildTree(matrix, row1, colMid+1, rowMid, col2);
        node.c3 = buildTree(matrix, rowMid+1, col1, row2, colMid);
        node.c4 = buildTree(matrix, rowMid+1, colMid+1, row2, col2);
        
        node.sum += (node.c1 == null) ? 0 : node.c1.sum;
        node.sum += (node.c2 == null) ? 0 : node.c2.sum;
        node.sum += (node.c3 == null) ? 0 : node.c3.sum;
        node.sum += (node.c4 == null) ? 0 : node.c4.sum;
        return node;
    }

    public void update(int row, int col, int val) {
        updateTree(myroot, row, col, val);
    }
    
    private void updateTree(TreeNode root, int row, int col, int val) {
        if (root == null) return;
        
        if (row < root.row1 || row > root.row2 || col < root.col1 || col > root.col2)
            return;
            
        if (root.row1 == root.row2 && root.row1 == row && root.col1 == root.col2 && root.col1 == col) {
            root.sum = val;
            return;
        }
            
        updateTree(root.c1, row, col, val);
        updateTree(root.c2, row, col, val);
        updateTree(root.c3, row, col, val);
        updateTree(root.c4, row, col, val);
        
        root.sum = 0;
        root.sum += (root.c1 == null) ? 0 : root.c1.sum;
        root.sum += (root.c2 == null) ? 0 : root.c2.sum;
        root.sum += (root.c3 == null) ? 0 : root.c3.sum;
        root.sum += (root.c4 == null) ? 0 : root.c4.sum;
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sumRegionTree(myroot, row1, col1, row2, col2);
    }
    
    private int sumRegionTree(TreeNode root, int row1, int col1, int row2, int col2) {
        if (root == null) return 0;
        
        if (root.row2 < row1 || root.row1 > row2 || root.col2 < col1 || root.col1 > col2)
            return 0;
        
        if (root.row1 >= row1 && root.row2 <= row2 && root.col1 >= col1 && root.col2 <= col2)
            return root.sum;
        
        return sumRegionTree(root.c1, row1, col1, row2, col2) + 
               sumRegionTree(root.c2, row1, col1, row2, col2) +
               sumRegionTree(root.c3, row1, col1, row2, col2) +
               sumRegionTree(root.c4, row1, col1, row2, col2);
    }
}