第一二天图形

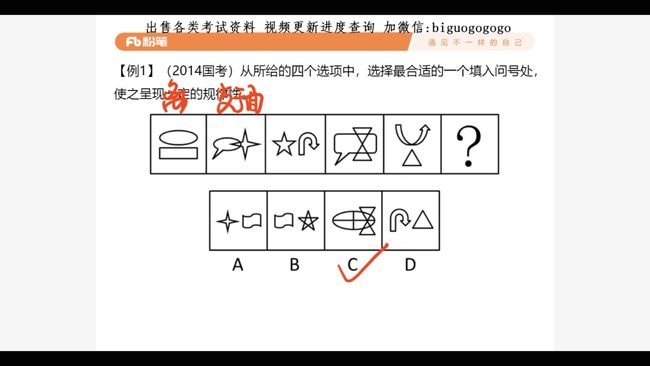
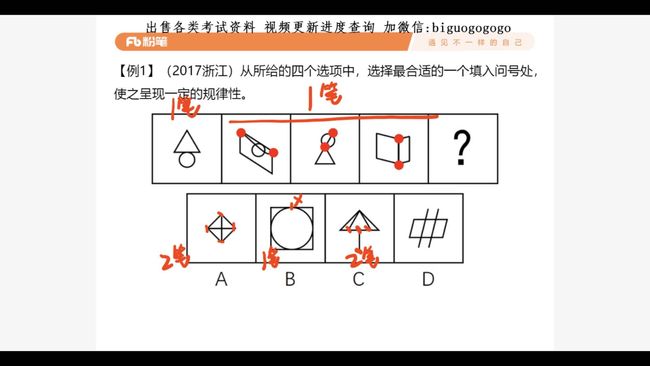
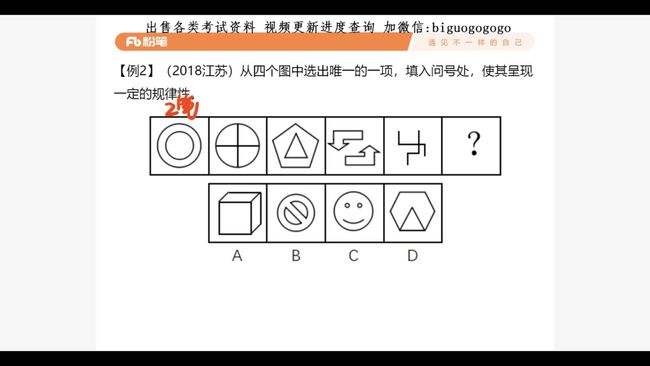
1. 图形推理命题形式(3.47)

• 一组图 (常见)
• 两组图 (常见)
• 九宫格 (常见)
• 分组分类
• 空间类(折纸盒)

2. 图形推理规律(5.56)

• 位置规律(元素组成相同)

1. 平移 2. 旋转/翻转

• 样式规律(元素组成相似)

1. 遍历 2. 加减异同 3. 黑白运算

• 属性规律(元素组成不同)

1. 对称性 2. 曲直性 3. 开闭性

• 特殊规律(不相同, 不相似, 无属性规律)

1. 图形间关系(相交点, 边, 面) 2. 功能元素(相同小元素(点, 箭头等)标记)

• 数量规律(不相同, 不相似, 无属性规律, 无特殊规律)

1. 面 2. 线 3. 点 4. 素

• 空间规律

3. 位置规律(7.11)

• 题型识别: 图形元素组成相同
• 方法:

1. 方向: 直线, 绕圈(顺时针/逆时针)
2. 步数: 恒定, 等差递增
3. 位置规律 - 就近原则很重要
4. 边做边排除

3.1 平移案例

11575512605_.pic.jpg

4. 黑块平移问题(27.07)

解题原则:

• 黑块如何辨析: 就近假设(重要)
  对黑块1而言, a的位置近, 所以1移动到a;
  同理, 黑块2移动到b
  
  

  image.png
• 位移到头:

1. 循环走: 从头开始(为主) - 1234 1234 ...
2. 反弹走: 弹回 - 1234 321 ...

• 黑块可重合:
  题干和选项大部分元素组成完全一致, 个别一两副图缺少黑块, 表示有黑块重合
  题干第一幅图黑块数量一般最多, 不会重合

4.1 黑块平移, 案例

31575515949_.pic.jpg

5. 区分旋转&翻转(41.25)

71573114203_.pic.jpg

5.1 旋转案例

注意: 结合选项差异, 快速解题

41575516607_.pic.jpg

5.2 旋转, 案例

51575517149_.pic.jpg

5.3 旋转, 总结

识别与方法:

1. 有中心点, 从中心点向外发射线
2. 线的辨析, 判断旋转方向 - 就近原则
3. 看夹角, 判断旋转角度

案例:

61575518048_.pic.jpg

6. 样式, 相似遍历---缺啥补啥(48.50)

81573115172_.pic.jpg

6.1 遍历, 案例

71575525282_.pic.jpg

6.2 遍历小结

1. 数量遍历
2. 颜色遍历
3. 位置遍历

81575525736_.pic.jpg

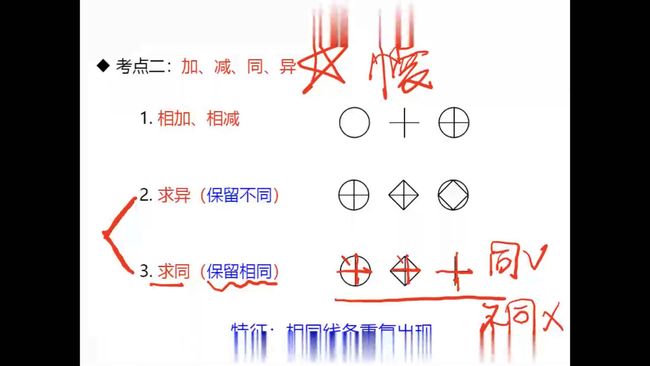
7. 样式, 加减同异(57.09)

特征: 元素相似, 相同线条重复出现

91573117820_.pic.jpg

7.1 样式, 加减异同, 案例

快速加减异同解法: 结合选项挑1-2条线进行比较,
4个选项都存在差异, 挑1条线就能找到答案
两两选项存在差异, 挑2条线可以确定答案

91575526280_.pic.jpg

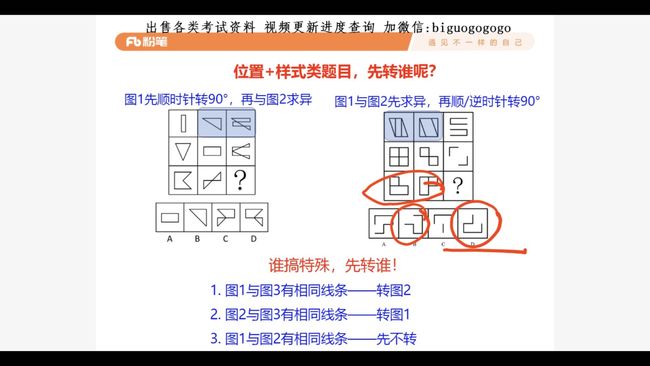
7.2 样式, 加减异同, 小结

问题: 带有旋转的加减异同, 先转谁?
技巧: 谁特殊, 先转谁?

101575527552_.pic.jpg

9. 样式, 黑白运算***(1.17.06)

黑 + 黑 = 黑
白 + 白 = 黑
黑 + 白 = 白
白 + 黑 = 黑

9.1 黑白运算和位置关系的区别(1.17.25)

• 黑块数量相同: 优先位置平移
• 黑块数量不同: 优先黑白运算

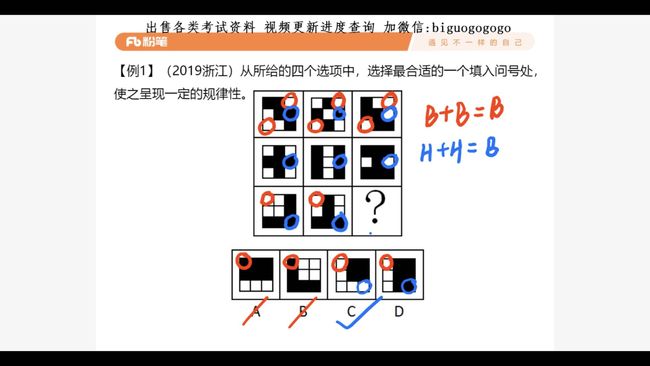
9.2 黑白运算, 案例

分析:

1. 根据黑块数量不同, 确定是黑白运算
2. 观察选项, 选项可分为两组, 通过右上角"白+ 白 = 白", 排除AB
3. 通过右下角"黑 + 黑 = 白", 确定C

技巧: 根据选项差异, 去题干验证

111575529479_.pic.jpg

11. 属性规律(1.35.48)

识别: 元素组成不相同, 不相似
考点:

1. 对称性***(重点)
2. 曲直性
3. 开闭性

12. 对称性特点***(1.39.49)

特点: 规整, 出现等腰元素, 对称特性***

1. 轴对称 --- "等腰"元素
2. 中心对称 --- 平行四边形, N, Z, S
3. 两者皆是 --- 存在相互垂直的对称轴

12.1. 对称性的细化(1.45.0)

1. 先看对称性, 轴对称还是中心对称还是皆是
2. 对称轴的数量和方向
3. 对称轴与图形中的线的位置关系(重合, 垂直, 平行)
4. 对称轴与图形的交点数量, 经过面的数量(比较难)

12.2 对称,数量 案例

分析:

1. 根据规整, 等腰元素, 判断考对称特性
2. 画出每个图形的对称轴(重要)***
3. 发现 对称轴个数1,2,3 递增特性, 选D
   
   

   121575531279_.pic.jpg

12.3 对称,位置关系 案例

分析:

1. 根据规整, 等腰元素, 判断考对称特性
2. 画出每个图形的对称轴(重要)***
3. 发现 对称轴 与图形中的一条线重合, 选D
   
   

   141575531724_.pic.jpg

12.4 对称, 位置关系, 经过面, 案例

分析:

1. 根据规整, 等腰元素, 判断考对称特性
2. 画出每个图形的对称轴(重要)***
3. 发现, 234对称轴经过一个面, 156对称轴经过3个面, 选D

161575533047_.pic.jpg

12.5 对称轴, 小结

1. 识别题型, 有规整, 等腰元素, 判断考对称特性
2. 快速做出判断, 轴对称还是中心对称, 还是两者都有
3. 画出所有对称轴, 以备便于观察
4. 观察 对称轴 数量, 方向
5. 观察 对称轴与图形中线/面的位置关系
6. 观察 对称轴之间的位置关系

171575533769_.pic.jpg

14.属性规律, 曲直性(1.55.0)

考点:

1. 全直线图
2. 全曲线图
3. 曲线+直线

14.1 曲直性, 案例

分析:

1. 题干中图形 元素组成不相同
2. 存在不规整, 不对称图形
3. 考虑 曲直特性, 发现 135全曲, 246全直, 选B

181575534317_.pic.jpg

15. 开闭性案例(2.0.9)

题型识别:

1. 元素组成不同
2. 存在非对称图形
3. 完整图形开了小口

类型:

1. 全封闭
2. 开放
3. 半封闭 (如 字母A)

15.1 开闭性, 案例

分析:

1. 存在 非对称图形, 曲直线条不明显
2. 图26中存在, 完整图形有小口, 可以考虑开闭性`
3. 观察 236开放图形, 145全封闭图形, 选B

191575536041_.pic.jpg

15.2 开闭性, 案例

分析:

1. 考虑 元素组成不同, 无对称特性, 无曲直特性
2. 观察到第5个图有一个小开口, 考虑开闭性
3. 题干所给的所有图形都是开放图形, 选项只有一个开放图形, 其余都是半封闭图形, 选A

201575536537_.pic.jpg

16. 特殊规律

1. 图形间关系(相交/相离)
2. 功能元素

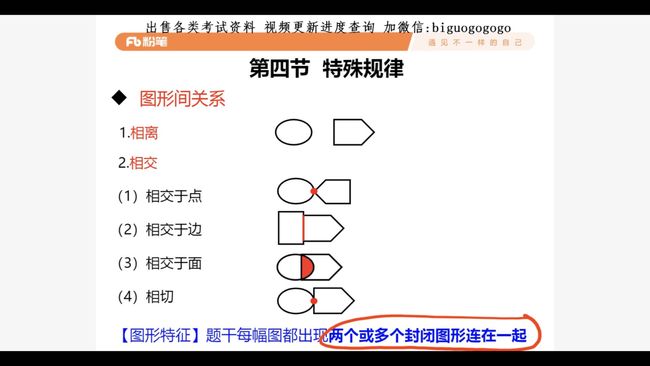
16.1 特殊规律, 图形间关系(2.18.18)

考点:

1. 相离
2. 相交
   2.1 相交于点
   2.2 相交于边
   2.3 相交于面
   2.4 相切

识别:

1. 元素组成不相同, 无明显属性规律(对称, 曲直, 开闭)
2. 题干每幅图出现两个或多个封闭图形连在一起
3. 每幅图 之间用线相连认为相交于点

211575537638_.pic.jpg

16.2 图形间关系, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 发现 有图形 两两相离, 有两两相交, 考虑图形间关系
3. 发现 图形间交替相离相交规律, 推出问号应该是相交特性, 选项只有C符合

221575537832_.pic.jpg

16.3 图形间关系, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 观察 每幅图形之间 都是用线相连, 认为相交于点
3. 只有C 图形相交于点

231575538425_.pic.jpg

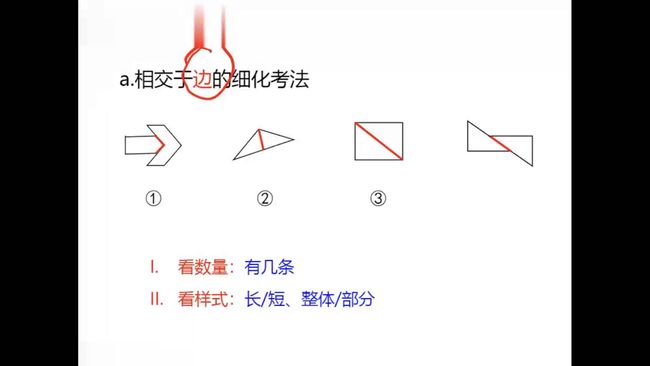
16.4 特殊规律, 图形关系, 相交于边的细化

方法:

1. 观察发现, 都是相交于边的
2. 把所有的边画出来, 以备比较

细化考法:

1. 数量
2. 长短
3. 整体部分

31573132378_.pic.jpg

16.5 图形间关系, 细化案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 观察图形都是相交于边, 考虑图形间关系
3. 发现 356都是部分相交, 选B

241575539190_.pic.jpg

16.6 图形间关系, 细化案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 观察图形都是相交于边, 考虑图形间关系
3. 发现 146 相交于短边, 选A

251575539421_.pic.jpg

16.7 特殊规律, 图形关系, 相交于面的细化

方法:

1. 观察发现, 都是相交于面的
2. 把所有的面画出来, 以备比较

细化考法:

1. 相交面的形状
2. 两个或多个面分别的形状 与 相交面的形状(相似, 相同)

11575553702_.pic.jpg

16.8 图形关系, 相交面细化, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 观察图形都是相交于面, 考虑图形间关系相交于面
3. 画出相交面, 发现相交面 边数量 3, 4, 5, 6...递增, 所以选C

21575554022_.pic.jpg

16.9 图形关系, 相交面细化, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 观察图形都是相交于面, 考虑图形间关系相交于面
3. 画出相交面, 发现相交面与其他图形相似, 所以选D

31575554266_.pic.jpg

17. 特殊规律, 功能元素(必考)***

识别: 均有相同小元素(点, 箭头等)标记, 优先考虑功能元素

17.1 功能元素, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 每幅图都有小元素标记
3. 发现124, 标记位于相交面外, 356位于相交面内, 所以选C

41575554996_.pic.jpg

17.2 功能元素, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 每幅图都有小元素标记
3. 发现134标记位于左侧, 256位于右侧, 所以选D

61575555291_.pic.jpg

17.3 功能元素, 案例

分析:

1. 图形元素不相同/相似, 无明显属性规律(对称, 曲直, 开闭)
2. 每幅图都有小元素标记
3. 发现134标记位于最长边一侧, 256位于最短边一侧, 所以选A

51575555271_.pic.jpg

18. 数量规律

识别:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 考虑数量规律(需要数数, 费时间)

考点:

1. 面 2. 线 3. 点 4. 素

18.1 数面

识别:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 图形被分割, 封闭面明显
4. 生活化图形, 粗线条留白

细化(所有面数量无规律):

1. 重点观察面的形状
2. 所有面的形状(相同, 相似)
3. 相同形状的面的个数
4. 最大/最小面的特征

18.1.1 数面, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 发现图形都是封闭面组成, 考虑数量规律-数面
4. 得出面数量依次为2, 3, 4, 5, 6, ? , 选项C符合规律

11575616097_.pic.jpg

18.1.2 数面, 细化(所有面特征), 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 发现图形都是封闭面组成, 考虑数量规律-数面
4. 发现都是4个, 选项ACD符合
5. 细化规律, 题干的封闭面形状都是三角形, 只有D符合

21575618124_.pic.jpg

18.1.3 数面, 细化(最大面特征), 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 发现图形都是封闭面组成, 考虑数量规律-数面
4. 发现数量依次为3 4 5 6 7 ?
5. 同时, 细化规律, 发现 最大面的形状都是三角形, 答案选B

31575618416_.pic.jpg

18.1.4 数面, 细化(最大面特征), 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 发现图形都是封闭面组成, 考虑数量规律-数面
4. 发现都是5个面, 只能排除C, 考虑细化
5. 画出最大面, 发现最大面特征规整, 都是中心对称, 只有A符合

41575619145_.pic.jpg

18.1.5 数面, 细化(相同形状面数量), 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 发现图形都是封闭面组成, 考虑数量规律-数面
4. 发现所有面数量无规律, 考虑细化
5. 观察, 相同面数量规律依次 2 3 4 5 6 ? , 只有B符合

51575619730_.pic.jpg

18.2 数线

识别:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 数直线: 多边形, 单一直线
4. 数曲线: 曲线图形, 单一曲线, 圆, 弧

18.2.1 数线, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 都有曲线图形, 也有单一曲线, 考虑数曲线
4. 125 有3条曲线, 346有1条曲线, 选B

61575620571_.pic.jpg

18.2.2 数线, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 都有多边形, 也有单一值线, 考虑数直线
4. 题干都是11条直线, 只有C符合

71575621054_.pic.jpg

18.2.3 数线, 细化(内外分开数找规律), 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 都有多边形, 也有单一直线, 考虑数直线
4. 图形都是内外分开, 分开数得出 6/5, 5/4, 4/3, 4/3, 5/4
5. 发现内外直线数量差都是1, 只有A符合

81575621628_.pic.jpg

18.3 数量, 笔画***

判断一笔画:

1. 线条之间连通
2. 奇点数量0或2
   (奇点: 以一个点为中心, 发射出奇数条线)
   注意: 数奇点不要忘记数端点

多笔画:
(奇点数一定是偶数个)

识别:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 出现明显端点
4. 日, 田及其变形

11575703596_.pic.jpg

18.3.1 数量, 笔画, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 出现 日 田 变形图, 端点, 考虑笔画, 选B

21575704168_.pic.jpg

18.3.2 数量, 笔画, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 出现 日 田 变形图, 端点, 考虑笔画, 选A

31575704336_.pic.jpg

18.3.3 数量, 笔画, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 出现 日 田 变形图, 端点, 考虑笔画, 124是2笔画,356是1笔画 选B

41575704583_.pic.jpg

18.3.3 数量, 笔画, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 出现 日 田 变形图, 端点, 考虑笔画,都是2笔画, 选A

51575704752_.pic.jpg

18.4 数量, 数点**

识别:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 无数笔画特征
4. 线条交叉明显(大树叉)
5. 切点较多
6. 封闭图形与直线相交较多

细化:

1. 切点数量
2. 曲直交点
3. 内外交点

18.4.1 数点, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 无数笔画特征
4. 线条交叉明显(大树叉), 数点,依次1 2 3 4 5.. 选 B

61575705531_.pic.jpg

18.4.2 数点, 细化, 切点, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 无数笔画规律
4. 切点交多, 考虑数切点
5. 124是1个切点, 356是2个切点, 选B

71575706097_.pic.jpg

18.4.3 数点, 细化, 曲直交点, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 无数笔画规律
4. 题干图4曲直相交, 考虑曲直交点数
5. 曲直交点数, 依次234, 选C

81575706566_.pic.jpg

18.4.4 数点, 细化, 交点位置, 案例

分析:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 无数笔画规律
4. 观察图形都有圆形与直线相交, 考虑, 内外交点
5. 规律内部交点第一行1个, 第二行2个, 第三行3个, 选C

91575707382_.pic.jpg

19. 素数量

一种图形: 颜色, 形状一样认为是一种

考点:

1. 元素个数
2. 元素种类

细化:

1. 同种种类数量
2. 部分数 (出现生活化粗线条的)

识别:

1. 不相同, 不相似, 无属性规律(对称, 曲直, 开闭)
2. 无特殊规律(图形间关系, 功能元素)
3. 多个独立小图形

19.1 素数量, 个数和种类 案例

分析:

1. 多个独立小图形, 看素数量
2. 发现第1组数量规律765, 第2组65?, 应该是4, 排除BD
3. 发现第1组种类规律234, 第2组12?, 应该是3, 选C

101575708254_.pic.jpg

19.2 素数量, 个数和种类 案例

分析:

1. 多个独立小图形, 看素数量
2. 数量都是5个不能排除
3. 种类, 记下同种种类数量分布, 311, 221, 311, 221, 311, ?
4. 答案应符合221同种种类数量的分布, 只有B符合

111575708634_.pic.jpg

19.3 素数量, 相邻比较 案例

分析:

1. 多个独立小图形, 看素数量
2. 相邻比较, 相邻图形存在一个相同元素, 只有D符合

121575723073_.pic.jpg

19.4 素数量, 解题思维

1. 数个数, 数种类
2. 找相同(相邻有相同, 内部有相同)
   相同元素的位置
   相同元素的数量

131575723817_.pic.jpg

19.5 素数量, 部分数

识别: 生活化图形, 黑色粗线条图形

19.6 素数量, 部分数, 案例

分析:

1. 出现类似"&, $, !..."生活化图形, 考虑素数量, 部分数
2. 发现都是4部分组成, 选B

141575724471_.pic.jpg

19.7 素数量, 部分数, 案例

分析:

1. 出现生活化图形, 考虑素数量, 部分数
2. 发现246都是2部分组成, 135都是1部分组成

151575724646_.pic.jpg

19.8 黑色粗线条, 生活化图形, 小结

小结:

1. 属性规律: 先看属性规律 - 开闭
2. 数面: 出现 留白, 考虑数面
3. 部分数: 如果上面无规律, 考虑部分数

161575725855_.pic.jpg

19.9 数量规律 小结
面: 窟窿多, 图形被分割; 生活化, 粗线条图形留白
线: 多边形, 单一直线; 圆, 单一曲线; 笔画数, 多端点, 日田变形
点: 大树叉, 相切较多

171575725929_.pic.jpg

20. 空间

考点:

1. 正方体, 及其展开图的

20.1 正方体, 相对面

应用:
立体图中相对面不会同时出现, 相对面同时出现的选项 - 排除

展开图中如何判断相对面:

1. 同行或同列相隔一个面, 互为相对面
2. Z字形两端(这两端必须紧邻Z字中线), 互为相对面

11575792761_.pic.jpg

20.1.1 相对面,案例

分析:

1. A, B, D 相对面同时出现, 排除, 选C

21575792855_.pic.jpg

20.1.2 相对面,案例

分析:

1. A 相对面同时出现

31575793170_.pic.jpg

20.2 正方体, 相邻面-公共边

如何确定公共边:

1. 展开图中直接相邻的两个面的公共边
2. 展开图中构成直角的两个边是同一条边
3. 一排4个面, 两头的两条边是同一条边

技巧:

1. 确定面中图形与公共边的位置关系(指向, 垂直/平行)

20.2.1 公共边, 案例

分析:

1. 发现 "五角星" 面 与公共边有明显的特殊位置关系, 考虑先看公共边
2. ABD 与公共边的位置关系 错误, 排除

41575795232_.pic.jpg

20.2.2 相对面和公共边, 案例

分析:

1. A 相对面同时出现, 排除
2. B "小菱形" 应该平行于相邻面, 选项为垂直, 排除
3. D 公共边对应的相邻面错误, 且相对面同时出现, 排除

51575795862_.pic.jpg

20.3 正方体, 相邻面-公共点

识别:
立体图中, 三个面组成一个公共点

技巧: 公共点引出的线位置关系保持不变

20.3.1 正方体, 相对面-相邻面-公共点, 案例

分析:

1. A 三个面组成一个公共点, 找到展开图的公共点, 发现公共点没有引出直线, 排除A
2. C 相邻面对于公共边的位置关系错误, 排除
3. D 相邻面对于公共边的位置关系错误, 且相对面同时出现, 排除

61575796640_.pic.jpg

20.3.2 正方体, 相对面-相邻面-公共点, 案例

分析:

1. A 相邻面对于公共边的位置关系错误, 排除
2. C 相邻面对于公共边的位置关系错误,且公共点位置关系不对, 排除
3. D 相邻面对于公共边的位置关系错误, 排除

71575797021_.pic.jpg

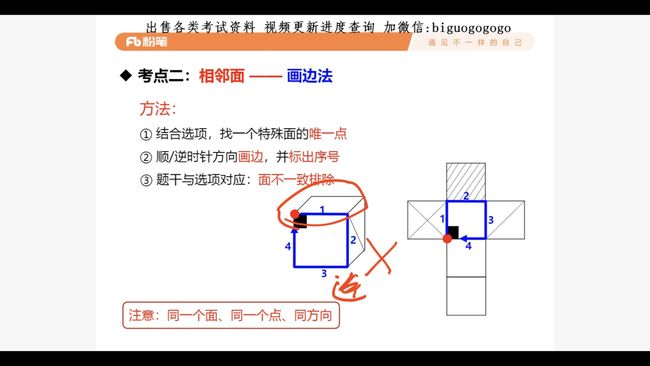
20.4 正方体, 相邻面 - 画边法

方法:

1. 结合选项, 找到一个特殊面的唯一点
2. 顺/逆时针方向画边, 并标出记号
3. 题干与选项对应, 面不一致的排除

11575852708_.pic.jpg

20.4.1 画边法, 案例

分析:

1. B 相对面同时出现, 相邻边图形位置错误, 排除
2. C 画边法可以排除, 且可以用相邻边图形发现位置错误
3. D 画边法可以排除, 且可以用相邻边图形发现位置错误

21575853328_.pic.jpg

20.4.1 公共点, 画边法, 案例

分析:

1. A 三个相邻面组成公共点, 公共点的相邻面相对位置保持不变, 不符合, 排除
2. B 三个相邻面组成公共点, 公共点的相邻面相对位置保持不变, 不符合, 排除
3. C 公共点无法排除, 用画边法, 发现相对位置错误, 排除

31575855206_.pic.jpg

20. 5 正方体, 小结

1. 无中生有, 直接排除
2. 判断位置关系
   2.1 相对面同时出现 -排除
   2.2 相邻面 - 公共边 - 图形与公共边的位置关系(指向, 垂直/平行)
   2.3 相邻面 - 公共点 - 图形与公共点为位置关系(顺逆时针顺序, 角度关系)
   2.4 画边法

41575855860_.pic.jpg

21. 总结

51575858321_.pic.jpg