前言
友情提示,这篇文章很长,光是滑动到底部就需要好几秒,请合理安排阅读时间。
最近在学习异常值探测(Outlier Detection)。
家里的书架上有一本叫《数据挖掘与R语言》的书,作者是Luís Torgo。这本书给出了用R做数据挖掘的四个案例,其中一个正好是欺诈交易探测。
这个案例给出的数据预处理过程非常棒,思路很值得学习,所以这部分我跟着案例,把处理过程自己实现了一遍。这篇文章的前半一部分是分享这个数据预处理过程。
在算法部分,作者给出了好几类不同的异常值探测方法。这篇文章的后半部分讨论其中一种探测方法(局部异常因子算法),及其分析效果。
顺带一提,这本书出得早(英文版出版于2011年,中文版出版于2012年),当时一些很elegant的R库还不成熟,作者在书中使用的代码比较旧,大家如果想照着案例把分析过程实现一遍,我个人觉得不需要完全按作者的代码走,太绕。
然后就是,作者并不是系统地介绍各个数据挖掘方法,而是围绕案例,把能用到的算法都聊一遍,我个人觉得不是很适合新手。(这本书是我在出国前买的,当时对数据挖掘的概念还很模糊,看这本书基本上是一头雾水。当然,现在依然还是不能全都看懂……)
另外,这本书的翻译实在是太一言难尽了,机械工业出版社一生黑,对这本书非常感兴趣的朋友,我极力推荐你们去看英文原版。
废话结束,以下是我关于这个分析案例的学习笔记。
数据预处理
0. 分析工具与数据来源
- 分析工具:R
- 主要用到的库:
tidyverse,ggplot2(作者没有用这些库,而是用R的基本库) - 数据来源:
library(DMwR)
data(sales)
1. 数据集
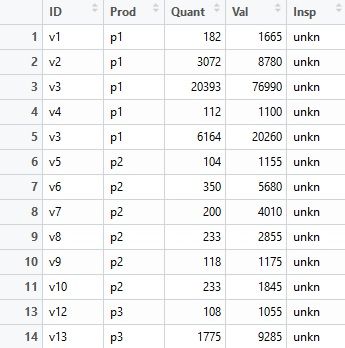
先来看看分析中使用的数据集。
上图是数据集的前14行。整个数据集一共有401146行。
这个数据集的每一行,表示一份关于某销售员销售某款产品的销售报告,具体特征包括:
- ID:销售员id,一个销售员可以销售多款产品。
- Prod:产品id,一款产品可以被多个销售员售卖。
- Quant:销售员上报的产品销售数量。
- Val:销售员上报的产品销售总额。
- Insp:报告标签。ok - 公司检查了该销售报告并认为其真实有效;fraud - 公司认为该报告为欺诈报告;unkn - 该报告未经过公司审查。
Insp是此次欺诈交易探测任务的目标特征,即,我们想要知道,在这些unkn的报告中,哪些是ok的哪些是fraud的。
2. 数据基本情况
明白数据集的基本构成之后,现在我们来进一步认识一下这份数据。
2.1 数据概述
先来summarize一下各个特征。
报告数量最多的销售员是v431,有10159份销售报告;报告谈及最多的产品是p1125,有3923份报告是关于它的;在产品销售量上,数据可能是right-skewed的,注意到平均数(mean)比中位数(median)要大很多;同理,在销售额上,数据也可能是right-tailed的;在报告标签方面,unkn比另两者在数量上要大很多。
另外,注意Quant和Val是有不少缺失值的(NA's)。既然有缺失值,那么不妨顺带看一下数据集中的缺失值有什么特点(Missing Pattern):
第2-5行、第2-6列中,1表示该特征无缺失值,0表示该特征有缺失值,由此可以得到4种不同的缺失值分布(最后一列的第2-5行):0 - 所有特征都没有缺失值,1 - 有一个特征存在缺失值,2 - 有两个特征存在缺失值。则,第一列表示该缺失值分布下的样本数,最后一行表示该特征的缺失值总数。
可以看到,在13842个Quant缺失的样本中,有12954个样本只在Quant这个特征上有缺失;在1182个Val缺失的样本中,有294个样本只在Val这个特征上有缺失;此外,共有888个样本,Quant和Val同时缺失。
2.2 Insp
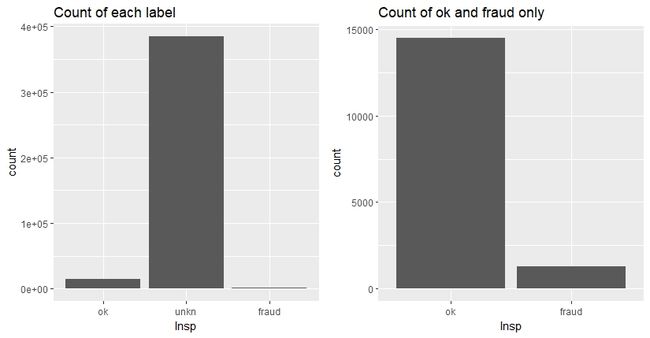
接着看一下目标特征Insp的分布情况。
左图是三类标签(ok、fraud、unkn)的数量分布,可以看到,unkn比另外两者要多很多(占96%)。
右图是去掉了unkn后,ok和fraud的数量分布图,ok和fraud样本的数量比约为11:1。
这个情况符合异常值的特性:在一份数据集中,异常值只占很少很少的一部分。(这同时也是异常值探测不那么容易做的原因,占比实在太小。)
2.3 ID & Prod
这个数据集中,有6016个不重复的销售员id和4548个不重复的产品id。
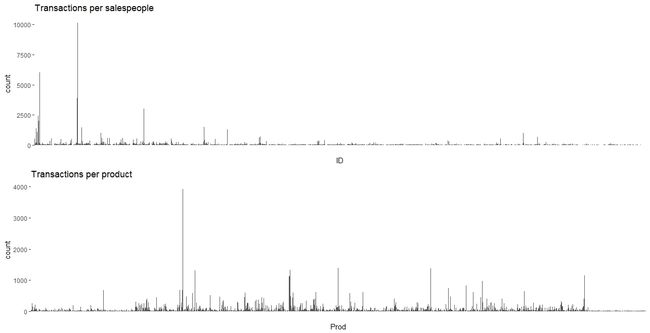
每个销售员id下的报告数和每款产品id下的报告数分布如下:
可以看到,数据分布很不均匀,有些销售员/产品下的报告总数明显远高于其他销售员/产品。
3. 构建新特征
3.1 产品单位价格
有销售总量Quant和销售总额Val,我们其实可以用Val/Quant来计算每份报告的产品单位价格。
Summarize一下这个新特征可以得到:
可以看到,最小产品单位价格为0,最大为26460,平均数(20.3)大于中位数(11.89),数据分布可能是right-skewed的。
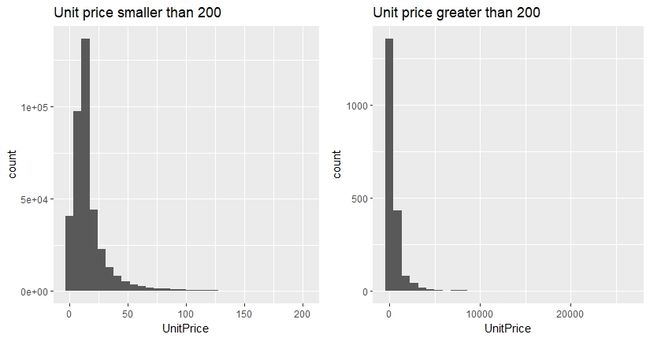
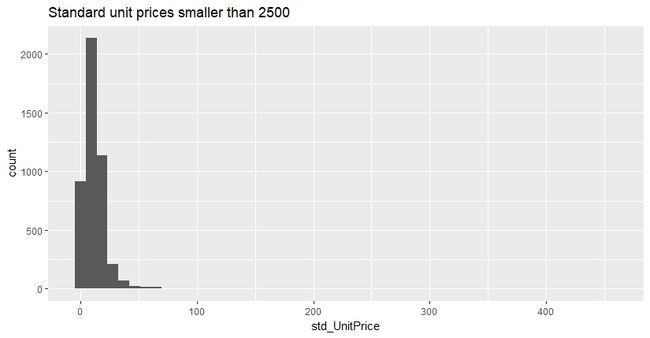
下面来具体看一下产品单位价格的分布情况:
为了更清晰地展现数据,我给单位价格小于200和大于200的数据分别做了直方图。
可以看到,数据非常的skewed。
3.2 产品标准价格
上述产品单位价格是每份报告中Val和Quant的比值,那么一款产品,在不同的报告中可能会有不同的产品单位价格(不同Val、Quant给出不同的比值)。
也就是说,每款产品对应一组产品单位价格数据。
在这种情况下,作者用每组单位价格的中位数来代表其对应产品的标准价格。
去掉极值(大于2500)的产品标准格分布如下:
可以看到产品标准价格同样是right-tailed的(median = 11.24,mean = 15.00)。
4. 基于Quant、Val、产品单位价格的极值对比
作者在案例中做了三组对比分析:
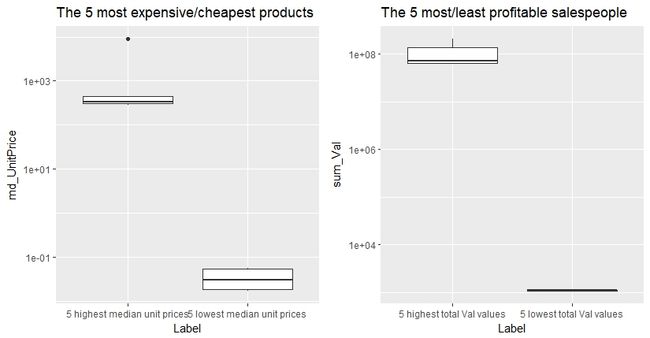
- 标准价格最高的5款产品 vs. 标准价格最低的5款产品
- 总销售收益额最高的5个销售员 vs. 总销售收益额最低的5个销售员
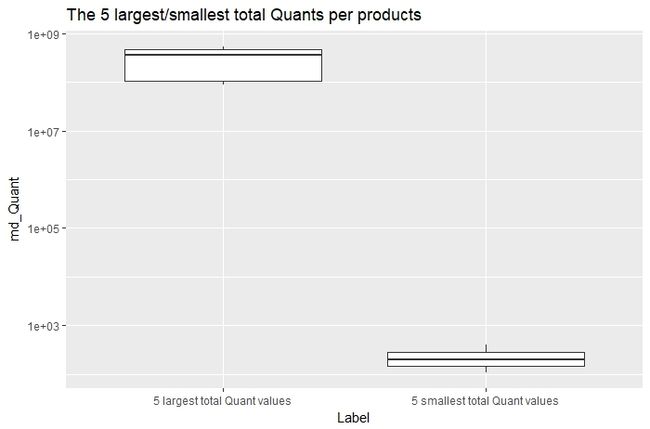
- 总销量最高的5款产品 vs. 总销售量最低的5款产品
这些对比是很好的BI分析,可以帮助公司管理团队做出有价值的决策。
上述三组对比通过箱型图展示如下:
可以看到,在每组对比中,最高的5个数据在数值上比最低的5个数据要高很多,说明公司的销售情况是极其不均的。
实际上,在销售员总销售收益额(sum of Vals per salesperson)方面,前100的销售员占了所有报告Val的总和的38%,后2000位销售员只占了2%。而在产品总销量上,前100的产品占了所有报告Quant的总和的75%,后4000个产品只占9%。
这样的比例构成说明公司其实可以精简产品线和销售员队伍。
我个人最喜欢这部分,缺少商业经验的analyst很难在一开始就想到要做这些方面的分析,至少我是被惊艳到了。
5. 缺失值处理
在缺失值的处理上,作者也分析得很细致,思路上值得学习(结论上有待进一步探讨)。
回顾一下前文,在所有有缺失值的样本中,有:
- 888个样本在Quant和Val上都有缺失
- 12954个样本只在Quant上有缺失
- 294个样本只在Val上有缺失
先来看那888个在Quant和Val上都有缺失的样本。这里主要是看每位销售员或每款产品的Quant和Val同时缺失的报告的占比。
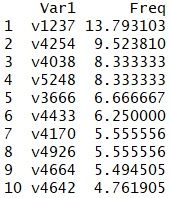
下图是Quant和Val同时缺失的报告占比最大的10位销售员:
这些缺失比例都不是很大,最大的只有14%左右。又考虑到,因为Quant和Val都缺失了,缺失值填补无从下手,所以作者认为可以把这些样本直接删除。
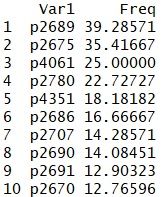
下图是Quant和Val同时缺失的报告占比最大的10款产品:
可以看到,有几款产品两个特征同时缺失的报告比例是比较大的,p2689有近40%的报告同时缺失Quant和Val数据。在这种情况下,作者认为用剩余报告去填补缺失信息(如用p2689剩余的60%的销售信息去填补其40%的缺失数据)是不合理的,所以这些报告也应该直接删除。(这部分的解释其实没有说服我,中文版翻译得乱七八糟,逻辑上我没有想透,先留个疑问在这里。)
接下来分析一下那12954份只在Quant上有缺失的样本。
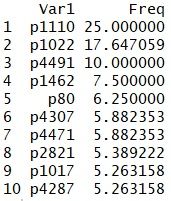
下图是仅Quant缺失的报告占比最大的10款产品:
p2442和p2443完全没有Quant的信息(缺失比例为100%),所以这两款产品的单位价格和标准价格都无法计算,也即无法进一步通过别的特征来填补这两款产品的Quant数据;此外,涉及p2442和p2443的一共有54份报告,其中2份标记为fraud,其余52份标记为ok,说明这两款产品已经被公司做过检测,暂时不需要进一步进行异常预测。因此,作者决定删除这54份报告。(其余报告保留。)
再看看仅Quant缺失的报告占比最大的10位销售员:
有5位销售员没有在他们的报告中填写Quant信息,但这些信息其实可以用Val/产品标准价格来填补(只要一款产品的Quant或Val不是完全缺失,其标准价格就可以被计算出来,那么某份报告缺失的Quant或Val就可以通过标准价格来计算),所以这些样本不删除。
最后来分析那294个只在Val上有缺失的样本。
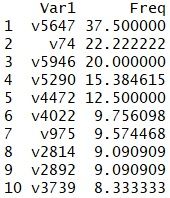
来看看仅Val缺失的报告占比最大的10款产品:
比例都不是很大,可以用产品标准价格*Quant来填补缺失的Val值。
最后看仅Val缺失的报告占比最大的10位销售员:
同理,可以用产品标准价格*Quant来填补这些缺失的Val值。
总结,在缺失值处理这部分:
- 删除888个在Quant和Val上均缺失的样本和54个涉及p2442、p2443的样本(完全没有Quant信息);
- 其余仅Quant有缺失的样本,通过
Val/产品标准价格来填补其Quant缺失值; - 其余仅Val有缺失的样本,通过
产品标准价格*Quant来填补其Val缺失值。
注意,这里的产品标准价格是剔除被标记为fraud的报告后,重新计算的产品标准价格。
缺失值处理后的数据集共有400204行。
异常值检测
进行完数据预处理之后,我们就可以开始运用具体算法进行异常值检测(在这个案例中,也称为欺诈交易探测),主要目的是找出那些在Quant或Val上有异常数值的报告,并对这些报告的异常程度进行排序(进而依据异常程度对这些报告依次进行人工核查)。
算法方面,作者在书中谈到的检测方法有:
- 无监督方法:基于箱图规则(i.e. 中位数、IQR)的探测方法,局部异常因子算法(Local Outlier Factor,LOF),基于聚类的离群值排名方法
- 有监督方法:简单贝叶斯,AdaBoost
- 半监督方法:自我训练模型
此外,作者没谈到但比较热门的无监督算法还有Isolation Forest。
这次的异常值探测我只选择了LOF算法。下面,我简单谈谈LOF,重点放在对LOF的理解和对其计算效果的讨论上。
1. 数据子集
我下面只用到了整个数据集的1%来做计算,原因是我用全部数据做计算的时候R给拒绝了,说数据量过大导致返回结果超出内存容量(40w+数据其实没有很大,可能是算法设计不高效导致了这个问题)。
另外,由于LOF是无监督方法,我个人的理解是在训练模型的时候不需要将数据集分为训练集和测试集(不一定正确),所以我没有做数据分割。
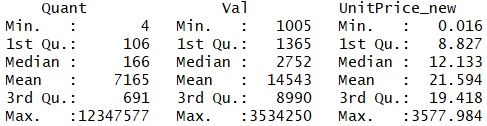
以下是用于运算的1%的数据子集的数据概述:
整个计算用到Quant、Val和产品标准价格3个特征,数据集不存在缺失值。
2. 局部异常因子算法(Local Outlier Factor,LOF)
LOF是一种基于距离的异常检测算法,其思想主要是:
- 通过比较每个点和其邻域点的密度来判断该点是否为异常点,点p的密度越低,越可能被认定是异常点;
- 密度通过点之间的距离来计算,点之间距离越远,密度越低,距离越近,密度越高;
- 因为LOF中,密度通过点的第k邻域来计算,而不是全局计算,因此得名“局部”异常因子。
算法计算过程的描述如下:
- 计算点p和其他点之间的距离;
- 确定第k距离和第k距离邻域;
- 计算点p的局部可达密度,即点p的第k邻域内点到p的平均可达距离的倒数;
- 计算点p的局部离群因子,即点p的邻域点的平均局部可达密度与点p的局部可达密度之比。
最终,通过各点的局部离群因子可以得到数据的异常值排序,某一点局的部离群因子数值越大(大于1),其越可能为异常值。
具体数学描述可以看这里。
3. 异常值检测结果
这里,我通过DMwR包的lofactor()函数调用LOF算法。且k取10。
3.1 基于原始特征的LOF异常值探测
首先,在不对特征进行任何处理的情况下,调用LOF做计算。
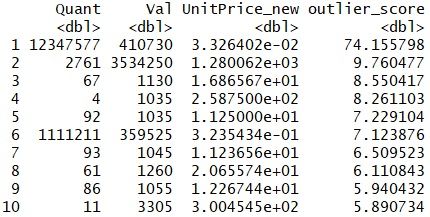
局部离群因子 Top 10 如下:
这些点的局部离群因子都大于5,其中排在第一位的点,其离群因子高达74.16。
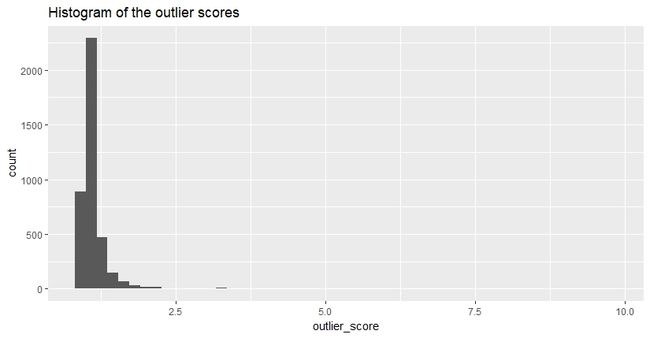
去掉局部离群因子最大点之后,各点局部离群因子的直方图如下:
可以看到,绝大部分点的局部离群因子小于2.5。
下面我们依据计算结果,对样本进行离散化:局部离群因子大于2.5的点被视为异常值,小于等于2.5的点为正常值。统计结果如下:
可以看到,所有点的局部离群因子的中位数为1.04;在所有被计算的点中,有45个点被视为异常点(局部离群因子大于2.5)。
值得注意的是,统计结果显示有10个点的计算结果为无穷值,有12个点的计算结果缺失。出现无穷值的原因可能是这些点的邻域内存在其他点与之重合,导致邻域点到该点的平均可达距离为0,从而该点局部可达密度无穷大,最终使得其局部离群因子无穷大。至于出现缺失值的原因,我暂时想不明白,可能是所调用的算法在设计上有bug?
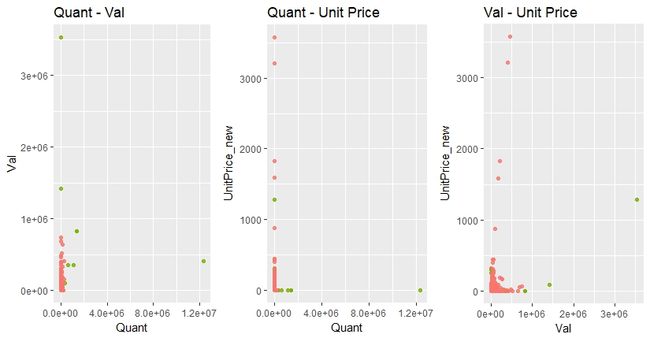
下面作散点图看一下LOF算法下的异常值(局部离群因子大于2.5)分布情况:
绿色表示异常点。
左边的图横轴为Quant,纵轴为Val。这张图中,所有远离左下角的点都被标为绿色,即这些极值点都被归为了异常点,这是我们想要看到的结果。
中间和右边这两张图的横轴分别为Quant和Val,纵轴都为产品标准价格。可以看到,这两张图中,有一些点的Quant或Val值在正常范围之内,但其产品标准价格却极高。这些点从直觉上来说并不正常,但其绝大多数并没有被标为绿色,即LOF算法没有将其归为异常点。这不符合预期。
对比上面这三张散点图可以发现,LOF能够较准确地识别Quant或Val异常的点,但却不能很好地辨别出产品标准价格异常的点。而回看我们的数据集,Quant和Val在数值上,比产品标准价格高了几个量级。
结合以上两点,我猜测LOF对特征的数值敏感。因此,我决定对Quant、Val、产品标准价格标准化,将它们的数值限定在(-1, 1)区间内,再对这些标准化后的特征进行LOF运算。
3.2 基于标准化特征的LOF异常值探测
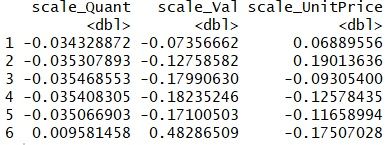
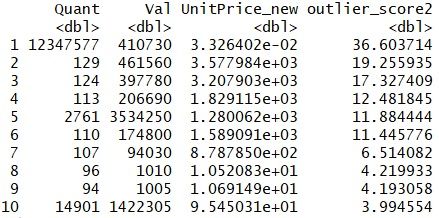
标准化后的Quant、Val、产品标准价格如下(前6行):
重新计算的局部离群因子 Top 10:
有6个点的局部离群因子大于10;排名第一的点,其局部离群因子为36.6。
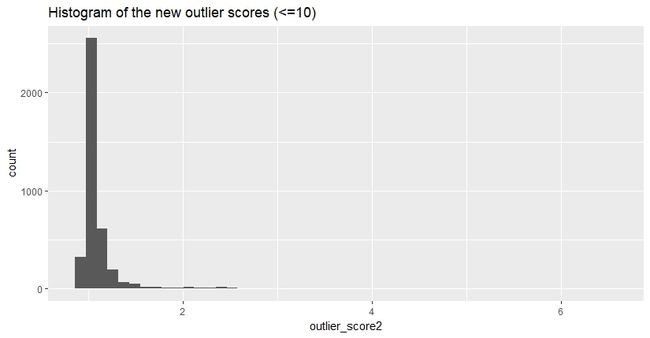
新的计算结果分布如下(排除了局部离群因子大于10的点):
绝大多数点的局部离群因子小于2.5。
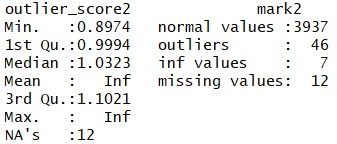
接下来我们依旧以2.5为临界值,对样本进行离散化:局部离群因子大于2.5的点被视为异常值,小于等于2.5的点为正常值。统计结果如下:
可以看到,所有点的局部离群因子的中位数为1.03;在所有被计算的点中,有46个点被视为异常点(局部离群因子大于2.5)。这一结果与之前结果相似。
这次计算中仍然存在无穷大值和缺失值。
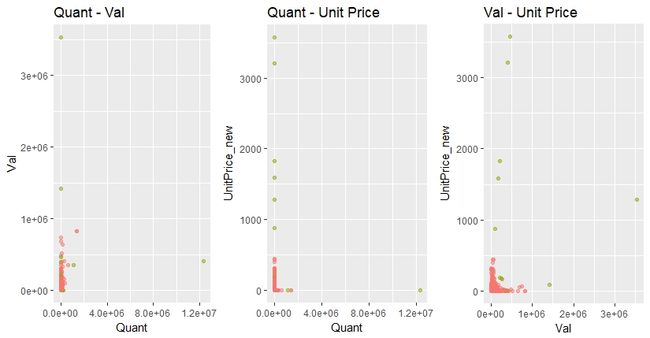
对新结果作散点图,可以得到如下异常值(局部离群因子大于2.5)分布情况:
绿色表示异常点。
可以看到,相比之前的结果,对标准化后的特征进行LOF计算,总体而言能更高效地识别出各个特征下的异常值。
以上。