浅谈数据结构和算法:广义表

一.定义

1.定义

广义表是线性表的推广,也有人称其为列表(lists,用复数的形式以示与统称的表list的区别)

2.表示形式

广义表一般记作 LS = (d1,d2,....,dn);
其中LS是广义表的名称,n是它的长度;
在线性表的定义中,ai(1<= i <= n)只限于是数据元素,而在广义表中,di可以是数据元素, 也可以是广义表,分别称为广义表的单元素和子集;
习惯上用大写字母表示广义表的名称,小写字母表示单元素;
当广义表非空时,称第一个元素d1为LS的表头(Head),称其余元素组成的表(d2,d3,......,dn)是LS的表尾;
广义表的定义是一个递归的定义,因为在描述广义表时又用到了广义表的概念;

3.广义表示例

A = () ----> A是一个空表,长度为0
B = (e) ---> B只有一个单元素e,长度为1
C = (a, (b, c, d)) ---> C有2个元素,分别是单元素a和字表(b,c,d),长度为2
D= (A, B, C) ---> D有3个元素,并且都是列表,将子表的值代入,则D = ((), (e), (a, (b, c, d)));
E = (a, E) ---> 这是一个递归的表,长度为2,E相当于一个无限循环的列表,E = (a, (a, (a, ...)))

4.列表相关结论

(1).列表的元素是子表,而子表的元素还可以是子表,因此列表是一个多层次的结构,可以用图表示列表,圆圈表示列表,方块表示单元素

列表的图形表示.png

(2).列表可为其他列表所共享, 例如3中 列表A B C是D的子表,则在D中可以不必列出子表的值,而是通过子表的名称来引用

(3).列表可以是一个递归的表,即列表也可以是其本身的一个子表,例如3中的E

5.列表基本操作 表头HEAD(LS)和表尾TAIL(LS)

(1).任何一个非空列表,其表头可能是单元素,也可能是列表,而其表尾必定为列表

例如 HEAD(B) = e, TAIL(B) = ()
HEAD(D) = A, TAIL(D) = (B, C)
由于(B, C)是非空列表,则可继续分解得到:
HEAD((B, C)) = B, TAIL((B, C)) = C

二.广义表的存储结构

1.由于广义表中的数据元素可以具有不同的结构(单元素或列表),因此难以用顺序存储结构表示,通常采用链式存储结构,每个数据元素可以用一个节点表示.
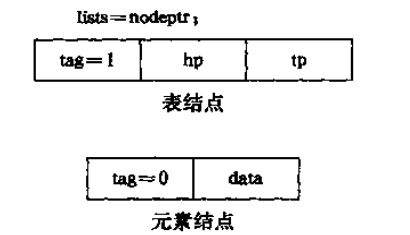
2.需要两种结构的节点:一种是表节点,用以表示列表,一种是元素节点,用以表示单元素.
3.上节得知,若列表不空,则可分解成表头和表尾;反之,一对确定的表头和表尾可唯一确定列表.
4.一个表节点可由三个域组成:标志域,指示表头的指针域和指示表尾的指针域
一个元素节点只需要两个域:标志域和值域

列表的节点表示.png

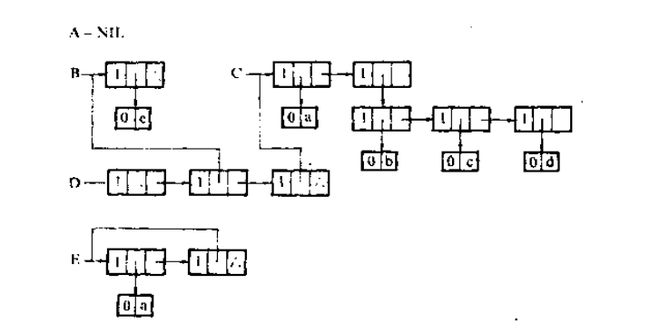
5.上节示例中,存储结构表示

列表示例的存储结构.png

由图得出相关结论:
(1).对任何非空列表,其表头指针均指向一个表节点,且该节点中的hp域指示列表表头(或为元素节点或为表节点),tp域指向列表末尾(除非表尾为空,则指针为空,否则必为表节点)
(2).容易分清列表中单元素和字表所在层次.
如在列表D中,单元素a和e在同一层次上,而b c d在同一层次且比a e低一层,B和C是同一层的子表
(3).最高层的表节点个数即为列表的长度
以上3个结论在某种程度上会给列表的操作带来方便