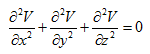计算物理第12次作业

Name: 贺一珺
Student Number: 2014302290002

Question

• 5.1 Solve for the potential in the prism geometry in Figure 5.4.
• 5.4 Investigate how the magnitude of the fringing field of a parallel plate capacitor, that is, the electric field outside the central region of the capacitor in Figure 5.6, varies as a function of the plate seperation.
• 5.6 Calculate the electric potential and field near a lightning rod. Model this as a very long and narrow metal rod held at a high voltage, with one end near a conducting plane. Of special interest is the field near the tip of the rod.
• 5.7 Write two progrems to solve the capacitor problem of Figure 5.6 and 5.7, one using the Jacobi method and one using the SOR algorithm. For a fixed accuracy compare the number of iterations, N_iter, that each algorithm requires as a function of the number of grid elements, L. Show that for the Jacobi method N_iter ~ L^2, while with SOR N_iter ~ L.

Abstract

In last chapter I calculated the trejectory of planets and analys several conditions that lead to chaos. In this chapter I will try to use python to solve several diffrential equations under different boundary conditions.
The potential in space satisfies the Laplace equation:

Laplace equation

Given specific boundary conditions, we can work out the eqaution analytically. However, the boundary conditions in the real world has never been that easy. Thus we need to find numberical ways to solve the problem. In this chapter we learned that in 2-dimensional cases, the whole space can be approximate as a net and the value on each point is the average of the volue of its surrending points.
In this homework, I will try to use Jacobi method, Gauss-Seidel method and simultaneous over-relaxation method which increase the speed of approximation.

Background

Relaxation (iterative method)

In numerical mathematics, relaxation methods are iterative methods for solving systems of equations, including nonlinear systems.

Relaxation methods were developed for solving large sparse linear systems, which arose as finite-difference discretizations of differential equations. They are also used for the solution of linear equations for linear least-squares problems and also for systems of linear inequalities, such as those arising in linear programming. They have also been developed for solving nonlinear systems of equations.

Relaxation methods are important especially in the solution of linear systems used to model elliptic partial differential equations, such as Laplace's equation and its generalization, Poisson's equation. These equations describe boundary-value problems, in which the solution-function's values are specified on boundary of a domain; the problem is to compute a solution also on its interior. Relaxation methods are used to solve the linear equations resulting from a discretization of the differential equation, for example by finite differences.

These iterative methods of relaxation should not be confused with "relaxations" in mathematical optimization, which approximate a difficult problem by a simpler problem, whose "relaxed" solution provides information about the solution of the original problem.

Jacobi method

In numerical linear algebra, the Jacobi method (or Jacobi iterative method) is an algorithm for determining the solutions of a diagonally dominant system of linear equations. Each diagonal element is solved for, and an approximate value is plugged in. The process is then iterated until it converges. This algorithm is a stripped-down version of the Jacobi transformation method of matrix diagonalization.

Gauss–Seidel method

In numerical linear algebra, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a linear system of equations. It is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel, and is similar to the Jacobi method. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is only guaranteed if the matrix is either diagonally dominant, or symmetric and positive definite.

Plotting

(For concenience, small changes of my code will not be shown here.)

5.1

Here is code1
Here is code2

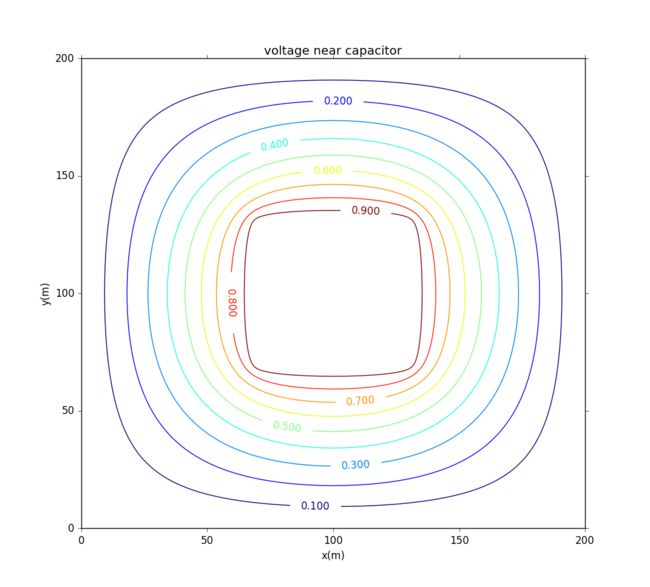
I use Gauss-Seidel to do this calculation and here I get the result:
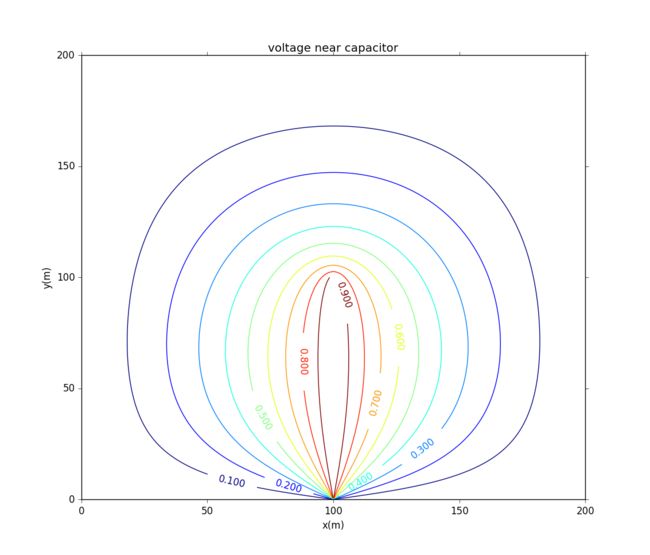
The potential is:

Electrical potential

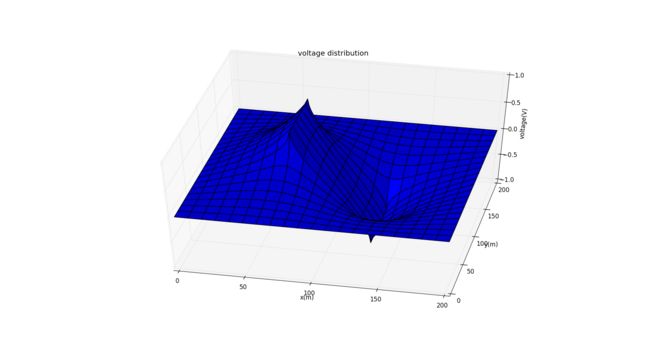
Here is the 3D picture:

3D plotting

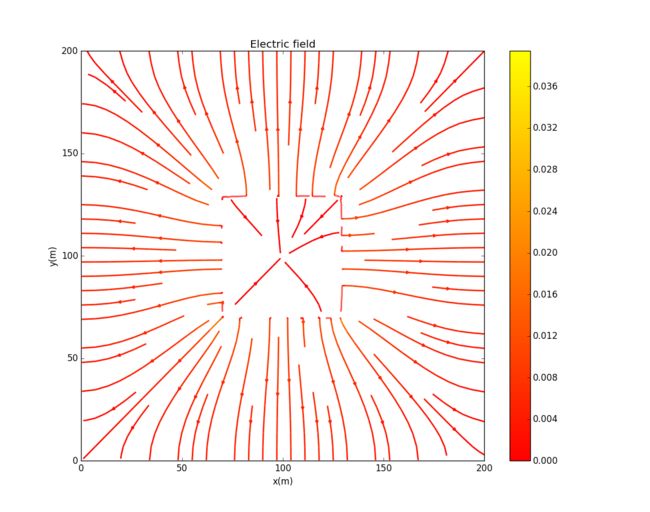
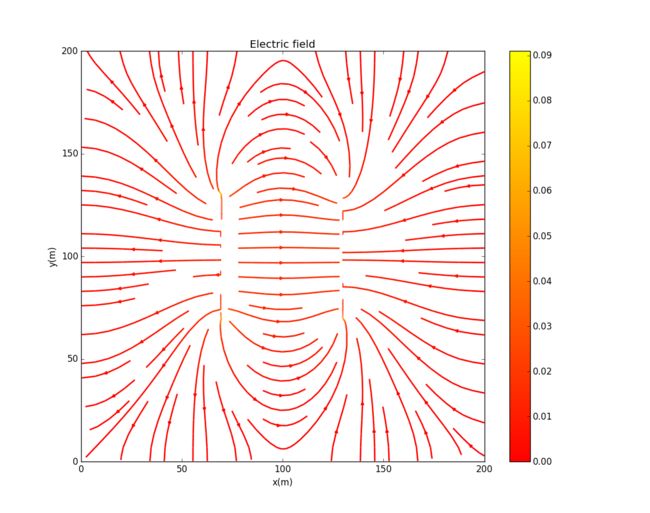
And here I get the electric field:

Electric field

5.4

Here is code

I use Gauss-Seidel to do this calculation and here I get the result:

Plate seperation: 0.6

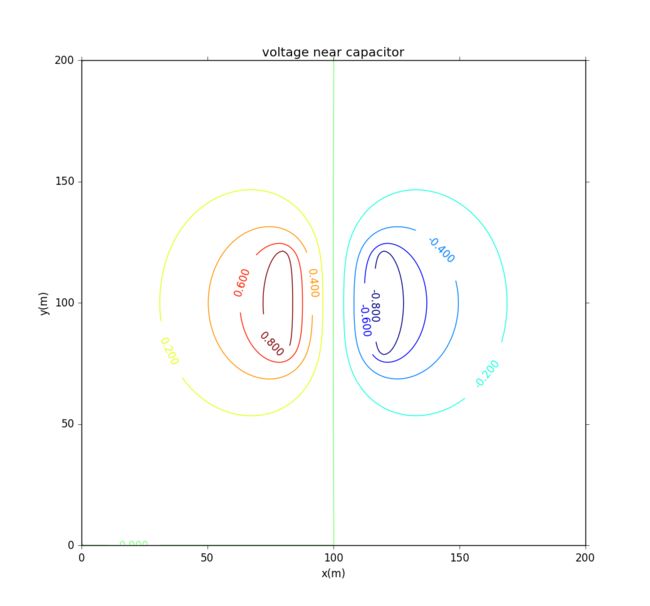
The potential is:

Electrical potential

Here is the 3D picture:

3D plotting

And here I get the electric field:

Electric field

Plate seperation: 0.4

Electrical potential

Here is 3D picture:

3D plotting

Plate seperation: 0.1

Here is electric potential:

potential

3D plotting:

3D plotting

Plate seperation: 0.5

Here is electric potential:

potential

Here is 3D picture:

3D plotting

5.6

Here is code1
Here is code2
Here is the electric potential:

Electric potential

Here is 3D picture:

3D plotting

Here is electric field:

Electric field

5.7

Here is code
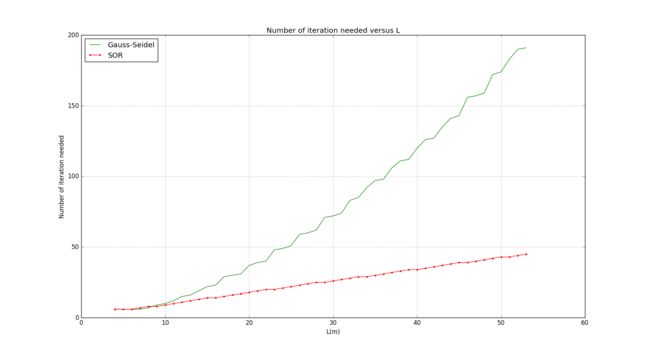
Now I will compare the G-S method and SOR method:

Comparasion

It can be easily concluded from this picture that the speed of converence of SOR method is significantly better than that of Gauss-Seidel method.

Acknowledgement

• Prof. Cai
• Yuqiao Wu
• wikipedia

How to contect me?

• Wechat ID: bestsola
• E-mail: [email protected]