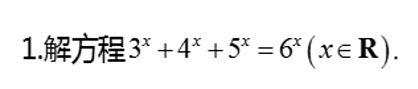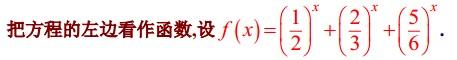沪江高中数学刘爱洁老师:江湖人称爱姐,沪江首席高中数学资深教师,北京科技大学数学系研究生。授课过程饱含激情又带有欢乐,只有亲身体验过才能知道其中的酸甜苦辣,所带学生单科成绩可进步20-80分,提倡快乐学习,爱上数学,变身数学学霸~
高考是一种博弈,一种较量,大多数孩子想出人头地只能通过高考的选拔,所以高考从来都不是轻松地。身处这场没有硝烟的战争,对手在身边又不在身边,对手是一起谈笑风生的同桌,也是素未谋面的其他考生。
而你要想胜出,需要靠实力,靠运气,更靠思想。一方面是心理思想。你要有强大的心理调节能力,才能坚持下来;另一方面也是做题思想。
高考数学,远不是只考查公式和计算就可以的。高考考察的是综合能力,知识+逻辑思维能力+灵活性。我们学习了3年高中数学,以下这7种做题思想才是我们在面对高考时的有用利器!
第一个思想:函数与方程思想
函数在高考中占比60%左右,所以函数可以说是高考的魂,高考的根基。函数思想是对于函数内容在更高层次上的抽象、概括与提炼,在研究数列、不等式、解析几何等方面有很重要的作用;那方程思想是解决各种计算问题的基本思想,是我们基本运算能力的必备。
咱们来看个例题,体会一下这个方法。
看得出来,用我们现有的知识,无法直接求解,也就只能带入几个常数试验一下看看能不能恰好得到一个解,但是这也是没有办法写过程的。所以我们必须用数学的思想方法转化成我们熟悉的方程问题。
首先考虑左右两边都存在指数函数,先化简一下,右边变为常数,左边变为可以用函数思想的部分。
从这个函数上可以看出,f(x)是单调递减的,进而通过验证法可以求解出x=3即为所求的解。所以只需要一步,题目就转化为了熟悉的函数问题。
第二个思想:数形结合思想
数形结合思想就是把问题的数量关系和图形结合起来考查的思想方法,即根据解决问题的需要,可以把数量关系的问题转化为图形的性质和特征去研究,或者把图形的性质问题转化为数量关系的问题去研究。这个思想从初中就开始使用,到高中是升华和爆发。
数形结合思想的应用主要体现在三个方面:
(1)数转化为形,即根据的“数”的特点,构造符合条件的几何图形,用几何方法解决。
(2)形转化为数,即根据题目特点,用代数方法去研究几何问题。
(3)数形结合,即用数研究形,用形研究数,相互结合,使问题变得简捷、直观、明了。
数形结合的应用最深的印象应该是在直线与圆的章节,比如
这些思路都将数学计算的问题转化为了图形问题。当然数形结合思想应用不仅仅局限于这些,它也活跃在函数、立体几何、圆锥曲线等知识中。
第三个思想:分类与整合思想
分类与整合思想,是一种重要的数学思想,也是一种重要的解题策略。它可以将整体化为局部,将复杂问题化为单一问题,以便于“各个击破”。但做题中要注意克服思维定势,处理好“分”与“合”,“局部”与“整体”之间的辩证统一关系,充分挖掘求解问题中潜在的特殊性与简单性,尽可能地简化或避免分类讨论。
一般,分类讨论主要是以下几个方面:
(1)所涉及的数学概念是分类进行定义的。
如|a|的定义分a>0、a=0、a<0三种情况。这种分类讨论题型可以称为概念型。
(2)涉及的数学定理、公式和运算性质、法则有范围或者条件限制,或者是分类给出的。
如等比数列的前n项和的公式,分q=1和q≠1两种情况,可以称为性质型。
(3)解含有参数的题目时,必须根据参数的不同取值范围进行讨论。
如解不等式ax>2时分a>0、a=0和a<0三种情况讨论。这称为含参型。
(4)某些不确定的数量、不确定的图形的形状或位置、不确定的结论等,都主要通过分类讨论,保证其完整性,使之具有确定性。
剩下的4种等同学们消化消化~明天同一时间,来找小编哟~~
如有任何疑问,欢迎加入【爱数学-学霸QQ群】513299807,和老师同学一起探讨,还可以领取更多高中数学提分资料。加群请标明来源于“”哦!
网友热搜:高考 高考辅导 高考复习 高考数学