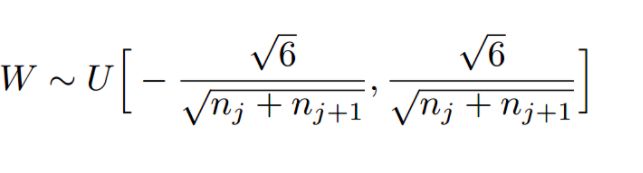这个例子可以说是caffe的入门之作,但里面包含的CNN知识已经十分丰富,值得入门者深深思考,会发现其中的很多美妙之处。
写这篇文章来记录自己的学习之旅。
首先这个例子的结构: lenet(模型)+mnist(数据)
其中mnist数据主要由两个函数处理:
1.下载二进制文件:
cd caffe ./data/mnist/get_mnist.sh
下载下来的文件有四个:
2.将这些二进制文件转换为caffe支持的LEVELDB或者LMDB:
$./examples/mnist/create_mnist.sh
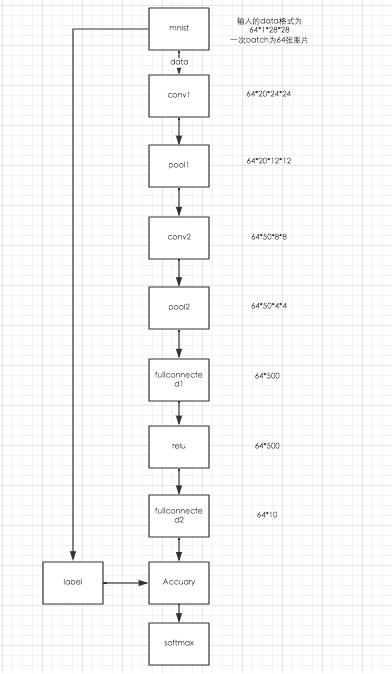
Lenet结构:
lenet结构简单,但是已经具备了一个CNN网络最基本的具备的元素了。以下为它的训练结构:
其中,图片经卷积后输出大小的计算公式为:
原图:N*N
fliter: F*F
stride:S
padding:P
输出的图片大小为M*M M= (N-F+2P/S+1
注意这里的不适用 :不同方向上不同stride以及padding的卷积。
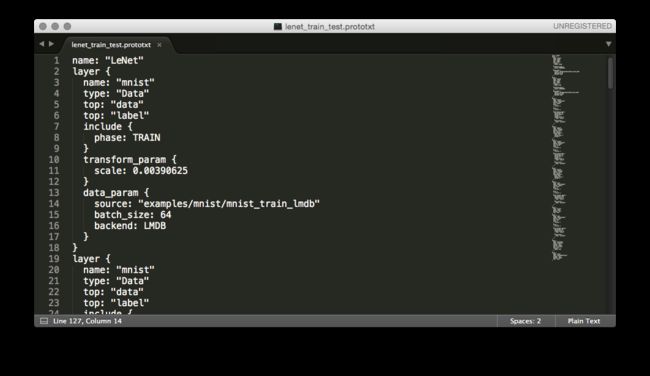
那么caffe是如何定义这个模型的:在caffe中模型的描述文件为example/mnist/data/lenet_train_val.prototxt,正是caffe的依赖包:protobuffer将模型的定义读取到内存中。
我们来看一看这个文件:
很容易看懂,caffe层的定义和积木一样,很清楚说明上一层是什么,下一层是什么,
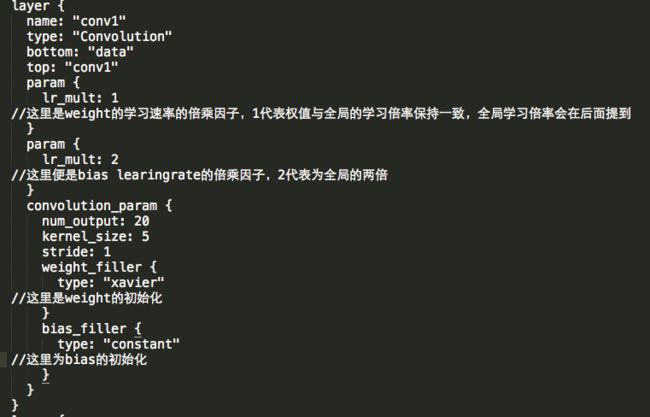
让我感兴趣的是卷积层的定义:
其中,weight的初始化使用了xavier填充器,
“Xavier”初始化方法是一种很有效的神经网络初始化方法,是由Xavier Glorot 和 Yoshua Bengio在2010提出的,第一次接触到这个是在自编码器的权值初始化看到的:
使用原因:
如果深度学习模型的权重初始化得太小,那么信号在每层间传递时将会逐渐缩小而难以产生作用,而如果初始化得太大,那信号将在每一层传递时逐渐过度放大而最终发散失效。
Xavier初始化目的就为了初始化深度学习网络时让权重不大不小,具体得推导过程以后专门写一篇。
简单来说:主要为了使得权值的分布符合:
上面的话是lenet的基本模型,而具体训练的话仍需要我们另外定义的超参数:
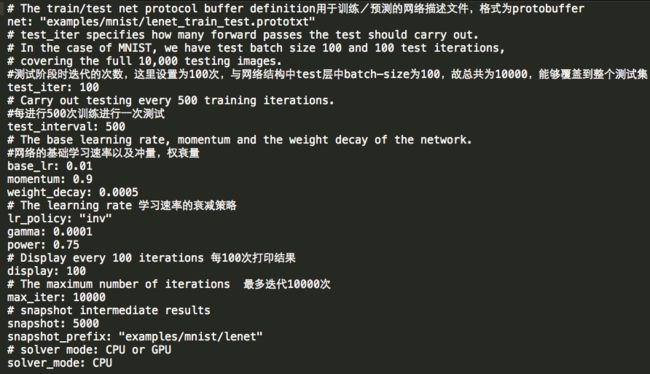
训练模型的超参数存于 ./example/mnist/lenet_solver.prototxt
我们来看一看里面的内容:
首先很明显这里使用了SGD的优化方法,故对于每个batch,loss函数应为:
根据dataloss的不同定义,以及正则化方式选择的不同,展开式子也不同。这个部分以后也会写一篇文章来记录下已经学过的内容。
SGD的最普通式子:
caffe 这里用到是:
很有趣有人说是受了牛顿的启发,加入这个m(monentum),为寻优加入了惯性的影响,所以当梯度下降的时候,在误差平面存在平坦区的时候,SGD能更快学习。以后将会好好研究
另一个有趣的是学习速率的衰减策略:
这里使用的是inv,且gamma设置为0.0001,power为0.75
所用公式为:base_lr= base_lr *(1+gamma*iter)^(power)
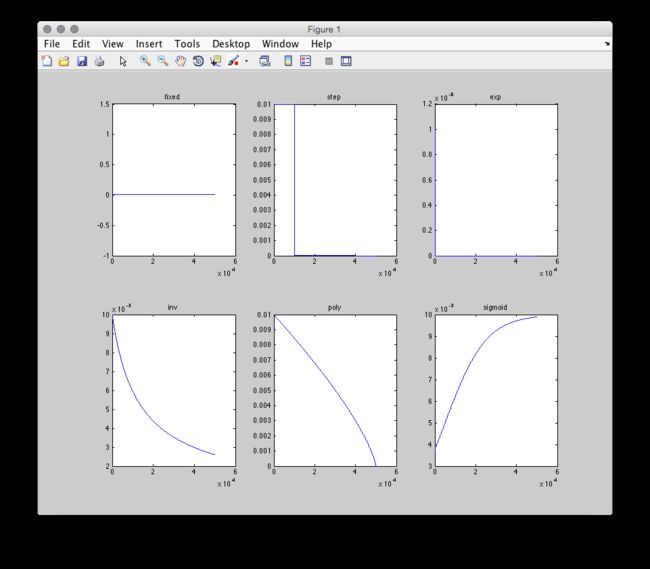
caffe同时提供了其他的学习速率改变方法:
// - fixed: always return base_lr.
// - step: return base_lr * gamma ^ (floor(iter / step))
// - exp: return base_lr * gamma ^ iter
// - inv: return base_lr * (1 + gamma * iter) ^ (- power)
// - multistep: similar to step but it allows non uniform steps defined by
// stepvalue
// - poly: the effective learning rate follows a polynomial decay, to be
// zero by the max_iter. return base_lr (1 - iter/max_iter) ^ (power)
// - sigmoid: the effective learning rate follows a sigmod decay
// return base_lr ( 1/(1 + exp(-gamma * (iter - stepsize))))
在matlab绘图中得到:
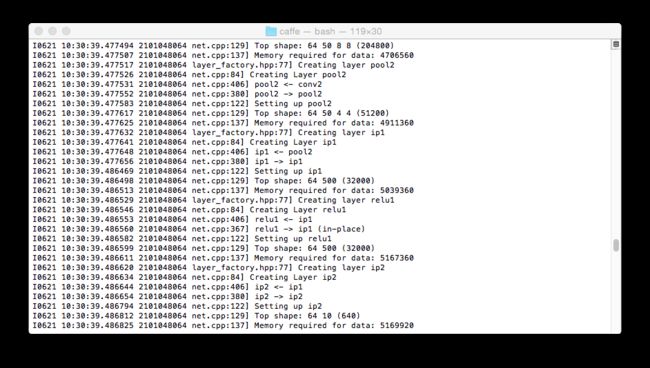
训练开始:
$./examples/mnist/train_lenet.sh
建立,迭代10000次,下面为输出
最后的模型快照存于caffe/examples/mnist/下