NOIP训练营内部试题-数数(树形DP+倍增)
摘要:
本文清北学堂NOIP训练营试题T3试题。
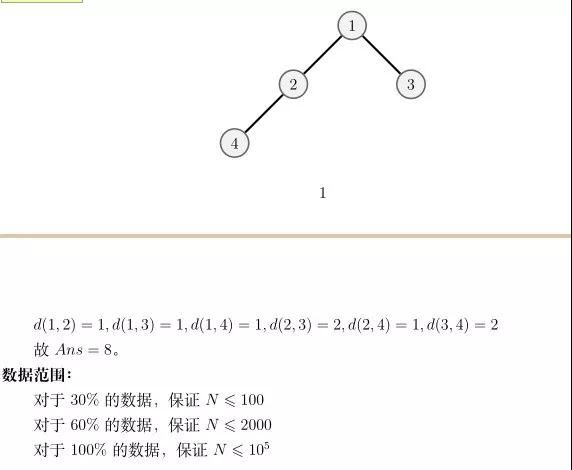
样例读入:
4
1 2
1 3
2 4
样例输出:
8
样例解释:
#include
#include
#include
#include
#include
#include
#include
#define st first
#define nd second
using namespace std;
struct edge {
int x;
int nxt;
};
typedef long long LL;
const int N = 1E5 + 10;
edge e[2 * N];
int lca[N][17], hd[N], fa[N], sons[N], nxt[N], cnt[N][17], f[N][17];
int n, m, x, y, l;
LL ans;
void link(int x, int y) {
e[++l].x = y;
e[l].nxt = hd[x];
hd[x] = l;
}
void dfs_lca(int x) {
lca[x][0] = fa[x];
sons[x] = 1;
for (int i = 1; i <= 16; ++i)
lca[x][i] = lca[lca[x][i - 1]][i - 1];
for (int p = hd[x]; p; p = e[p].nxt)
if (e[p].x != fa[x]) {
fa[e[p].x] = x;
dfs_lca(e[p].x);
sons[x] += sons[e[p].x];
}
}
void dfs_ans(int x) {
for (int p = hd[x]; p; p = e[p].nxt)
if (e[p].x != fa[x]) nxt[x] = e[p].x,
dfs_ans(e[p].x);
for (int i = 0; i <= 16; ++i) {
ans += sons[lca[x][i]] -
sons[nxt[lca[x][i]]];
if(sons[lca[x][i]] - sons[nxt[lca[x][i]]])
printf("%d :
sons[%d]-sons[%d]=%d\n",x,lca[x][i],nxt[lca[x][i]],sons[lca[x][i]] -
sons[nxt[lca[x][i]]]);
cnt[lca[x][i]][i]++;
f[lca[x][i]][i]++;
}
for (int i = 1; i <= 16; ++i)
for (int j = 0; j <= i - 1; ++j) {
ans += LL(cnt[x][i] +
f[x][i]) * LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]);
if(LL(cnt[x][i] + f[x][i]) *
LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]))
printf("%d :
cnt[%d][%d]+f[%d][%d] * sons[%d]-sons[%d] =
%I64d\n",x,x,i,x,i,lca[x][j],nxt[lca[x][j]],LL(cnt[x][i] + f[x][i]) *
LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]));
cnt[lca[x][j]][j] += cnt[x][i];
f[lca[x][j]][j] += f[x][i] +
cnt[x][i];
}
}
int main() {
//freopen("bitcount.in", "r", stdin);
//freopen("bitcount.out", "w",
stdout);
scanf("%d", &n);
for (int i = 1; i < n; ++i) {
scanf("%d%d", &x, &y);
link(x, y);
link(y, x);
}
dfs_lca(1);
sons[0] = sons[1];
nxt[0] = 1;
dfs_ans(1);
printf("%I64d\n", ans);
}
解析:
树形DP+倍增
回想倍增法求LCA的过程
从大到小枚举k,每次跳2^k步,只要不越界就跳,最后一定能跳到LCA
因为跳的都是2的幂次步,所以每跳一步就是二进制加了一个1
先预处理fa[i][k],表示点i向上跳2^k 步的祖先节点
设 f[i][j] 表示最后一步跳了2^j步,跳到了点i的答案之和
cnt[i][j] 表示最后一步跳了2^j步,跳到了点i的方案数
因为有了倍增求lCA原理的保证,所以只需要考虑跳2的幂次步
设siz[i]表示以i为根的子树的大小
rt[i]=j 表示 当前点属于 i的子树里,以j为根节点的子树
假设dfs回溯到x,转移分两种:
1、以x为链的一个端点
枚举x向上跳2^k次,则v=fa[x][j]
那么ans+=siz[v]-siz[rt[v]] ——所有非rt[v]子树的点,与x的LCA都是v,都会有1的贡献
(类似于点分治中要去除同一子树内合法的点)
cnt[v][k]++ f[v][k]++
2、x作为倍增过程中的一个中途点
那么枚举最后一步跳了2^i 跳到了x
枚举x再往上跳2^j步,则v=fa[x][j]
那么ans+=(f[x][i]+cnt[x][i])*(siz[v]-siz[rt[v]])
f[x][i] 是原来的答案,在以v做LCA时,又会用 (siz[v]-siz[rt[v]])次
cnt[x][i] 是 要再往上跳2^j步,又有一个1的贡献
cnt[v][j]+=cnt[x][i] f[v][j]+=f[x][i]+cnt[x][i]
例:1--2--3--4 如果4到1的距离为3,二进制为11,对答案的贡献为2
回溯到4的时候,以4为端点会累积3--4 2--4
回溯到3的时候,以3为端点会累积2--3 1--3
回溯到2的时候,以2为端点会累积1--2,以2为中途点会累积1--2--3--4
(4跳2^1累积到2里,然后在枚举2为中途点时,最后一步跳了2^1到2,2再往上跳2^0)
为什么在枚举3作为中途点的时候,不枚举跳了2^0次方到了3
因为此时3不是中途点,我们是按跳2^k,k是降序跳的
个人总结:支持本题不重不漏的原理就是倍增求LCA的原理
或者是说任意数可以拆为2^k1+2^k2+2^k3…… ki 依次递减
本文解析作者:xxy
出处:http://www.cnblogs.com/TheRoadToTheGold/