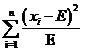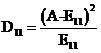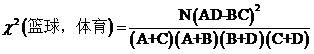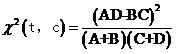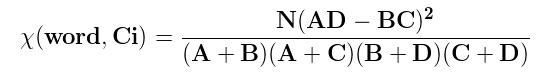卡方检验最基本的思想就是通过观察实际值与理论值的偏差来确定理论的正确与否。具体做的时候常常先假设两个变量确实是独立的(行话就叫做“原假设”),然后观察实际值(也可以叫做观察值)与理论值(这个理论值是指“如果两者确实独立”的情况下应该有的值)的偏差程度,如果偏差足够小,我们就认为误差是很自然的样本误差,是测量手段不够精确导致或者偶然发生的,两者确确实实是独立的,此时就接受原假设;如果偏差大到一定程度,使得这样的误差不太可能是偶然产生或者测量不精确所致,我们就认为两者实际上是相关的,即否定原假设,而接受备择假设。
那么用什么来衡量偏差程度呢?假设理论值为E(这也是数学期望的符号哦),实际值为x,如果仅仅使用所有样本的观察值与理论值的差值x-E之和
来衡量,单个的观察值还好说,当有多个观察值x1,x2,x3的时候,很可能x1-E,x2-E,x3-E的值有正有负,因而互相抵消,使得最终的结果看上好像偏差为0,但实际上每个都有偏差,而且都还不小!此时很直接的想法便是使用方差代替均值,这样就解决了正负抵消的问题,即使用
这时又引来了新的问题,对于500的均值来说,相差5其实是很小的(相差1%),而对20的均值来说,5相当于25%的差异,这是使用方差也无法体现的。因此应该考虑改进上面的式子,让均值的大小不影响我们对差异程度的判断
上面这个式子已经相当好了。实际上这个式子就是开方检验使用的差值衡量公式。当提供了数个样本的观察值x1,x2,……xi,……xn之后,代入到式(1)中就可以求得卡方值,用这个值与事先设定的阈值比较,如果大于阈值(即偏差很大),就认为原假设不成立,反之则认为原假设成立。
在文本分类问题的特征选择阶段,我们主要关心一个词word(一个随机变量)与一个类别Ci(另一个随机变量)之间是否相互独立?如果独立,就可以说词word对类别Ci完全没有表征作用,即我们根本无法根据word出现与否来判断一篇文档是否属于Ci这个分类。但与最普通的卡方检验不同,我们不需要设定阈值,因为很难说词word和类别Ci关联到什么程度才算是有表征作用,我们只想借用这个方法来选出一些最最相关的即可。
此时我们仍然需要明白对特征选择来说原假设是什么,因为计算出的卡方值越大,说明对原假设的偏离越大,我们越倾向于认为原假设的反面情况是正确的。我们能不能把原假设定为“词word与类别Ci相关“?
所以我们一般都使用”词word与类别Ci不相关“来做原假设。选择的过程也变成了为每个词计算它与类别Ci的卡方值,从大到小排个序(此时开方值越大越相关),取前k个就可以。
比如说现在有N篇文档,其中有M篇是关于体育的,我们想考察一个词“篮球”与类别“体育”之间的相关性(任谁都看得出来两者很相关,但很遗憾,我们是智慧生物,计算机不是,它一点也看不出来,想让它认识到这一点,只能让它算算看)。我们有四个观察值可以使用:
1.包含“篮球”且属于“体育”类别的文档数,命名为A
2.包含“篮球”但不属于“体育”类别的文档数,命名为B
3.不包含“篮球”但却属于“体育”类别的文档数,命名为C
4.既不包含“篮球”也不属于“体育”类别的文档数,命名为D
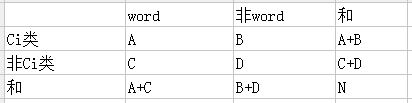
用下面的表格更清晰:
下面我们需要根据上面数据估算上面的ABCD四个值,根据估算值计算卡方值
对于A的估计值(上文说的是理论值):
A+B+C+D=N
A+C的意思其实就是说“属于体育类的文章数量”,因此,它就等于M,同时,B+D就等于N-M。
好,那么理论值是什么呢?以包含“篮球”且属于“体育”类别的文档数为例。如果原假设是成立的,即“篮球”和体育类文章没什么关联性,那么在所有的文章中,“篮球”这个词都应该是等概率出现,而不管文章是不是体育类的。这个概率具体是多少,我们并不知道,但他应该体现在观察结果中(就好比抛硬币的概率是二分之一,可以通过观察多次抛的结果来大致确定),因此我们可以说这个概率接近
(因为A+B是包含“篮球”的文章数,除以总文档数就是“篮球”出现的概率,当然,这里认为在一篇文章中出现即可,而不管出现了几次)而属于体育类的文章数为A+C,在这些个文档中,应该有
篇包含“篮球”这个词(数量乘以概率)。
但实际有多少呢?考考你(读者:切,当然是A啦,表格里写着嘛……)。
此时对这种情况的差值就得出了(套用式(1)的公式),应该是
同样,我们还可以计算剩下三种情况的差值D12,D21,D22。有了所有观察值的差值,就可以计算“篮球”与“体育”类文章的开方值
把D11,D12,D21,D22的值分别代入并化简,可以得到
词word与类别Ci的卡方值更一般的形式可以写成
接下来我们就可以计算其他词如“排球”,“产品”,“银行”等等与体育类别的开方值,然后根据大小来排序,选择我们需要的最大的数个词汇作为特征项就可以了。
实际上式(2)还可以进一步化简,注意如果给定了一个文档集合(例如我们的训练集)和一个类别,则N,M,N-M(即A+C和B+D)对同一类别文档中的所有词来说都是一样的,而我们只关心一堆词对某个类别的开方值的大小顺序,而并不关心具体的值,因此把它们从式(2)中去掉是完全可以的,故实际计算的时候我们都使用
针对英文纯文本的实验结果表明:作为特征选择方法时,开方检验和信息增益的效果最佳(相同的分类算法,使用不同的特征选择算法来得到比较结果);文档频率方法的性能同前两者大体相当,术语强度方法性能一般;互信息方法的性能最差。
但卡方检验也并非就十全十美了。回头想想A和B的值是怎么得出来的,它统计文档中是否出现词word,却不管word在该文档中出现了几次,这会使得他对低频词有所偏袒(因为它夸大了低频词的作用)。甚至会出现有些情况,一个词在一类文章的每篇文档中都只出现了一次,其开方值却大过了在该类文章99%的文档中出现了10次的词,其实后面的词才是更具代表性的,但只因为它出现的文档数比前面的词少了“1”,特征选择的时候就可能筛掉后面的词而保留了前者。这就是开方检验著名的“低频词缺陷“。因此开方检验也经常同其他因素如词频综合考虑来扬长避短。
总结
如图:
原假设:词word与类别Ci不相关
A:Ci类中word出现的次数
B:Ci类中没有出现word的次数
C:其他类出现word的次数
D:其他类没有出现word的次数
N:总文件数
根据上面的流程先分别计算ABCD的估算值(理论值)在计算其卡方值,再求和
则卡方值是:
卡方值越大,说明对原假设的偏离越大,我们越倾向于认为原假设的反面情况是正确的:word和Ci类相关
在上面的计算过程可以发出我们计算的是word属于Ci类的卡方值,当有多类的时候怎么办?
一般选取word对于Ci类的最大的卡方值,选取平均值效果比较差
选取较大的K个word作为文档的特征。
附:给精通统计学的同学多说几句,式(1)实际上是对连续型的随机变量的差值计算公式,而我们这里统计的“文档数量“显然是离散的数值(全是整数),因此真正在统计学中计算的时候,是有修正过程的,但这种修正仍然是只影响具体的开方值,而不影响大小的顺序,故文本分类中不做这种修正。
当特征w和主题类C之间完全独立的时候,x2统计量为0。x2统计量和互信息的差别在于它是归一化的统计量,但是它对低频特征的区分效果也不好。X2统计得分的计算有二次复杂度,相似于互信息和信息增益。在X2统计和互信息之间主要的不同在于X2是规格化评价,因而X2评估分值对在同类中的词是可比的,但是X2统计对于低频词来说是不可靠的。
利用x2统计方法来进行特征抽取是基于如下假设:在指定类别文本中出现频率高的词条与在其他类别文本中出现频率比较高的词条,对判定文档是否属于该类别都是很有帮助的.
采用x2估计特征选择算法的准确率在实验中最高,其分类效果受训练集影响较小,比较稳定。而且在对文教类和政治类存在类别交叉现象的文本进行分类时,采用x2估计的分类系统表现出了优于其它方法的分类性能。X2估计的可靠性较好,便于对程序的控制,无需因训练集的改变而人为的调节特征阀值的大小。
来源1:http://www.blogjava.net/zhenandaci/archive/2008/08/31/225966.html
来源2:http://blog.csdn.net/tvetve/article/details/2292111