七种排序的比较

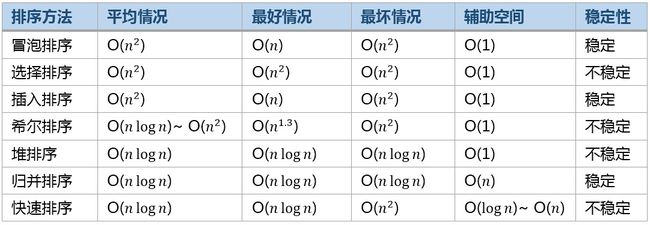
冒泡排序

原理：两两比较，不符合要求就调换位置。
代码：

function bubble() {
    var change;
    var sort = [3, 6, 4, 9, 13, 2, 1];
    for (var i = 0; i < sort.length - 1; i++) { 
        for (var j = i; j < sort.length; j++) {
            if (sort[i] > sort[j]) {
                change = sort[i];
                sort[i] = sort[j]
                sort[j] = change;
            }    
        }
        console.log(sort)
    }
}
bubble()

效果截图：

bubble.png

选择排序

原理：在未排序序列中找到最小元素，存放到排序序列的起始位置。
代码：

function selection() {
    var change;
    var sort = [3, 6, 4, 9, 13, 2, 1];
    for (var i = 0; i < sort.length; i++) {
        var min = i;
        for (var j = i + 1; j < sort.length + 1; j++) {
            if (sort[min] > sort[j]) {
                change = sort[min];
                sort[min] = sort[j]
                sort[j] = change;
            }
        }
        console.log(sort)
    }
}
selection()

效果截屏：

selection.png

插入排序

原理：对于每个未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
代码：

function swap(array, i, j) {
    var temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}
function insertion() {
    var sort=[3, 6, 4, 9, 13, 2, 1]
    var length = sort.length;
    for (var i = 1; i < length; i++) {
        for (var j = i; j > 0; j--) {
            if (sort[j - 1] > sort[j]) {
                swap(sort, j - 1, j);
            } else {
                break;
            }
        }
        console.log(sort)
    }
}

insertion();

效果截屏：

insertion.png

希尔排序

原理：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。
代码：

function shell() {
    var sort = [9,8,7,6,5,4,3,2,1,0];
    var len = sort.length;
    gap = Math.floor(len / 2);
    while (gap !== 0) {
        for (var i = gap; i < len; i++) {
            var temp = sort[i];
            var j;
            for (j = i - gap; j >= 0 && temp < sort[j]; j -= gap) {
                sort[j + gap] = sort[j];
                console.log(sort+'A')
            }
            sort[j + gap] = temp;
            // console.log(sort+"B")

        }
        gap = Math.floor(gap / 2);
        console.log(sort+'C');
    }
}
shell();

效果截屏：

shell.png

归并排序

原理：先考虑合并两个有序数组，基本思路是比较两个数组的最前面的数，谁小就先取谁，取了后相应的指针就往后移一位。然后再比较，直至一个数组为空，最后把另一个数组的剩余部分复制过来即可。

代码：

function merge(left, right) {
    var result = [];
    while (left.length && right.length) {
        if (left[0] < right[0])
            result.push(left.shift());
        else
            result.push(right.shift());
    }
    console.log(result.concat(left, right))
    return result.concat(left, right);
}

function mergeSort(a) {
    if (a.length === 1)
        return a;

    var work = [];

    for (var i = 0, len = a.length; i < len; i++)
        work.push([a[i]]);

    work.push([]); // 如果数组长度为奇数

    for (var lim = len; lim > 1; lim = (lim + 1) / 2) {
        for (var j = 0, k = 0; k < lim; j++, k += 2)
            work[j] = merge(work[k], work[k + 1]);

        work[j] = []; // 如果数组长度为奇数
    }
    return work[0];
}

console.log(mergeSort([9,8,7,6,5,4,3,2,1,0]));

效果截屏：

merge.png

快速排序

原理：从数列中挑出一个元素作为基准数，将比基准数大的放到右边，小于或等于它的数都放到左边，递归执行，直至各区间只有一个数。
代码：

function quickSort(arr) {
    if (arr.length <= 1) {
        return arr;//如果数组只有一个数，就直接返回；
    }

    var num = Math.floor(arr.length / 2);//找到中间数的索引值，如果是浮点数，则向下取整
    var numValue = arr.splice(num, 1);//找到中间数的值
    var left = [];
    var right = [];

    for (var i = 0; i < arr.length; i++) {
        if (arr[i] < numValue) {
            left.push(arr[i]);//基准点的左边的数传到左边数组
        }
        else {
            right.push(arr[i]);//基准点的右边的数传到右边数组
        }
        console.log(arr)
    }
    return quickSort(left).concat(numValue, quickSort(right));//递归不断重复比较
}
console.log(quickSort([9,8,7,6,5,4,3,2,1,0]));

效果截屏;

quick.png

堆排序

思想：由于堆是用数组模拟的。得到一个大根堆后，数组内部并不是有序的。因此需要将堆化数组有序化。思想是移除根节点，并做最大堆调整的递归运算。第一次将heap[0]与heap[n-1]交换，再对heap[0...n-2]做最大堆调整。第二次将heap[0]与heap[n-2]交换，再对heap[0...n-3]做最大堆调整。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间，故操作完后整个数组就是有序的了。
代码：

function heapSort(array) {
    function swap(array, i, j) {
        var temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

    function maxHeapify(array, index, heapSize) {
        var iMax,
            iLeft,
            iRight;
        while (true) {
            iMax = index;
            iLeft = 2 * index + 1;
            iRight = 2 * (index + 1);
            if (iLeft < heapSize && array[index] < array[iLeft]) {
                iMax = iLeft;
            }
            if (iRight < heapSize && array[iMax] < array[iRight]) {
                iMax = iRight;
            }
            if (iMax != index) {
                swap(array, iMax, index);
                index = iMax;
            } else {
                break;
            }
        }
        console.log(array)
    }

    function buildMaxHeap(array) {
        var i,
            iParent = Math.floor(array.length / 2) - 1;
        for (i = iParent; i >= 0; i--) {
            maxHeapify(array, i, array.length);
        }
    }

    function sort(array) {
        buildMaxHeap(array);
        for (var i = array.length - 1; i > 0; i--) {
            swap(array, 0, i);
            maxHeapify(array, 0, i);
        }
        return array;
    }

    return sort(array);
}
console.log(heapSort([9, 8, 7, 6, 5, 4, 3, 2, 1, 0]))

效果截屏：

heap.png

总结

sort.jpg