论文原文 Majority is not Enough: Bitcoin Mining is Vulnerable
论文的意义
给出了一种在挖矿之外, 可以获得更大收益的算法, 同时这个算法不利于整个网络的利益, 证明了比特币POW不是激励相容的.
一般人们认为比特币的POW是激励相容的(incentive-compatible), 即大家都单纯地追求自己的利益最大化, 按照这种方式去做, 同时能够达到全局的最优结果 (安全性高, TPS高等).
激励相容
在市场经济中,每个理性经济人都会有自利的一面,其个人行为会按自利的规则行为行动;如果能有一种制度安排,使行为人追求个人利益的行为,正好与企业实现集体价值最大化的目标相吻合,这一制度安排,就是“激励相容”
这篇文章中提出的算法, 私自矿池挖出新块之后, 暂时不发布这个区块, 而是继续挖下一区块, 当发现网络上别人也挖出新区块时再发布这个区块, 可以获得更高的收益.
同时这个更高收益的算法并不是全局最优的, 因为矿工会为了更高的利益进行自私挖矿, 使得自私矿池越来越大, 逐渐变成多数, 破坏了比特币的去中心化.
虽然在自私挖矿攻击中, 诚实和自私矿池都会浪费算力, 但是诚实矿池浪费的算力会更多, 同时自私矿池可以获得比自己诚实挖矿更高的收益. 此消彼长, 矿工会更愿意加入自私挖矿.
而且, 自私矿池的算力越大, 它能够获得的奖励高于线性增长. 这更加有利于自私矿池吸引更多矿工加入.
过程
自私矿池挖到块A之后不直接发布全网, 只在自己的矿池中广播该块, 形成私有链, 并且继续挖下一块B
-
当检测到网络上有人发出下一块A'时, 再广播自己挖到的块, 使网络进入竞争状态.
如果自私矿池挖出B时, 直接发布, 让全网转到自己的链上, 自己获得块A和块B的收益, 同时浪费掉了网络在A'以及分叉上使用的算力.
如果诚实节点在块A后挖出了新块, 那么自私矿池享受块A的利益.
如果诚实节点在块A'后挖出新块, 那么自私矿池不获利.
分析
γ代表诚实节点选择在自私矿池发布的区块上挖矿的比例, (1-γ)则是诚实节点在竞争区块上挖矿的比例.
α是自私矿池的算力大小, (1-α)是诚实节点的算力总和.
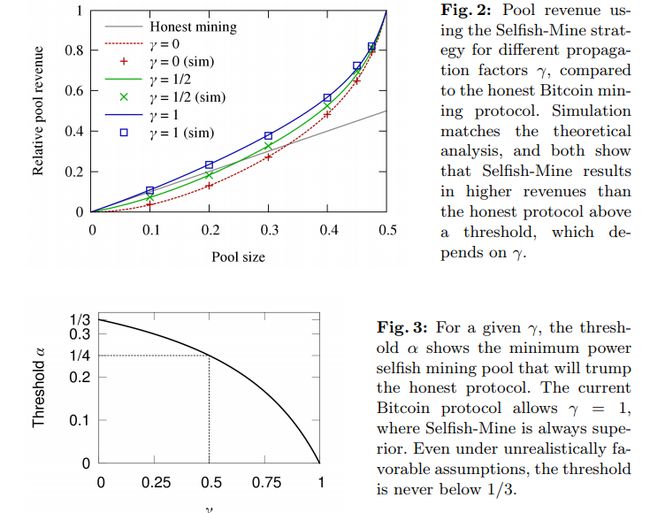
第一张图可以看到, 无论自私矿池的私有块在竞争中能否胜出, 在自私矿池的算力高于一定比例时, 都能获得超过诚实挖矿的收益.
第二张图可以看到:
当γ为1时, 无论自私矿池算力多少都可以获得更大收益
当γ为1/2时, 自私矿池算力超过全局的1/4即可获得更大收益
当γ为0时, 自私矿池算力超过全局1/3即可获得更大收益.
改进方法
比特币规定矿工在收到的第一个高度最高的新块基础上挖矿. 那么, 如果自私矿池的网络条件极好, 是有可能让其他矿工更早地收到自己的私有块, 让γ趋近于1的 (或者说比特币的POW允许γ=1出现), 此时α趋近0, 自私矿池无论算力多少, 一定获得更高收益.
一个改进方式是, 矿工收到两个竞争区块的时候, 随机抽取其中一个进行挖矿, 这样γ平均为1/2, α也就在1/4左右, 即自私矿池至少掌握1/4算力才可以获得更大收益.