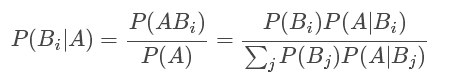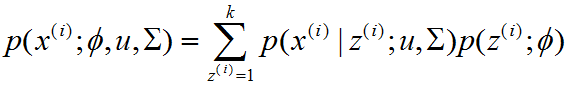一、全概率公式与贝叶斯公式
这两个公式是十分十分重要的公式,在概率统计中用的非常多。这里的EM思想,也是用到了 这两个公式的思想。关于这两个公式,这篇博客讲的很细致 理解全概率公式和贝叶斯公式
1.1 、全概率公式
1.1.1 、从网页中完备事件组看起,一直到“村里有东西被偷”的概率,这个用到了全概率公式。
直接求“村里被偷的概率”不好求,而小偷活动的概率,活动以后得手的概率已经知道,所以可以由上面这些,推出结果
但是,这个例子确实用了全概率公式,但是 ,假设的前提并不准确:
按照上述,完备事件组中的Bi就是,小偷A偷了东西,小偷B偷了东西,小偷C偷了东西,这三个事件两两互斥,在这里没体现出来。
1.2、贝叶斯公式
在全概率公式中,如果将A看成是“结果”,Bi看成是导致结果发生的诸多“原因”之一,那么全概率公式就是一个“原因推结果”的过程。但贝叶斯公式却恰恰相反。贝叶斯公式中,我们是知道结果AA已经发生了,所要做的是反过来研究造成结果发生的原因,是XX原因造成的可能性有多大,即“结果推原因”。
仍然用“小偷”这个例子 。“村子被偷”作为结果,“有人偷”作为原因。
全概率公式:因为直接求“村子被偷”不好求,所以这里把“村子被偷”作为结果,然后“有人偷”作为原因,利用全概率公式,可以求得。
贝叶斯公式:假设,现在村子已经被偷了,我想求得 是谁偷的概率
即,已知结果,求原因。可以利用贝叶斯公式。
注意:确定了“完备事件组”的前提以后,已知P(Bi)和P(A|Bi)是就可以求出全概率公式的结果以及贝叶斯公式的结果的
- 全概率公式:已知P(Bi)和P(A|Bi),求P(A)。(已知原因,求结果)
P(A)=sigma P(A|Bi)P(Bi) - 贝叶斯公式:已知P(Bi)和P(A|Bi),求P(Bi|A)。(已知结果A,求原因)
----1、先利用全概率公式求出P(A)。
P(A)=sigma P(A|Bi)P(Bi)
----2、利用贝叶斯公式求出P(Bi|A)
-------------------------------------------------------------------------------
比如,上面小偷的问题,已经知道昨天村子丢东西了,求是A偷的概率。
(典型的已知结果,求原因)。就是求P(B小偷A|A)。贝叶斯公式。
-------------------------------------------------------------------------------
带菌的问题
‘带菌率低到只有0.03,甚至比误检率还要低。这句话也挺有意思,也就是说明,可能检查10000个人,有100个误检了,50个呈阳性,但是带菌的真正有30个,所以若这个人呈阳性,是很可能被误检了的。有时候相信数字是正确的选择。
关于男女生分类的这一题,可以看出:
- 1、无论怎么分类,最后都是需要预测的
- 2、同样一个问题,有时可以用判别模型, 也可以用生成模型。
已知特征+已知特征对应的类别+已知分布(或假设出分布) ==>可以用生成模型
已知特征+已知特征对应的类别 ==> 可以用判别模型
从上面也可以看出,生成模型的条件比较苛刻,所以,一旦能用生成模型,就一定能用判别模型。(比如这个问题以及垃圾邮件分类问题,可以用朴素贝叶斯,就可以用SVM。)
- 3、当然也可以看出,对于这么小的样本,真的是用朴素贝叶斯比较好,也比较合理。更加验证了,生成模型在小样本上的表现好的优点。
-----------------------------------------------------------------————
而在机器学习中应用贝叶斯公式的时候,就不要纠结什么因果了,纠结特征是因还是果没有什么用。上面提出公式,用因果来分析,只是因为便于理解和记忆,实际上, 也就是由a推出b,那么b能推出a的关系。
也就是,在高斯混合模型中(GMM),E步,已知P(z),P(x|z),求P(z|x)。
由上面可知,直接利用贝叶斯公式就可以。不用纠结谁是因谁是果,没必要。
P(x|z)这个的意思,我们认为此时(在选定z的条件下)的x服从多值高斯分布。
二、与K-means的比较
因为突然转到概率上的参数,有点懵,所以这里准备通过让混合高斯模型和上篇文章所讲的K-means聚类联系起来,分析相同点与不同点,来分析此模型。
1、与与k-means的硬指定不同,我们首先认为隐含类别标签Z(i) 是满足一定的概率分布的。
不太可能说,1000个样例正好平均分成10类,每一类100个。所以,我们认为Z(i)不是符合均匀分布,在这里,我们认为Z(i)满足多项式分布。 (个人认为并不是满足传统的多项式分布的,因为正经的多项式分布,应该是掷骰子20次,1-6个数字出现为X=[2,4,5,6,0,3]的概率,这个X才是随机变量,有66种可能。)
这里可能是类似于讲义上的写的笔记的种类分布,而Z(i)=j 意味着Z向量的第j个数为1,其余的zi都为0 。于是,Z向量也只能有K个值,每个值对应着一个类的概率Φ。于是可以近似的写成Z(i)=j 。。。先这么理解着吧。2、因为这里的类别标签Z(i)是用概率表示的,所以,没法用K-means一样的方法去判别样例x^(i)距离那个类的质心的坐标最近。
这里通过概率联系起来,因为都是概率,所以可以在后面用极大似然估计,联系起来。这里我们认为x(i)服从多值高斯分布(n个特征,每个特征服从一个高斯分布)。
而判断样例x(i)属于哪一个类,通过后验概率计算出p(zi|xi)的值,可以认为,属于概率大的zi的那一类。
注意:
- 3、混合高斯模型不同于K-means的硬指定:在每次循环中指定每个样例属于某个类别(距离最小的那个质心)。
混合高斯模型属于软指定。即:除了最最开始的时候,(这一点倒类似于k-means一开始的时候),先随机为每个样例指定其属于哪个类别z(i)
在利用上面随机指定(已知类别, 利用有监督学习,用极大似然估计函数),求得三个参数 以后 ,在E步中,计算出每个样例xi属于每个类别zj的概率wj。并不强硬地说,xi属于概率最大的这一类,而是保留起来这些概率。留着在M步中,利用这些概率wj来计算出新的三个参数,如此循环下去。
类似于K-means中M步求每一类的质心的方法:面对每一个类,对属于这一类的所有样例的坐标求平均。即,共有100个样例,2个类。此时E步得到的第2类共有30个,M步中第二类的质心就是这三十个坐标相加再除以30.
混合高斯模型因为是采用了软指定,所以在E步中,每个样例都有对应的k个类。所以相比于K-means,计算量是它的K倍。伪代码如下:
for step to 收敛:
E步:
for j in range(k):
for i in range(m):
计算每个样例属于第j类的概率。
M步:
for j in range(k):
phi_j = 所有的(样例属于第j类的概率的)平均值
miu_j = 所有的(样例属于第j类的概率 * 该样例的特征向量)/所有的(样例属于第j类的概率)
sigma 同理
三、混合高斯模型(使用期望最大化(EM)算法来进行密度估计)
给定训练样本
隐含类别标签用z(i)表示,不同于K-means的硬指定,我们认为z(i)是满足一定的概率分布的(多项式分布)。
并且,我们认为在给定z(i)后,样例x(i)满足多值高斯分布,即:
由此可以得到联合分布:
联合分布,是为了在最开始的时候,指定每个样例所属类别以后,利用有监督学习的算法,利用极大似然估计方法估计参数。从而开始真正的EM。
-----------------------------------------------------------------------------------------------------
整个模型,可以描述为,对于每个样例x(i),是我们先从k个类别中按照多项式分布采样得到一个z(i),在确定了z(i)以后的条件下,按照多值高斯分布(每个特征都符合一个高斯分布)采样得到一个样例x(i)。因为有k个类别,所以相当于全概率公式中,把样本空间S分成了k个,所以需要k个相加,对应到p(x)的概率分布上就是
-----------------------------------------------------------------------------------------------
按照极大似然估计的思想,已知数据只有样例m个x(i),且符合一定分布,最极端理想的情况就是,参数就是正好出现m个样例x(i)的情况,联合分布的概率是1。
极大似然就是最大化这个联合分布,用来估计x(i)服从的分布参数。
对数化后如下:
这个式子的最大值是不能通过前面使用的求导数为0的方法解决的,因为求的结果不是close form。但是**假设我们知道了每个样例的类别标签z(i),那么上式可以简化为:
--------------------------------------------------------------------------------------------
注意,这一点也体现了EM算法的思想:开始可以凑合着过,反正后面的日子会越来越好。
解释:比如,K-means中一开始,就先随机指定了质心坐标。
这里 也是,因为对数化后的极大似然公式仍然难求,
- 最开始:
指定类别概率(或质心坐标):先随机给每个样例随机指定类别,这样初步算是有监督学习 - 再然后估计出稍微好点的参数:
此时类别已经确定,可以利用有监督学习的方法求导等于零得到分布的三个参数,总归是比不知道或者瞎蒙强啊 - E步(期望达到目标,得到最好的分类):
已经得到了稍微好点的参数:利用已经得到的参数再去计算类别概率(或者类别质心)。 - M步(根据分好的类,最大化似然函数,估计出参数):
已经得到类别,利用极大似然估计方法, 估计出参数。 - 循环EM步直至收敛。
--------------------------------------------------------------------------------------------
接着上面公式讲:
当知道z(i)后,最大似然个估计就类似于高斯判别模型了。所不同的是GDA中类别y是伯努利分布,而这里的z是多项式分布,还有这里的每个样例都有不同的协方差矩阵,而GDA中认为只有一个。
这时候再对三个参数进行求导,得到:
之前已经讲的很清楚了,EM思想,这里应用到GMM中,就是先随意 给每个样例猜测一个类别z(i),然后再用上面公式计算(有监督了)三个参数。然后就是,
期望达到目标(得到更好的类别的质心或概率分布)
最大化似然函数得到更好的参数估计
这里我们发现, 用Wj(i)代替了前面的φi,由前面简单的0/1值变成了概率。
这是因为,不同于GDA中每个样例对应的标签zi是确定的。这里除了最开始的一步,剩下的情况下,每个样例的类别zi是服从一个分布的,在对每个样例求所述类别是,都需要用贝叶斯公式才行。
E步中,已知各个参数分布,求每个样例x(i)对应的类别z(i)的概率。
即已知p(z),p(x|z),求p(z|x)(和一开始模型中,先采样z(i)以后在在此条件下采样x(i)形成对比),想到用贝叶斯公式。
Wj(i)计算公式如下:
对比K-means可以发现,这里使用了“软”指定,为每个样例分配的类别z(i)是有一定的概率的,同时计算量也变大了,每个样例i都要计算属于每一个类别j的概率。与K-means相同的是,结果仍然是局部最优解。对其他参数取不同的初始值进行多次计算不失为一种好方法。
接下来介绍一般化的EM推导过程。