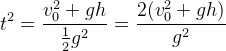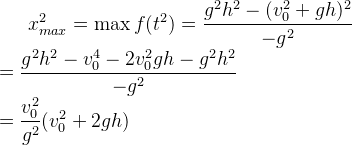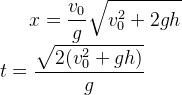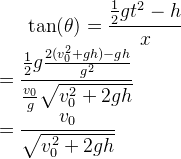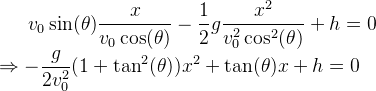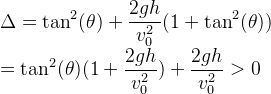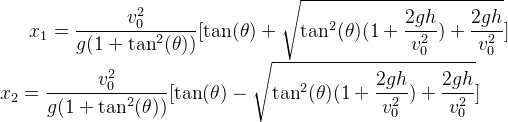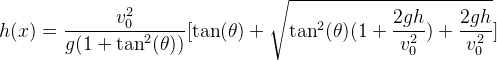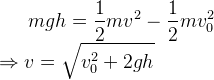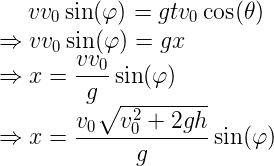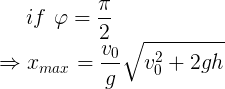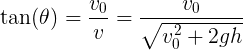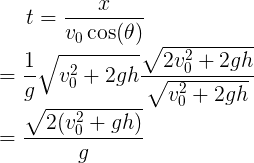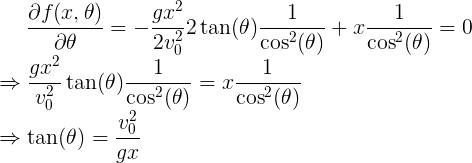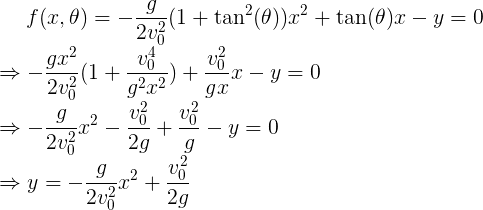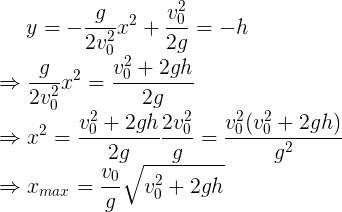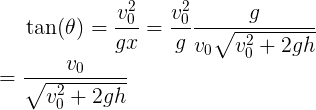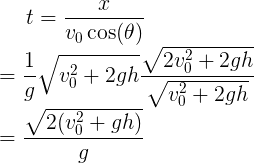本章涉及知识点
1、案例引出
2、运动过程分析
3、解法一:构造关于时间t的二次函数
4、解法二:构造关于水平位移x的二次函数
5、解法三:分析矢量速度三角形面积
6、解法四:包络线方程
7、带入数据测试4种不同解法的正确性
8、心得总结
一、案例引出
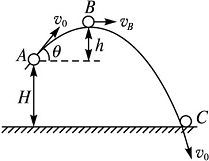
在高度为h,以初速度v0和任意角度斜抛出一个物体,求解:该物体可以运动到的最远水平距离x和运动时间t?以及使物体运动到最远采取的斜抛角度θ的策略?(忽略空气阻力)
二、运动过程分析
分析物体运动的水平和竖直方向,由于物体在水平方向不受外力作用,而在竖直方向只受重力作用,即
则我们可以写出物体在任意时刻t的水平和竖直位移,即
上述方程组包含未知量为:角度θ、时间t、水平位移x和竖直位移y,下面我们就需要推导这组方程组
三、解法一:构造关于时间t的二次函数
这个解法是容易可以想到的,我们来首先计算出时间t,则需要消去角度θ
我们将方程组进行分离变量t和θ,并带入y=-h,即得到
由于要消元θ,将方程组两边平方得到
相加两个方程,得到
可以看到消元θ后,我们得到关于x和t的一个方程,分离变量得到
上述方程包含x和t,我们构造x^2关于t^2的二次函数f(t^2),即
我们要求出x的最大值,即求f(t^2)的最大值,则f(t^2)的对称轴为
f(t^2)的最大值在对称轴上取得,即
此时我们利用二次函数求出了t和x,即
下面我们来推导使得x到达最远的角度θ策略,我们回到初始方程组
相除两个方程,并带入求出的x和t,可化简得到
则我们得到使得x取得最大值的角度θ为
四、解法二:构造关于水平位移x的二次函数
解法二和解法一思路是一样的,同样是利用下面方程组来推导
不同的是,我们选择消去时间t来计算角度θ,则由第一个方程得
带入第二个方程消去t,并带入y=-h,得到
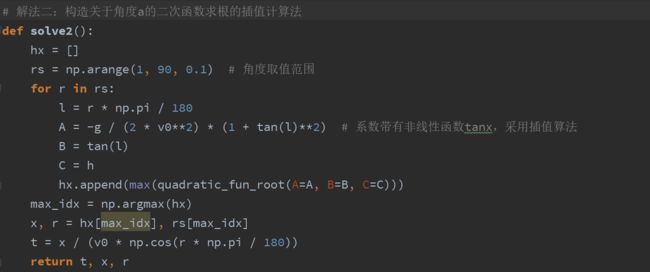
上述方程包含tanθ和x两个变量,我们将方程视为关于x的二次方程,即
此时特别注意:比较解法一,我们无法利用二次函数的对称轴来求解x的最值,因为这个二次函数的系数不是单变量θ,而是非线性函数tanθ!
故我们先求出根的判别式
可以看到,该二次函数f(x)一定有两个实数解,利用求根公式,得到f(x)的解为
我们令
则我们要求x的最大值,即转化求h(x)的最大值,而h(x)不是初等函数,故需要对h(x)求一阶导数
但是推导到这里,我们发现h(x)的表达式包含分式、非线性函数和开根号等复合函数,导致其导数将非常难求,故我们无法利用数学来推导h(x)的极值
为此,我们只能采取数值计算的方法,通过编程来插值计算h(x)
五、解法三:分析矢量速度三角形面积
上述解法都是从位移方程组出发来消元的,我们重新换一种思路,因为整个运动过程只有重力做功,我们设运动结束的速度为v,列出动能方程,即
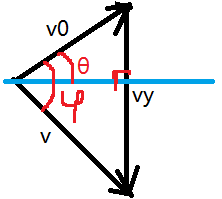
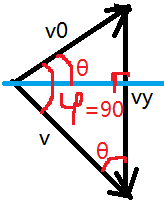
至此,我们发现落地速度v是一个常量,分析运动结束的速度矢量三角形,有如下三个分量
可以看到落地速度v(在运动的切线方向)和初速度v0都是常量,只有竖直方向的速度vy是一个变量
我们引入新的变量φ表示:v和v0之间的夹角
则我们用v、v0和φ列出该三角形的面积为
我们在找出该三角形面积的另一个表达式,用vy和vy边上的高即可
至此,三角形面积是相等的,我们将两个面积表达式写在一起,即
我们根据面积的不同表达式得到上述方程,发现含有φ、θ和t三个变量,我们需要消元
由水平位移方程
可以看到整个x的表达式出现在上述方程的右侧,带入得到
至此,我们得到x的关系表达式,且x的大小和正比于变量sin(φ),而sin(φ)最大值为1,即当
至此我们求出当φ为90度的时候,x取得的最大值,则由几何知识可以得到v和vy的夹角也为θ
从上图几何关系中,我们可以直接求出θ,即
即可以求出使得x取得最大值的夹角θ为
我们求出了x和θ,直接带入水平位移方程,即可求出t,即
可以看到解法三求出的关于x、t和θ的数学表达式和解法一是一样的
六、解法四:包络线方程
我们考虑更一般的情景,还是从水平位移和竖直位移的方程组出发
和解法二类似,我们联立上述方程组消去时间t,得到
特别注意,此时我们并没有带入y=-h这个条件,而是将y也当做变量(准确来说是某个函数表达式)
至此,回顾解法二,我们是将上述方程视为关于x的二次方程,但是发现解不出来其一阶导数,故解法二采用数值计算来分析,所以我们需要从数学的角度,重新换一个角度来审视上述方程
所以我们定义
我们构造的函数f(x, θ)有如下数学意义和物理意义:
(1)f(x, θ)的数学意义为:以x和θ为自变量,且包含关于θ隐函数
(2)f(x, θ)的几何物理意义为:表示物体以任意角度做抛物线运动的轨迹方程
由于θ和任意一个抛物线运动都是一一对应的,即θ是抛物线运动轨迹的特征参数,θ是单值的,则在数学上可以翻译为:轨迹函数f(x, θ)对θ的偏导数为0
我们带入f(x, θ)求出θ的偏导数,即
至此我们得到θ和x的关系式,我们将tanθ带入f(x, θ),化简得到
可以看到,我们推导出了y的函数表达式,且y是以x为单自变量的开口向下的二次函数,数学上我们将y称为:包络线方程
包络线的几何意义为:
(1)包络线是一条光滑连续的曲线
(2)包络线保证同一类运动的轨迹方程(抛物线族)有且和包络线曲线相切有一个交点
(3)同一类抛物线族都在包络线的范围之内
至此,我们令包络线y=-h,即可解出x的最大值,即
将x的表达式带入tanθ,即
即可求出θ
求出x和θ后,带入水平位移方程,即可求出t
可以看到解法四求出的关于x、t和θ的数学表达式和解法一、解法三是一样的
七、带入数据测试4种不同解法的正确性
我们以投掷实心球的场景,假设出手初速度v0=10m/s,身高h=1.7m,重力加速度g=9.78m/s^2
通过python编程实现上述四种解法,得到的结果如下
可以看到无论哪种算法,计算的结果都是一样的,只是思考方向和角度不同
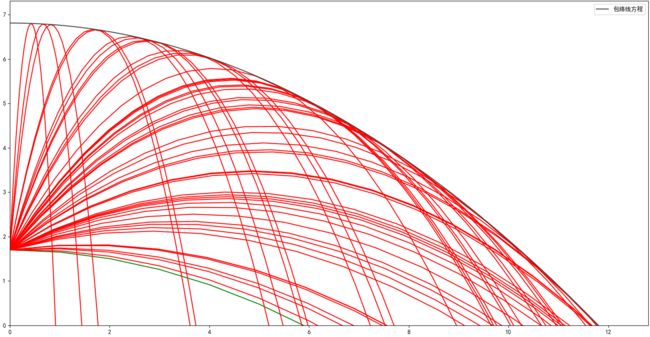
最后,我们在上述场景里可视化画出解法四的包络线方程和抛物线族
可以看到,物体无论以什么角度做斜抛运动,其抛物线运动轨迹(红色)均在包络线方程范围内
8、心得总结
(1)解法一最直接,却要注意消元的选择,保证推导的函数没有包含复合函数,计算量中等
(2)解法二由于带有复合函数,导致求导异常困难,适用数值计算方法,计算量太大
(3)解法三需要一定的技巧和观察能力,计算量最小,高效却不灵活
(4)解法四需要用另一个角度去审视轨迹方程,模型最通用,计算量中等
案例代码见:斜抛运动的数学模型