数据结构(5)-哈夫曼树和平衡二叉树(AVL树)

哈夫曼树

概念

考虑不同节点的权值，权值大的节点距离根节点近，权值小的节点距离根节点远。让所有节点的访问次数的距离最小的二叉树，就是哈夫曼树。

带权路径长度

树的带权路径长度指树中所有叶子节点到根节点的路径长度与该叶子节点权值的乘积之和，如果在一棵二叉树中共有n个叶子节点，用Wi表示第i个叶子节点的权值，Li表示第i个也叶子节点到根节点的路径长度，则该二叉树的带权路径长度

WPL=W1*L1 + W2*L2 + ... Wn*Ln。

哈夫曼树的特性

1. 对于同一组权值，所能得到的赫夫曼树不一定是唯一的。
2. 赫夫曼树的左右子树可以互换，因为这并不影响树的带权路径长度。
3. 带权值的节点都是叶子节点，不带权值的节点都是某棵子二叉树的根节点。
4. 权值越大的节点越靠近赫夫曼树的根节点，权值越小的节点越远离赫夫曼树的根节点。
5. 赫夫曼树中只有叶子节点和度为2的节点，没有度为1的节点。
6. 一棵有n个叶子节点的赫夫曼树共有2n-1个节点。

哈夫曼树的构造

赫夫曼树的构建步骤如下：

1. 将给定的n个权值看做n棵只有根节点（无左右孩子）的二叉树，组成一个集合HT，每棵树的权值为该节点的权值。
2. 从集合HT中选出2棵权值最小的二叉树，组成一棵新的二叉树，其权值为这2棵二叉树的权值之和。
3. 将步骤2中选出的2棵二叉树从集合HT中删去，同时将步骤2中新得到的二叉树加入到集合HT中。
4. 重复步骤2和步骤3，直到集合HT中只含一棵树，这棵树便是赫夫曼树。

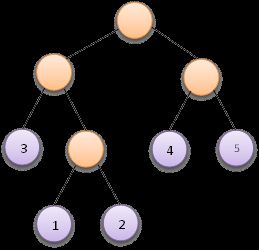
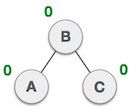
假如给定如下5个权值：

则按照以上步骤，可以构造出如下面左图所示的赫夫曼树，当然也可能构造出如下面右图所示的赫夫曼树，这并不是唯一的

平衡二叉树(AVL树)

定义

一个树的左子树和右子树的深度相差绝对值不超过1，那么就是一个平衡二叉树。

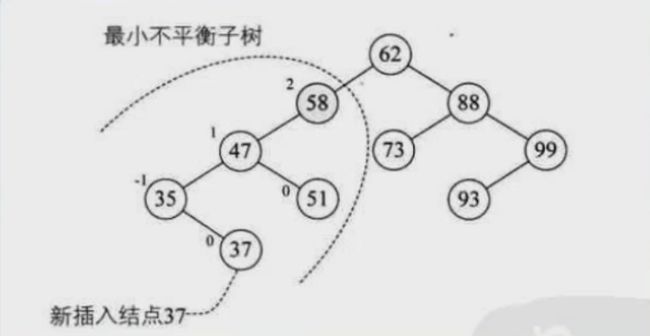
最小不平衡子树

距离插入结点最近的，而且平衡因子的绝对值大于1的结点为根的子树，称为最小不平衡子树。

构建AVL树(平衡二叉树)

构建平衡二叉树时，会出现一个树失衡的情况，那么当一个树从平衡二叉树转变成不平衡二叉树时，需要进行处理。处理方式包括左旋和右旋。

AVL树中的结点的数据结构可以表示为:

/**
 * Created by apple on 16/7/30.
 */
public class AVLNode {

    //节点的值
    public int key;

    //节点的平衡度
    public int balance;

    //分别指向节点的左孩子、右孩子与父节点
    public AVLNode left, right, parent;

    /**
     * @function 默认构造函数
     * @param k
     * @param p
     */
    AVLNode(int k, AVLNode p) {
        key = k;
        parent = p;
    }
}

Rebalance:平衡调整

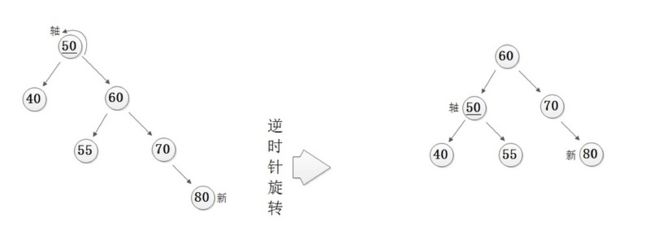
AVL树的调整过程很类似于数学归纳法，每次在插入新节点之后都会找到离新插入节点最近的非平衡叶节点，然后对其进行旋转操作以使得树中的每个节点都处于平衡状态。

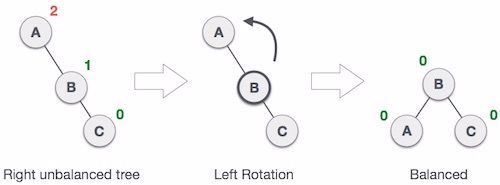
Left Rotation:左旋,右子树右子节点

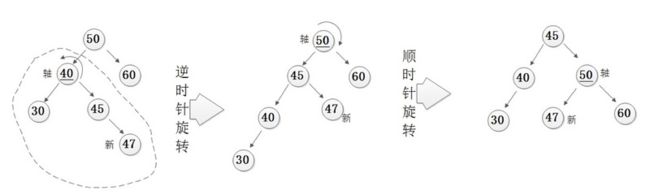
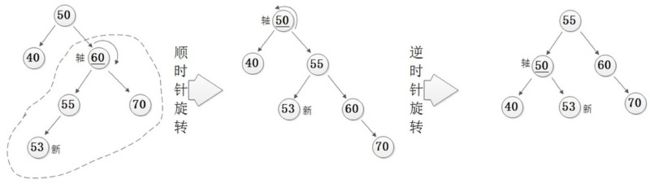
当新插入的结点为右子树的右子结点时，我们需要进行左旋操作来保证此部分子树继续处于平衡状态。(左下右上)

复杂一点的情况

如果要上去的有左结点，那么这个左结点放在要下来的右结点的右边

/**
 * @param a
 * @return
 * @function 左旋操作
 */
private AVLNode rotateLeft(AVLNode a) {

    //指向当前节点的右孩子
    AVLNode b = a.right;

    //将当前节点的右孩子挂载到当前节点的父节点
    b.parent = a.parent;

    //将原本节点的右孩子挂载到新节点的左孩子
    a.right = b.left;

    if (a.right != null)
        a.right.parent = a;

    //将原本节点挂载到新节点的左孩子上
    b.left = a;

    //将原本节点的父节点设置为新节点
    a.parent = b;

    //如果当前节点的父节点不为空
    if (b.parent != null) {
        if (b.parent.right == a) {
            b.parent.right = b;
        } else {
            b.parent.left = b;
        }
    }

    //重新计算每个节点的平衡度
    setBalance(a, b);

    return b;
}

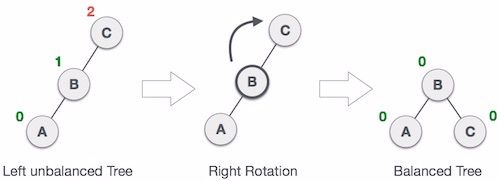
Right Rotation:右旋,左子树左子节点

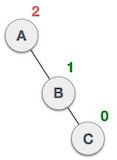
当新插入的结点为左子树的左子结点时，我们需要进行右旋操作来保证此部分子树继续处于平衡状态。(右下左上)

复杂的情况

如果要上去的结点有右结点，那么这个右结点就放在要下来的结点的左边

private AVLNode rotateRight(AVLNode a) {

    AVLNode b = a.left;
    b.parent = a.parent;

    a.left = b.right;

    if (a.left != null)
        a.left.parent = a;

    b.right = a;
    a.parent = b;

    if (b.parent != null) {
        if (b.parent.right == a) {
            b.parent.right = b;
        } else {
            b.parent.left = b;
        }
    }

    setBalance(a, b);

    return b;
}

Left-Right Rotation:先左旋再右旋,左子树右子节点

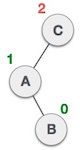
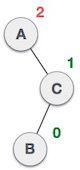
在某些情况下我们需要进行两次旋转操作，譬如在如下的情况下，某个结点被插入到了左子树的右子结点：(这种情况下，需要旋转结点的根结点的父结点和子结点都比它大)

1. 原始树

   
   
   

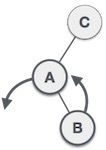
2. 首先要以A为轴进行左旋操作

   
   
   

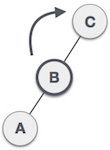
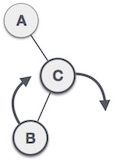
3. 然后需要以C为轴进行右旋操作

   
   
   

4. 最终得到的又是一棵平衡树

   
   
   

复杂情况

private AVLNode rotateLeftThenRight(AVLNode n) {
    n.left = rotateLeft(n.left);
    return rotateRight(n);
}

Right-Left Rotation:先右旋再左旋,右子树左子节点

1. 原始的树

   
   
   

2. 先右旋

   
   
   

3. 再左旋

   
   
   

4. 结果

   
   
   

复杂情况

private AVLNode rotateRightThenLeft(AVLNode n) {
    n.right = rotateRight(n.right);
    return rotateLeft(n);
}

数据结构导读目录