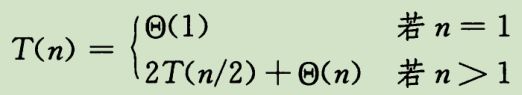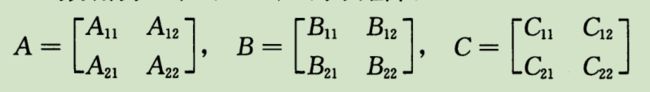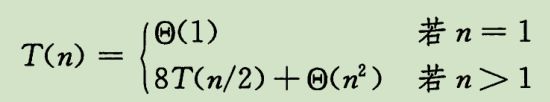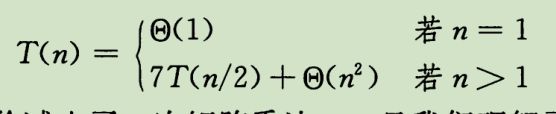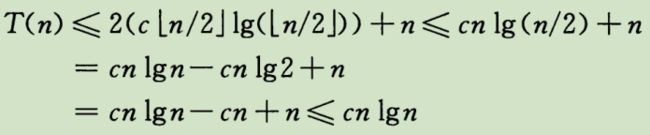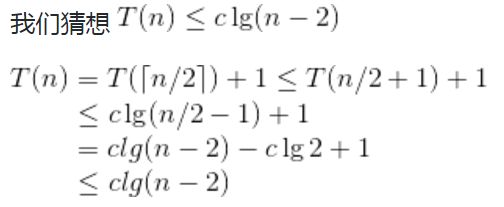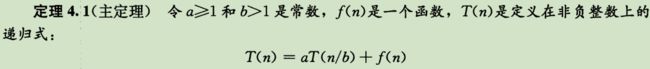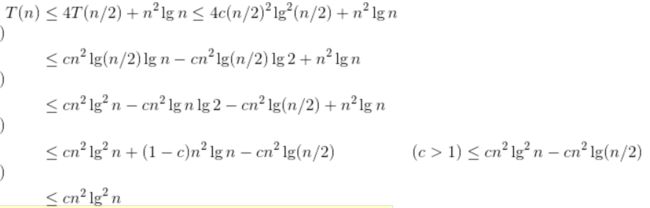本章介绍分治法，首先通过前两节最大子数组、矩阵乘法两个问题说明分治法的一般步骤：分解，解决，合并。当子问题需要递归求解时称为递归情况，足够小可直接得出解为基本情况，其余一些与原问题不同子问题看做合并步骤部分。
然后介绍三种递归式的解法：代入法、递归树法和主方法。

代入法：猜测算法的复杂度界，用数学归纳法证明正确性。
递归树法：将递归式转换为树，结点表示不同层次的递归调用产生的代价。然后采用边界和技术求解。
主方法：求解如下递归式的界

一般忽略递归式声明、求解的技术细节和向下、向上取整及边界条件。

4.1 最大子数组问题

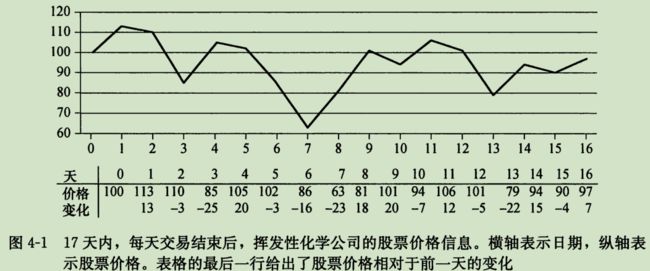
问题描述：一个记录每天股票价格的数组，寻找一段日期，使得从第一天到最后一天股票价格净变值最大。

分析：第一个想法：最低价格买进，最高价格卖出时收益最大，但是最高价可能比在最低价更早出现。那么最低价格买进或者最高价格卖出呢？即：

寻找最高和最低价格
从最高价开始向左寻找之前的最低价；从最低价开始向右寻找之前的最高价。
取两对价格中差值最大者。

有反例：

说明有时最大收益既不是在最低价时买进，也不是最高价卖出。

暴力法：尝试每对可能的买进、卖出的日期组合，Ω(n^2)的复杂度。

问题变换

不从每日价格的角度看待输入，而是考察每日价格变化，即当天和前一天的价格差。原输入数组变为：

那么问题转化为 寻找A的和最大的非空连续子数组——最大子数组。

使用分治法求解

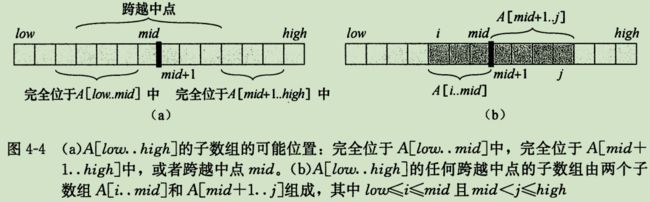
首先将原问题分解为一些规模相近的子问题，即将原数组分两半分别求解。A 的任何连续子数组的位置必然是以下情况：

故可以递归求解前两个，然后寻找跨中点的最大子数组，最后三者中取最大。

找跨中点的最大子数组可在线性时间内完成：找出A[i ... mid] 和 A[mid + 1 ... j]的最大子数组然后合并。与原问题不同在于： 此子数组必须包含A[mid]。
伪代码：

所以最大子数组问题分治算法伪代码为：

C++实现：

int a[20] = {0, 13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7};
struct node
{
    int mxl, mxr, sum;
};
node CrossSum(int a[], int low, int mid, int high)
{
    int i, j, sum, maxl, maxr;
    int leftsum = -INF;
    sum = 0;
    for (i = mid; i >= low; i --)//从中间向前遍历，故一定选中a[mid]
    {
        sum += a[i];
        if(sum > leftsum)
        {
            leftsum = sum;
            maxl = i;
        }
    }
    int rightsum = -INF;
    sum = 0;
    for (j = mid + 1; j <= high; j ++)//从中间向后遍历
    {
        sum += a[j];
        if(sum > rightsum)
        {
            rightsum = sum;
            maxr = j;
        }
    }
    node x;
    x.sum = leftsum + rightsum;   //左右最大值之和
    x.mxl = maxl;
    x.mxr = maxr;
    //printf("insub %d %d %d\n", x.mxl, x.mxr, x.sum);
    return x;
}
node FindMaxSub(int a[], int low, int high)
{
    node x, y, z;
    int i , j, mid;
    if (low == high)
    {
        x.mxl = low;
        x.mxr = high;
        x.sum = a[low];
        return x;
    }
    mid = (low + high) / 2;
    //printf("mid = %d\n", mid);
    x = FindMaxSub(a, low, mid);
    y = FindMaxSub(a, mid + 1, high);
    z = CrossSum(a, low, mid, high);
    //printf("l = %d %d %d\n", x.mxl, x.mxr, x.sum);
    //printf("r = %d %d %d\n", y.mxl, y.mxr, y.sum);
    //printf("cro = %d %d %d\n", z.mxl, z.mxr, z.sum);
    if (x.sum >= y.sum && x.sum >= z.sum)
        return x;
    else if (y.sum >= x.sum && y.sum >= z.sum)
        return y;
    else if (z.sum >= y.sum && z.sum >= x.sum)
        return z;
}

分治算法的分析

建立以上算法的递归式。首先第一行基本情况T(1) = Θ(1)。n > 1时递归情况分两半每份T(n/2)，共2 * T(n/2)。6~11行子函数Θ(n)，其余Θ(1)。故此部分共2*T(n/2) + Θ(n)。得到递归式：

与归并排序的一样，故也为Θ(nlgn)。

练习

4.1-1

答：返回A中最大的单个元素max(A[i])

4.1-2

伪代码：

FIND-MAX-SUBARRAY(A, low, high)
  left = 0
  right = 0
  sum = -∞
  for i = low to high
      current-sum = 0
      for j = i to high
      current-sum += A[j]
      if sum < current-sum
          sum = current-sum
          left = i
          right = j
  return (left, right, sum)

4.1-3

暴力算法C++实现：

node FindMaxSub(int a[], int low, int high)
{
    int i, j, right = 0, left = 0;
    int sum = -INF;
    for (i = low; i <= high; i ++)
    {
        int curs = 0;
        for ( j = i; j <= high; j++)
        {
            curs += a[j];
            if (sum < curs)
            {
                sum = curs;
                left = i;
                right = j;
            }
        }
    }
    node x;
    x.sum = sum;
    x.mxl = left;
    x.mxr = right;
    return x;
}

暴力法 T(n) = a * n^2, 递归法 R(n) = b * nlgn，比较可得交叉点。改后不会变，相当于合并图像时取两段较低的部分。

4.1-4

答：每次返回子数组之前判断和是否小于0，若是则返回sum = 0。

4.1-5

答：用动态规划的思想实现。若当前和小于0则置0重新计算。C++代码：

node FindMaxSub(int a[], int low, int high)
{
    int i, j, right = 0, left = 0;
    int sum = -INF, curs = 0;
    for (i = low; i <= high; i ++)
    {
        curs += a[i];
        if (curs > sum)
        {
            sum = curs;
            right = i;
        }
        if (curs < 0)
        {
            curs = 0;
            left = i + 1;
        }
    }
    node x;
    x.sum = sum;
    x.mxl = left;
    x.mxr = right;
    return x;
}