马拉车算法, 线性找最长回文 必考题

http://www.cnblogs.com/grandyang/p/4475985.html

http://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-1/

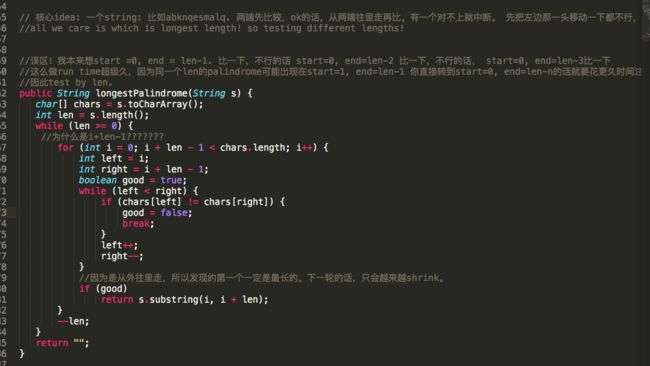
我本来的做法是 双指针两头往内比较的做法。

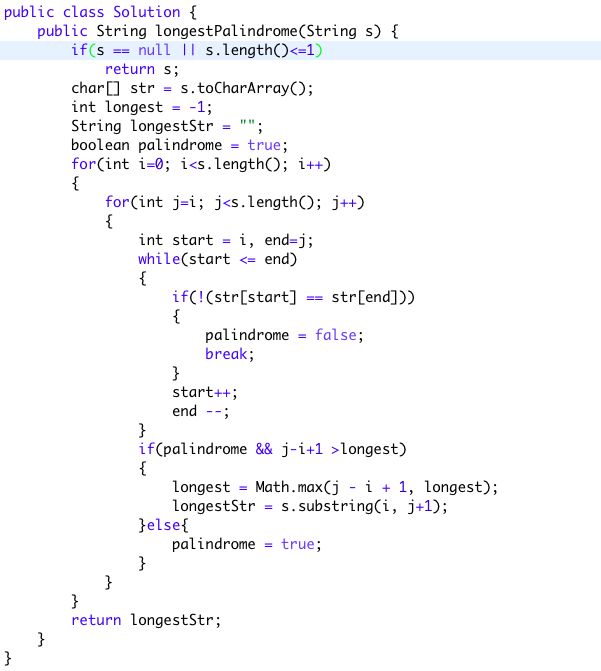
Naive Way O(n^3)

Better: O(n^2) + O(n^2) space

Better: O(n^2) time, O(1) time complexity.

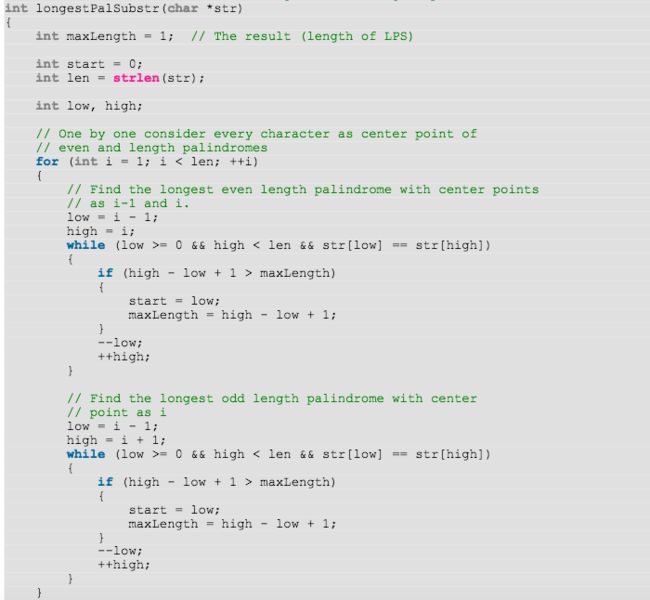
Best: O(n) 

用了之前Better的一点idea在这里。 那就是找出各个center point， 然后求左右最长相等的String.

比如abcba  c是center， 左右的的第一个字母一样， 左右的第二个字母一样。

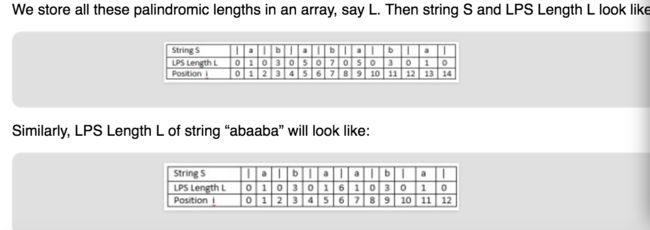
首先我们需要预处理一下整个String，每个character左右都加上一个dummy character. 这样总长度一定是odd。

最后iterate一遍这个LPS table, 最长的那个就是Longest Palindrome. 

这个算法真心非常复杂：

核心思想：

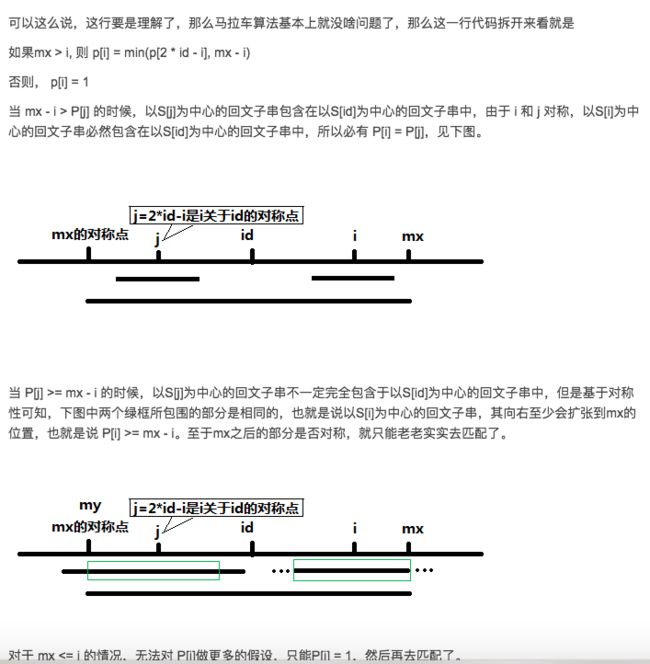
用我自己的话说就是，首先id 是一个回文的center。 左边mx和右边mx中间的字符都是对称的。

j的回文左右方向长度=p[j].  这里要注意：p[j]不是palindrome of j. 只是左右方向各半边的长度

j和i是对应的position。 如果mx-i> p[j] 就代表j距离S[id]能包住的范围距离 大于了 左边回文长度的大小。

因为在s[id]包住的范围内一切都是回文，又因为j和i在对称点。所以p[j] = p[i] if mx-i>p[j].

first character 加一个non #, last character 加一个 none #

if(i + p[i] > mx) 因为mx表示之前回文串能延伸到的最右端的位置，如果能够更远，mx = i+p[i].

id = i表示center 于i。

有几个还没有理解的地方，为什么LP = int[text.length() + 1]

为什么一开始要多加一个character, 结尾也要多加一个character, 而且两个还不能一样？

如果不这么做的话 会index out of bounds. 比如只看  "a"

preprocess => "&#a#*"

LP[] = size 6

从i = 1开始  LP[1] =0. 然后 # == #? Yes, LP[1] = 1; $ == *? NO，结束。 如果这俩一样的话, LP[i] 会变成2

下一轮就index out of bounds.  所以#是为了一种default Palindrome长度，字母自己跟自己肯定回文=1.

前后加两个是为了不让它越界，因为# 和#匹配成功后，他肯定还要再走一轮。

最下面一次iterate LP array要注意，我一开始写是取最大LP[j]的j为起始点。但是其实不对，因为我们修改过String，整个String变得非常长。起始点=(centerIndex - 1 -longest)/2 因为center的左边palidrome 那么长的地方是起始点，然后除2因为我们把string变长了一倍。