Binary Search(二分法,或者叫折半查找)
167. Two Sum II - Input array is sorted
我们来看使用二分法来解决此问题,二分法使用的前提是有序。
class Solution {
public:
int BinSearch(vector& numbers,int left, int right, int target)
{
while(left <= right)
{
int mid = left + (right - left) / 2;
if(numbers[mid] == target)
return mid;
else if(numbers[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return -1;
}
vector twoSum(vector& numbers, int target) {
for(int i = 0; i < numbers.size()-1; ++i)
{
int remainingTarget = target - numbers[i];
int left = i + 1;
int right = numbers.size() - 1;
int index2 = BinSearch(numbers, left, right,remainingTarget);
if(index2!=-1)
{
return {i+1, index2+1};
}
}
return {-1,-1};
}
};
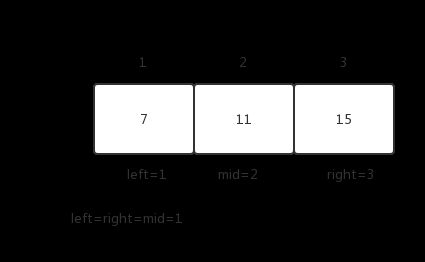
以2,7,11,15为例
(1)i = 0, remainingTarget = 9-2=7, left=1, right=3, 进入函数BinSearch
(2)在7, 11, 15中利用二分查找确认7的位置
Divide and Conquer(分而治之)
快速排序qsort是分而治之技巧的典型应用,使用前提整体解题思路与部分解题思路是一致的。
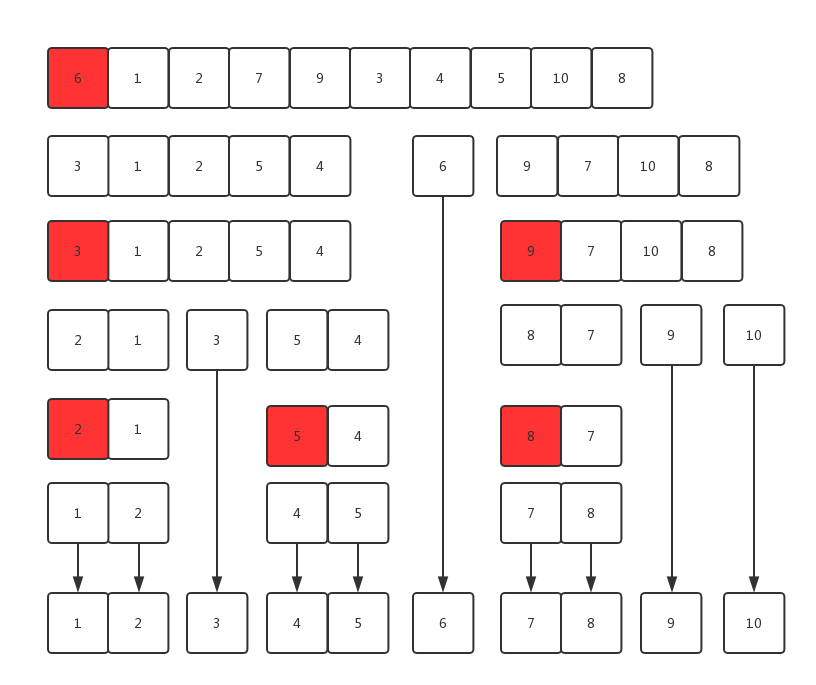
例如将6 1 2 7 9 3 4 5 10 8进行快速排序
(1)选择第一个元素(6)为基准,把小于6的元素放左边,大于6的元素放右边,即:3 1 2 5 4 6 9 7 10 8
(2)这样数组分为了两部分,3 1 2 5 4与9 7 10 8
(3)在3 1 2 5 4中,依然选第一个元素3位基准,把小于3的放左边,大于3的放右边:2 1 3 5 4
(4)我们又得到了2 1与5 4
(5)2 1以2为基准调整,变为1 2,5 4以5为基准调整,变为4 5,所以2 1 3 5 4变为了1 2 3 4 5
(6)同理 9 7 10 8经过处理变为7 8 9 10,最后得到的序列如下:1 2 3 4 5 6 9 7 10 8
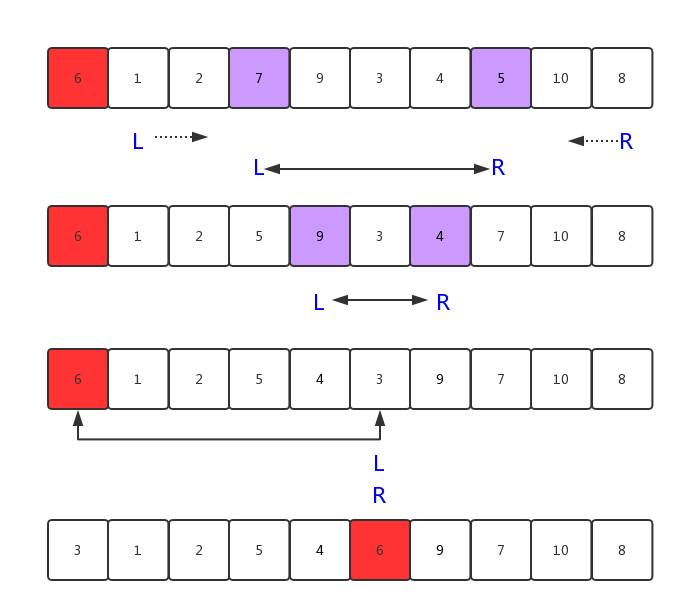
继续解释下如何把数组6 1 2 7 9 3 4 5 10 8以6为基准分成两部分(下面的partition函数操作),使得小于6的部分在左边,大于6的部分在右边。这里用到了上面的Tow Pointers(辅助指针)的技巧
(1)有L和R两个指针,分别指向第二个元素和最后一个元素
(2)L指针一直向右扫描,直到遇到第一个大于6的数字7;R指针一直向左扫描,直到遇到第一个小于6的数字5, 交换这两个数字
(3)L指针继续向右扫描,遇到大于6的数字9;R指针一直向左扫描,遇到小于6的数字4,交换这两个数字
(3)重复第二个步骤,一直到L和R指针重叠(元素3),交换基准6和重叠元素3
void Swap(int a[] ,int left,int right)
{
int tmp;
tmp=a[left];
a[left]=a[right];
a[right]=tmp;
}
int partition(int a[],int left,int right)
{
int point=a[left];
//基准点定位为第一个元素
int firstPosition = left;
while( left< right)
{
//从右往左寻找小于point的元素
while( left< right&& a[right] >= point )
right--; //移到前一个元素
//从左往右寻找大于point的元素
while( left< right&& a[left] <= point)
left++; //移到下一个元素
//交换两个元素
Swap(a,left,right);
}
//交互基准元素与最后重叠元素位置
Swap(a,firstPosition, left);
return left;
}
void QSort(int a[],int left,int right)
{
int point;//定义变量存放基准点
if( left< right)
{
point=partition(a,left,right);//对基准点定位
//对基准点左边进行递归调用
QSort(a,left,point-1);
//对基准点右边进行递归调用
QSort(a,point+1,right);
}
}
215. Kth Largest Element in an Array
寻找数组的第k大元素
给出数组[3,2,1,5,6,4] ,k = 2, return 5.
很多种技巧都可以解决上面的题目,例如暴力搜索(第一遍找到最大的,第二遍找到第二大。。。)、sort(先排序,再定位第k大)、哈希表(multiset),最大堆(priority_queue),在这里我们用分而治之思想来解决。
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int left = 0, right = nums.size() - 1;
while (true) {
int pos = partition(nums, left, right);
if (pos == k - 1) return nums[pos];
else if (pos > k - 1) right = pos - 1;
else left = pos + 1;
}
}
int partition(vector& nums, int left, int right) {
int pivot = nums[left], l = left + 1, r = right;
while (l <= r) {
if (nums[l] < pivot && nums[r] > pivot) {
swap(nums[l++], nums[r--]);
}
if (nums[l] >= pivot) ++l;
if (nums[r] <= pivot) --r;
}
swap(nums[left], nums[r]);
return r;
}
};
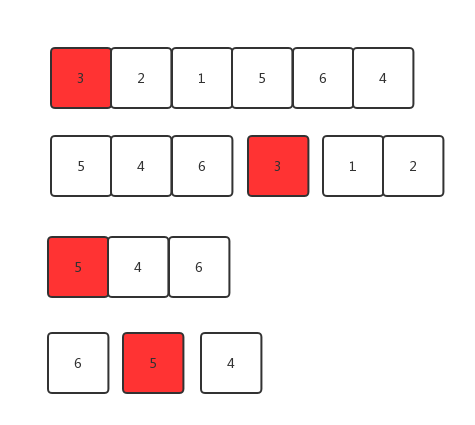
从上面qsort中的partition函数我们可以受到启发,每次partition完后比基准数小的都放右边边,比基准数大的都放在左边,如果基准数整好在(k-1)下标上,则基准数就是第k大数。如果不在,则利用返回的下标帮我们缩小查找范围。下面以3,2,1,5,6,4为例说明:
(1)第一次以3为基准,大于3的放左边,小于3的放右边,partition完后3的下标是3,大于(k-1=1),第二大元素肯定位于左边。
(2)第二次以5为基准,大于5的放左边,小于5的放右边,partition完后5的下标是1,等于(k-1=1)
怎样应对IT面试与笔试-(一)
怎样应对IT面试与笔试-(二)
怎样应对IT面试与笔试-(三)
怎样应对IT面试与笔试-(四)
怎样应对IT面试与笔试-(五)
怎样应对IT面试与笔试-(五-1)
怎样应对IT面试与笔试-(六)
怎样应对IT面试与笔试-(七)
怎样应对IT面试与笔试-(八)
怎样应对IT面试与笔试-(九)
怎样应对IT面试与笔试-(十)
怎样应对IT面试与笔试-(十一)
怎样应对IT面试与笔试-(十二)
怎样应对IT面试与笔试-(十三)
怎样应对IT面试与笔试-(十四)
怎样应对IT面试与笔试-(十五)
怎样应对IT面试与笔试-(十六)