快速排序（Quicksort）是对冒泡排序的一种改进。
它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
文字理解有些困难，先从网上找下代码看一看
public static void quickSort(int[] a, int left, int right) {
if (left >= right)
return;
int pivot = a[left];//定义基准值为数组第一个数
int i = left;
int j = right;
while (i < j) {
while (pivot <= a[j] && i < j)//从右往左找比基准值小的数
{
j--;
}
while (pivot >= a[i] && i < j)//从左往右找比基准值大的数
{
i++;
}
if (i < j) //如果i以数组第一个数值作为基值，从右向左寻找比基值小的数，从左向右寻找比基值大的数，然后互换。用i和j记录数组下标，一直到 i>=j 时，把基值和分界线值交换，把基值两边的数值继续进行快速遍历，一直到每次的快速排序左下标 > 右下标为止
大概的流程清楚点了，再加一下log准备跑一下看看
public void quickSortTest(int[] a, int left, int right) {
System.out.println("初始数组" + Arrays.toString(a) + "左边起始下标" + left + "右边起始下标" + right);
if (left >= right) {
System.out.println("数组左下标大于等于右下标，return");
return;
}
int pivot = a[left];
System.out.println("基值pivot=" + pivot);
int i = left;
int j = right;
while (i < j) {
while (pivot <= a[j] && i < j) {
System.out.println("右边起————a[" + j + "]=" + a[j] + "大于等于pivot不满足条件，做j--操作");
j--;
}
while (pivot >= a[i] && i < j) {
System.out.println("左边起————a[" + i + "]=" + a[i] + "小于等于pivot不满足条件，做i--操作");
i++;
}
if (i < j) {
int value = a[i];
a[i] = a[j];
a[j] = value;
System.out.println(a[i] + "和" + a[j] + "互换,互换后数组：" + Arrays.toString(a));
}
}
System.out.println("左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值" + pivot + "和分界线值" + a[i] + "交换");
a[left] = a[i];
a[i] = pivot;
System.out.println("基值和分界线值交换后数组：" + Arrays.toString(a));
quickSortTest(a, left, i - 1);
quickSortTest(a, i + 1, right);
}
打印出来log
初始数组[7, 5, 3, 2, 9, 10, 8, 4, 6, 1]左边起始下标0右边起始下标9
基值pivot=7
左边起————a[0]=7小于等于pivot不满足条件，做i--操作
左边起————a[1]=5小于等于pivot不满足条件，做i--操作
左边起————a[2]=3小于等于pivot不满足条件，做i--操作
左边起————a[3]=2小于等于pivot不满足条件，做i--操作
1和9互换,互换后数组：[7, 5, 3, 2, 1, 10, 8, 4, 6, 9]
右边起————a[9]=9大于等于pivot不满足条件，做j--操作
左边起————a[4]=1小于等于pivot不满足条件，做i--操作
6和10互换,互换后数组：[7, 5, 3, 2, 1, 6, 8, 4, 10, 9]
右边起————a[8]=10大于等于pivot不满足条件，做j--操作
左边起————a[5]=6小于等于pivot不满足条件，做i--操作
4和8互换,互换后数组：[7, 5, 3, 2, 1, 6, 4, 8, 10, 9]
右边起————a[7]=8大于等于pivot不满足条件，做j--操作
左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值7和分界线值4交换
基值和分界线值交换后数组：[4, 5, 3, 2, 1, 6, 7, 8, 10, 9]
初始数组[4, 5, 3, 2, 1, 6, 7, 8, 10, 9]左边起始下标0右边起始下标5
基值pivot=4
右边起————a[5]=6大于等于pivot不满足条件，做j--操作
左边起————a[0]=4小于等于pivot不满足条件，做i--操作
1和5互换,互换后数组：[4, 1, 3, 2, 5, 6, 7, 8, 10, 9]
右边起————a[4]=5大于等于pivot不满足条件，做j--操作
左边起————a[1]=1小于等于pivot不满足条件，做i--操作
左边起————a[2]=3小于等于pivot不满足条件，做i--操作
左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值4和分界线值2交换
基值和分界线值交换后数组：[2, 1, 3, 4, 5, 6, 7, 8, 10, 9]
初始数组[2, 1, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标0右边起始下标2
基值pivot=2
右边起————a[2]=3大于等于pivot不满足条件，做j--操作
左边起————a[0]=2小于等于pivot不满足条件，做i--操作
左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值2和分界线值1交换
基值和分界线值交换后数组：[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标0右边起始下标0
数组左下标大于等于右下标，return
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标2右边起始下标2
数组左下标大于等于右下标，return
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标4右边起始下标5
基值pivot=5
右边起————a[5]=6大于等于pivot不满足条件，做j--操作
左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值5和分界线值5交换
基值和分界线值交换后数组：[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标4右边起始下标3
数组左下标大于等于右下标，return
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标5右边起始下标5
数组左下标大于等于右下标，return
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标7右边起始下标9
基值pivot=8
右边起————a[9]=9大于等于pivot不满足条件，做j--操作
右边起————a[8]=10大于等于pivot不满足条件，做j--操作
左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值8和分界线值8交换
基值和分界线值交换后数组：[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标7右边起始下标6
数组左下标大于等于右下标，return
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 10, 9]左边起始下标8右边起始下标9
基值pivot=10
左边起————a[8]=10小于等于pivot不满足条件，做i--操作
左边的下标大于等于右边的下标了，说明数组需要判断的数据已经判断完一遍了，把基值10和分界线值9交换
基值和分界线值交换后数组：[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]左边起始下标8右边起始下标8
数组左下标大于等于右下标，return
初始数组[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]左边起始下标10右边起始下标9
数组左下标大于等于右下标，return
1 2 3 4 5 6 7 8 9 10
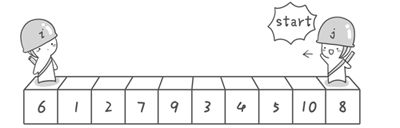
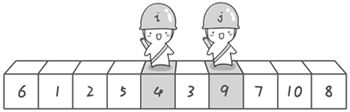
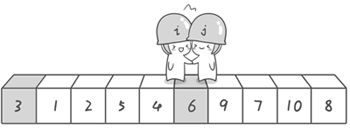
结合log捋一遍代码，快速排序的过程就明白了。后来在网上看到了一个图解，非常形象。博客地址https://blog.csdn.net/adusts/article/details/80882649
image.png
image.png
image.png
image.png
image.png
image.png
image.png
image.png
这个图解非常的形象，对此产生了浓厚的兴趣，搜索发现这个是《啊哈！算法》这本书的图解，准备买一本看看。
快速排序上面介绍的是不动基准数的思想，还有种是将基准数a[0]一开始就参与其中https://blog.csdn.net/MoreWindows/article/details/6684558这篇文章看完感觉讲的很好。
根据上面文章所表达的“填坑”思想，练一下手，用栈的方式书写一遍代码
public void quickSortStack(int[] a) {
Stack stack = new Stack<>();
stack.push(0);
stack.push(a.length - 1);
while (!stack.empty()) {
int right = stack.pop();
int left = stack.pop();
int pivot = a[left];
int i = left;
int j = right;
while (i < j) {
while (a[j] > pivot && i < j) {
j--;
}
if (i < j) {
a[i] = a[j];
i++;
}
while (a[i] < pivot && i < j) {
i++;
}
if (i < j) {
a[j] = a[i];
j--;
}
}
a[i] = pivot;
if (left < i - 1) {
stack.push(left);
stack.push(i - 1);
}
if (right > i + 1) {
stack.push(i + 1);
stack.push(right);
}
}
}