Google TensorFlow程序员点赞的文章!
前言
目录:
- 向量表示以及它的维度
- rnn cell
- rnn 向前传播
重点关注:
- 如何把数据向量化的,它们的维度是怎么来的
- 一共其实就是两步: 单个单元的rnn计算,拉通来的rnn计算
在看本文前,可以先看看这篇文章回忆一下:
吴恩达deepLearning.ai循环神经网络RNN学习笔记(理论篇)
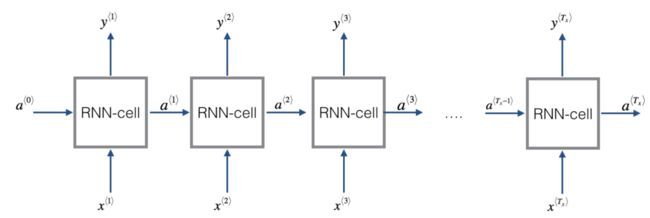
我们将实现以下结构的RNN,在这个例子中 Tx = Ty。
向量表示以及它的维度
Input with nx number of units
-
对单个输入样本,x(i) 是一维输入向量。
-
用语言来举个例子,将具有5k个单词词汇量的语言用one-hot编码成具有5k个单位的向量,所以 x(i) 的维度是(5000,)。
-
我们将用符号 nx 表示单个训练样本的单位数。
Batches of size m
-
如果我们取小批量(mini-batches),每个批次有20个训练样本。
-
为了受益于向量化,我们将20个样本 x(i) 变成一个2维数组(矩阵)。
-
比如一个维度是(5000,20)的向量。
-
我们用m来表示训练样本的数量。
-
所以小批量训练数据的维度是 (nx, m)。
Time steps of size Tx
-
循环神经网络有多个时间步骤,我们用t来表示。
-
我们将看到训练样本 x(i) 将经历多个时间步骤 Tx, 比如如果有10个时间步骤,那么 Tx = 10。
3D Tensor of shape (nx, m, Tx)
-
输入x就是用维度是 (nx, m, Tx) 的三维张量来表示。
Taking a 2D slice for each time step:
-
每一个时间步骤,我们用小批量训练样本(不是单个的训练样本)。
-
所以针对每个时间步骤t,我们用维度是 (nx, m)的2维切片。
-
我们把它表示成xt。
隐藏状态a的维度
-
a的定义: 从一个时间步骤到另一个时间步骤的激活值 at, 我们把它叫做隐藏状态。
-
同输入张量 x 一样,对于单个训练样本的隐藏状态,它的向量长度是na。
-
如果我们是包含了m个训练样本的小批量数据,那么小批量维度是 (na, m)。
-
如果我们把时间步加进去,那么隐藏状态的维度就是 (na, m, Tx)。
-
我们将用索引t来遍历时间步,每次操作是从3维张量切片成的2维向量。
-
我们用at来表示2维的切片,它的维度是 (na, m)。
预测值y^的维度
-
同输入x和隐藏状态一样,y^是一个维度是 (ny, m, Ty) 的3维张量。
-
ny: 代表预测值的单位数。
-
m: 小批次训练的样本数量。
-
Ty: 预测的时间数。
-
比如单个时间步 t,2维的切片 y^ 的维度是 (ny, m)。
RNN cell
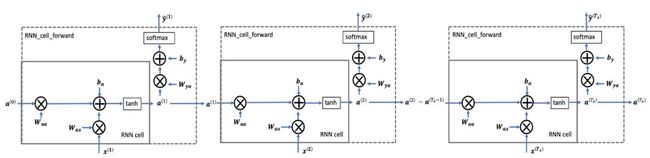
我们的第一个任务就是执行单个时间步骤的计算,计算如下图。
输入是a^
-
取出参数。
-
计算at。
-
计算yt^。
-
返回输出的at, yt^,还要存储一些值缓存起来。
import numpy as np
def rnn_cell_forward(xt, a_prev, parameters):
"""
Implements a single forward step of the RNN-cell as described in Figure (2)
Arguments:
xt -- your input data at timestep "t", numpy array of shape (n_x, m).
a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m)
parameters -- python dictionary containing:
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x) Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias, numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a_next -- next hidden state, of shape (n_a, m)
yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m)
cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters)
"""
# 取计算的参数
Wax = parameters["Wax"]
Waa = parameters["Waa"]
Wya = parameters["Wya"]
ba = parameters["ba"]
by = parameters["by"]
# 用公式计算下一个单元的激活值
a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
# 计算当前cell的输出
yt_pred = softmax(np.dot(Wya, a_next) + by)
# 用于向后传播的缓存值
cache = (a_next, a_prev, xt, parameters)
return a_next, yt_pred, cache
RNN向前传播
-
一个循环神经网络就是不断的重复你上面创建的rnn 单元。
-
如果你的输入数据序列是10个时间步,那么你就要重复你的rnn cell 10次。
-
在每个时间步中,每个单元将用2个输入:
-
a
: 前一个单元的隐藏状态。 -
xt: 当前时间步的输入数据。
-
每个时间步有两个输出:
-
一个隐藏状态at
-
一个测值y^⟨t⟩
-
权重和偏差 (Waa,ba,Wax,bx) 将在每个时间步中循环使用,它们保存在"parameters"的变量中。
def rnn_forward(x, a0, parameters):
"""
Implement the forward propagation of the recurrent neural network described in Figure (3).
Arguments:
x -- Input data for every time-step, of shape (n_x, m, T_x).
a0 -- Initial hidden state, of shape (n_a, m)
parameters -- python dictionary containing:
Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
ba -- Bias numpy array of shape (n_a, 1)
by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
Returns:
a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x)
y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x)
caches -- tuple of values needed for the backward pass, contains (list of caches, x)
"""
# 用于存储所有cache的列表,初始化它
caches = []
# 取一些纬度值,用于后面初始化变量
n_x, m, T_x = x.shape
n_y, n_a = parameters["Wya"].shape
# 初始化 a 和 y_pred
a = np.zeros((n_a, m, T_x))
y_pred = np.zeros((n_y, m, T_x))
# 初始化 a_next
a_next = a0
# loop over all time-steps of the input 'x'
for t in range(T_x):
# Update next hidden state, compute the prediction, get the cache
xt = x[:,:,t] # 通过切片的方式从输入变量x中取出当前t时间步的输入xt
a_next, yt_pred, cache = rnn_cell_forward(xt, a_next, parameters)
# 保存当前单元计算的a_next值
a[:,:,t] = a_next
# 保存当前单元的预测值y
y_pred[:,:,t] = yt_pred
# 添加每个单元的缓存值
caches.append(cache)
# store values needed for backward propagation in cache
caches = (caches, x)
return a, y_pred, caches
恭喜你(*^▽^*),到这里你已经能够从0到1的构建循环神经网络的向前传播过程。
在现代深度学习框架中,您仅需实现前向传递,而框架将处理后向传递,因此大多数深度学习工程师无需理会后向传递的细节。我就不写向后传播了。