查找
顺序查找 sequential search
无序表的顺序查找
def sequentialSearch(alist, item):
pos = 0
found = False
while pos < len(alist) and not found:
if alist[pos] == item:
found = True
pos += 1
return found
testlist = [3, 8, 5, 9, 7]
print(sequentialSearch(testlist,5))有序表的顺序查找
def orderedSequentialSearch(alist,item):
pos = 0
found = False
stop = False
while pos < len(alist) and not found and not stop:
if alist[pos] == item:
found = True
if alist[pos] > item:
stop = True
pos += 1
return found
testlist = [10, 20, 30, 40, 50, 60, 70]
print(orderedSequentialSearch(testlist,35))二分搜索
它也是分治策略,是将有序表分裂两半后在分裂后的小范围进行搜索。
def binarySearch(alist,item):
first = 0
found = False
last = len(alist) - 1
while first <= last and not found:
print(first, last)
midPos = (first + last) // 2
if item == alist[midPos]:
found = True
else:
if item < alist[midPos]:
last = midPos - 1
else:
first = midPos + 1
return found
testlist = [10, 20, 30, 40, 50, 60, 70]
print(binarySearch(testlist, 35))二分搜索的递归解法
def binarySearch2(alist,item):
if len(alist) == 0:
return False
else:
midPos = len(alist) // 2
if item == alist[midPos]:
return True
else:
if item < alist[midPos]:
binarySearch2(alist[:midPos], item)
else:
binarySearch2(alist[midPos+1:], item)
testlist = [10, 20, 30, 40, 50, 60, 70]
print(binarySearch2(testlist, 20))排序
1 冒泡排序
冒泡法的时间复杂度为O(n^2)
def bubbleSort(alist):
for passnum in range(len(alist)-1,0,-1):
for i in range(passnum):
if alist[i] > alist[i+1]:
alist[i+1], alist[i] = alist[i], alist[i+1]
testlist = [3, 8, 5, 9, 7]
bubbleSort(testlist)冒泡排序的一种优化方案
def bubbleSort2(alist):
exchange = True
passnum = len(alist) - 1
while passnum > 0 and exchange:
exchange = False
for i in range(passnum):
if alist[i] > alist[i+1]:
alist[i+1], alist[i] = alist[i], alist[i+1]
exchange = True
testlist = [3, 8, 5, 9, 7]
bubbleSort2(testlist)
print(testlist)2 选择排序
选择排序是冒泡的一种演变,比较的时间复杂度为O(n^2),交换的时间复杂度为O(n),仅少了交换的次数。
def selectionSort(alist):
i = 0
while i < len(alist):
j = i + 1
minIndex = i
while j < len(alist):
if alist[j] < alist[minIndex]:
minIndex = j
j += 1
alist[i], alist[minIndex] = alist[minIndex], alist[i]
i += 1
testlist = [3, 8, 5, 9, 7]
selectionSort(testlist)
print(testlist)选择排序的另一种解法:
def selectionSort2(alist):
for passnum in range(len(alist)-1, 0, -1):
maxIndex = 0
for i in range(passnum):
if alist[i + 1] > alist[maxIndex]:
maxIndex = i + 1
alist[passnum], alist[maxIndex] = alist[maxIndex], alist[passnum]
testlist = [3, 8, 5, 9, 7, 2]
selectionSort2(testlist)
print(testlist)3 插入排序
插入排序比对大小的复杂度还是O(n^2), 但性能会略优。插入排序每次会将 前面一个位置的值与待插入值比较大小;如果它比待插入值大则将前一个位置后移,否则中断对比大小,将当前值插入到这个位置。所以如果列表本身有序,它比较的次数大大降低。
def insertSort(alist):
for index in range(1, len(alist)):
currentValue = alist[index]
position = index
while position > 0 and alist[position - 1] > currentValue:
if alist[position - 1] > currentValue:
alist[position] = alist[position - 1]
position -= 1
alist[position] = currentValue
testlist = [3, 8, 5, 9, 7, 2]
insertSort(testlist)
print(testlist)4 谢尔(希尔)排序
谢尔(希尔)排序先将原列表分成每两个元素为一组的多个子列表,然后对子列表插入排序;然后再对原列表分成每四个元素为一组的多个子列表,然后对子列表插入排序;... 一直到对原列表划分单独一个子列表时,再进行插入排序;最终得到最后结果。一般的间隔设置从n/2、n/4、n/8...到1结束。无效的对比次数大大降低,复杂度在O(n)与O(n^2)之间,约为O(n^(3/2))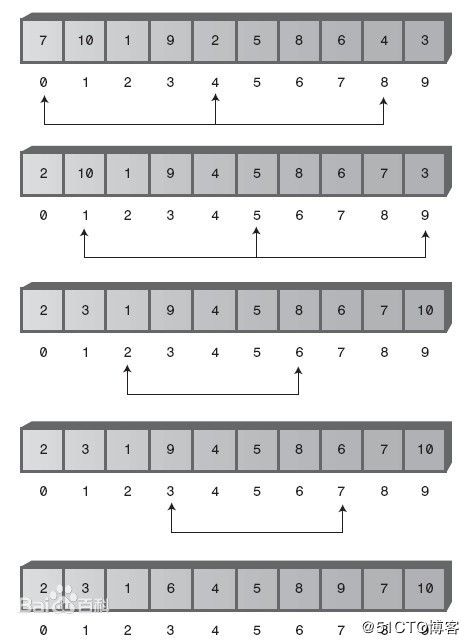
def shellSort(alist):
sublistcount = len(alist) // 2 #设置间隔
while sublistcount > 0:
for startposition in range(sublistcount):
gapInsertionSort(alist, startposition, sublistcount)
sublistcount = sublistcount // 2 #不断缩小间隔
def gapInsertionSort(alist, start, gap): #该函数完成子列表的排序
for i in range(start + gap, len(alist), gap):
currentValue = alist[i]
position = i
while position >= gap and alist[position - gap] > currentValue:
alist[position] = alist[position - gap]
position = position - gap
alist[position] = currentValue
testlist = [3, 8, 5, 9, 7, 2]
shellSort(testlist)
print(testlist)5 归并排序
归并排序是分治策略的一种; 它对原列表进行持续分裂,然后对分裂后的两半部分分别排序,再合并排序; 是一种递归思想。时间复杂度为O(n),但浪费了一倍的存储空间。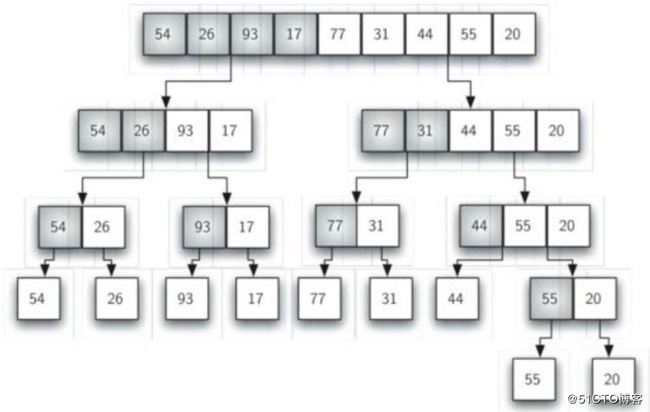
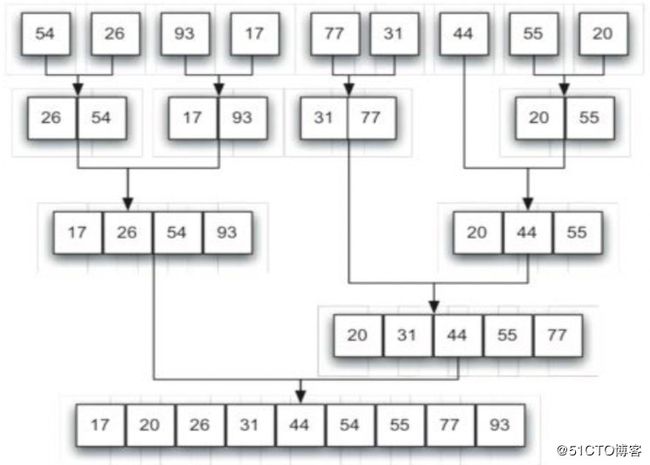
def mergeSort(alist):
if len(alist) > 1:
mid = len(alist) // 2
lefthalf = alist[:mid]
righthalf = alist[mid:]
mergeSort(lefthalf)
mergeSort(righthalf)
i = j = k = 0
while i < len(lefthalf) and j < len(righthalf):
if lefthalf[i] < righthalf[j]:
alist[k] = lefthalf[i]
i += 1
else:
alist[k] = righthalf[j]
j += 1
k += 1
while i < len(lefthalf):
alist[k] = lefthalf[i]
i += 1
k += 1
while j < len(righthalf):
alist[k] = righthalf[j]
j += 1
k += 1
testlist = [3, 8, 5, 9, 7, 2]
mergeSort(testlist)
print(testlist)归并排序的递归解法:
def merge_sort(alist):
if len(alist) <= 1:
return alist
mid = len(alist) // 2
left = alist[:mid]
right = alist[mid:]
return merge(merge_sort(left), merge_sort(right))
def merge(left, right):
result = []
while left and right:
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
result.extend(right if right else left)
return result
# testlist = [3, 8, 5, 9, 7, 2]
# print(merge_sort(testlist))6 快速排序
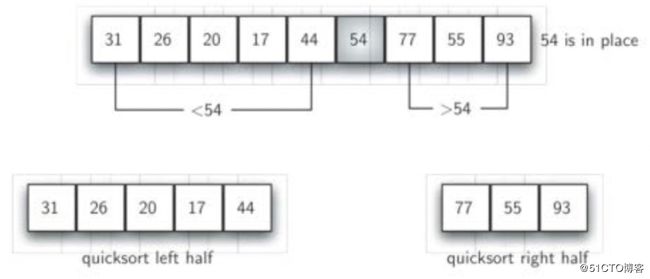
快速排序依据一个"中值"的数据项来把原始列表分为两半(分捡分裂), 然后每个部分进行快速排序。
分裂的目标是找到"中值",具体操作:
- 将第一项的右侧(下一个)设置为leftmark; 将它的左侧(上一个)设置为rightmark;
- 然后 leftmark向右移动,当遇到比第一项值大时stop; rightmark向左移动,当遇到比第一项值小时stop;
- 然后 leftmark与rightmark所指的位置进行数据交换;
- 然后 leftmark、rightmark继续移动; 直到leftmark移动到rightmark的右侧时stop;
- 此时 rightmark所指的位置就应该是"中值"所在的位置,然后把第一项和rightmark的数据进行交换;
如果分裂可以将数据表平均分为相等的两部分,分裂的复杂度为O(logN);在极端情况下它的复杂度会退化为O(n^2)。整个对比和移动的复杂度为O(n); 整个过程中不需额外的存储空间。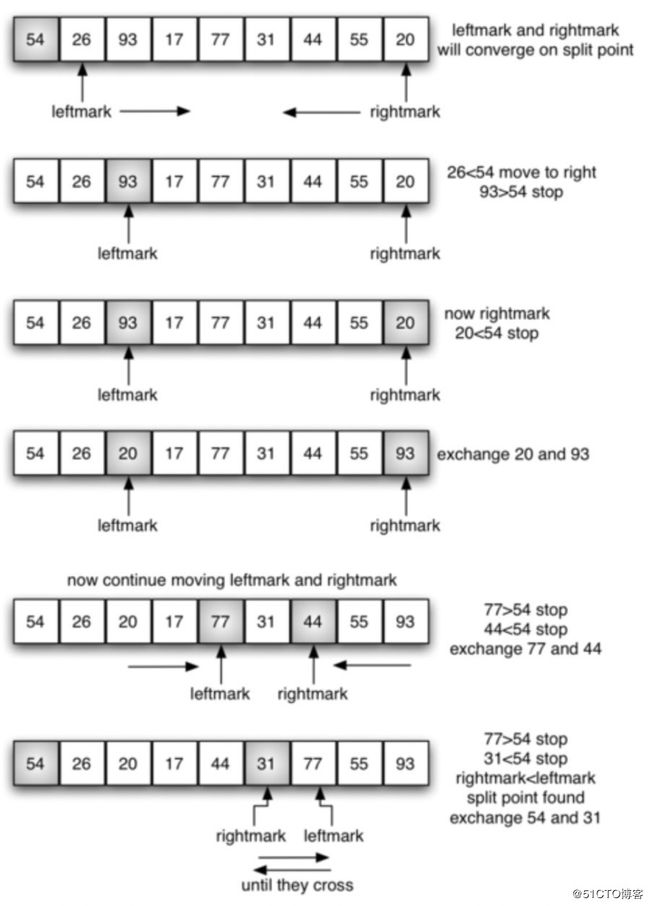
def partition(alist, first, last):
pivotvalue = alist[first]
leftmark = first + 1
rightmark = last
done = False
while not done:
while leftmark <= rightmark and alist[leftmark] <= pivotvalue:
leftmark = leftmark + 1
while rightmark >= leftmark and alist[rightmark] >= pivotvalue:
rightmark = rightmark -1
if rightmark < leftmark:
done = True
else:
alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]
alist[first], alist[rightmark] = alist[rightmark], alist[first]
return rightmark # 此时rightmark指向分裂点
def quickSortHelper(alist, first, last):
if first < last: # 列表中起码要有两个元素 才能分裂
splitpoint = partition(alist, first, last)
quickSortHelper(alist, first, splitpoint - 1)
quickSortHelper(alist, splitpoint + 1, last)
def quickSort(alist):
quickSortHelper(alist, 0, len(alist)-1)
testlist = [3, 8, 5, 9, 7, 2]
quickSort(testlist)
print(testlist)7 计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。计数排序(Counting sort) 是一种稳定的排序算法。
def countSort(alist):
maxValue = max(alist)
minValue = min(alist)
bucket = [0] * (maxValue - minValue + 1)
for item in alist:
bucket[item - minValue] += 1
alist.clear()
for index, count in enumerate(bucket):
while count > 0:
alist.append(index + minValue) #重新回填排序后的值
count -= 1
return alist
testlist = [73, 22, 93, 43, 55, 14, 28, 65, 39, 81]
countSort(testlist)
print(testlist)8 桶排序
桶排序与计数排序类似,但可以解决非整数的排序;桶排序相当于把计数数组划分为按顺序的几个部分;每一部分叫做一个桶,它来存放处于该范围内的数;然后再对每个桶内部进行排序,可以使用其他排序方法如快速排序,最后整个桶数组就是排列好的数据,再将其返回给原序列
def bucketSort(alist):
minValue = min(alist)
maxValue = max(alist)
bucketSize = (maxValue - minValue) / len(alist)
buckets = [ [] for i in range(len(alist) + 1) ]
for item in alist:
buckets[int((item - minValue) // bucketSize)].append(item)
alist.clear()
# print(buckets)
for sublist in buckets:
if len(sublist) > 0:
for item in quickSort(sublist):
alist.append(item)
return alist
testlist = [73, 22, 93, 43, 55, 14, 28, 65, 39, 81]
bucketSort(testlist)
print(testlist)9 基数排序
基数排序也是非比较的排序算法,对每一位进行排序,从最低位开始排序,复杂度为O(kn),为数组长度,k为数组中的数的最大的位数;基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。
def radixSort(alist):
maxValue=max(alist)
bit = 1
while bit<= len(str(maxValue)):
buckets = [[] for bit in range(11)]
for item in alist:
if(len(str(item)) < bit):
buckets[0].append(item)
else:
buckets[int(str(item)[-bit])].append(item)
alist.clear()
for bucket in buckets:
if len(bucket) > 0:
for item in bucket:
alist.append(item)
buckets.clear()
bit += 1
return alist
testlist = [73, 22, 93, 43, 55, 14, 28, 65, 39, 81, 8, 111]
radixSort(testlist)
print(testlist)10 堆排序
堆排序是一种二叉树结构, 在后期博客"树"中介绍。
注: 纯属个人笔记,不喜勿喷。