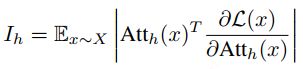bert剪枝系列——Are Sixteen Heads Really Better than One?

1，概述

　　剪枝可以分为两种：一种是无序的剪枝，比如将权重中一些值置为0，这种也称为稀疏化，在实际的应用上这种剪枝基本没有意义，因为它只能压缩模型的大小，但很多时候做不到模型推断加速，而在当今的移动设备上更多的关注的是系统的实时相应，也就是模型的推断速度。另一种是结构化的剪枝，比如卷积中对channel的剪枝，这种不仅可以降低模型的大小，还可以提升模型的推断速度。剪枝之前在卷积上应用较多，而随着bert之类的预训练模型的出现，这一类模型通常比较大，且推断速度较慢。例如bert在文本分类的任务上，128的序列长度，其推断速度都只有80ms左右，这还只是单个模型，而一个大的系统，往往是有多个模型组成的。因此bert要想在工业界，尤其是移动端落地，是极度需要模型压缩的。

2，具体方法

　　看完这篇论文之后，更多的感觉是这篇论文并没有在剪枝上有太多的贡献，更像是对multi head中head的数量做了一个实验性的工作，探索了在multi head中并不是所有的head都需要，有很多head提取的信息对最终的结果并没有什么影响，是冗余存在的。

　　本论文在探讨在test阶段，去掉一部分head是否会影响模型的性能，得到的结论是大多数都不会，而且部分还会提升性能，作者给出了三种实验方法来证明这一点：

　　1，每次去掉一层中一个head，测试模型的性能

　　2，每次去掉一层中剩余的层，只保存一个head，测试模型的性能

　　3，通过梯度来判断每个head的重要性，然后去掉一部分不重要的head，测试模型的性能

　　为了实现上述的实验，作者对multi head的计算做了一些修改，修改后的公式如下：

　　　　

　　在这里引入了一个系数$\zeta_h$，该值的取值为0或1，它的作用是用来mask不重要的head。在训练时保持为1，到test的时候对部分head mask掉。

　　作者在基于transformer的机器翻译模型上和基于bert的NLI任务上做了实验，我们来看看上面三个实验的结果

　　Ablating One Head

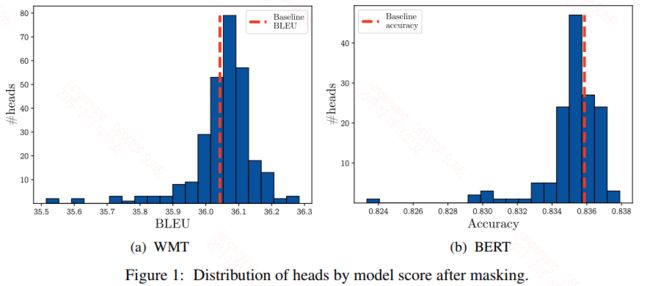
　　去掉一个head，作者给出了实验结果如下：

　　　　

 　　从上面的图中可以看到大多数head去掉之后的模型分数还基本分布在baseline附近，从作者给的表格数据看会更加的清晰：

　　　　

 　　上面给出的是机器翻译的表格数据，蓝色的值表示性能增加，红色的值表示性能下降，大多数情况下性能是增加的，只有少部分性能会有所下降，只有极少部分性能会下降的比较多。

　　Ablating All Heads but One

　　当去掉一层中的其余head只保留一个head时，我们来看下模型的结果，这回作者给出了一个离散图：

　　　　

 　　同样的，大多数情况下的性能都分布在baseline附近，同样看看表格会更清晰：

　　　　

 　　从上面来看除了机器翻译中的encoder-decoder之间的attention的最后一层会出现性能明显的下降，其他大多数情况都还好，甚至有的情况下性能反而上升。

　　上面两种实验都有一个共同的弊端，就是每次实验只能对一层做head的mask，但实际过程中所有层的head都有可能会被去除，且至于去除哪些还和层与层之间的依赖性有关，因此第三种方法可以来改善这个问题。

　　Head Importance Score for Pruning

　　在这里作者引入了梯度来衡量head的重要性，首先给出一个公式如下：

　　　　

 　　上面公式是对mask系数的偏导，我们知道偏导的值的大小可以衡量这个维度上对损失的影响大小，在这里作者对偏导取了个绝对值，避免在求期望的时候正负抵消，因为无论是正值还是负值，只要绝对值比较大，就可以衡量偏导对损失的影响是比较大的，这里的期望是对所有样本X的，因为单个batch是存在误差的，因此对全量样本计算的偏导求均值。

　　 对上面的公式做一个链式转换，可以得到：

　　　　

 　　这样我们就可以用这个对head的期望梯度值来衡量其重要性，然后按百分比去除head，得到的结果如下：

　　　　

 　　上面图中的实验是通过梯度来进行剪枝的，虚线是通过第一种方法中的分数来衡量head的重要性进行剪枝的，可以看到基于梯度的效果还是很明显的，但是剪枝范围也是有限的，超过这个范围之后，性能会急剧下降。

　　作者还测了下剪枝后模型的推断速度，个人感觉这个推断速度的减小真的是毫无意义：

　　　　

 　　如上图所示，只有在batch达到16的时候才有比较明显的速度提升，但是大多数线上运行的时候都是batch为1的。不过也不能就此下定论说减少head的数量是起不到加速效果的，个人感觉作者在这里测推断速度的时候是存在一些问题的：作者是先训练，后剪枝，但剪枝之后没有再训练，这也就意味着这些head仍然存在，只是将不需要的head前面的mask系数置为0而已。为什么做出这样的认定呢？因为在实际的multi head设计中，我们是要保证每个head得到的词向量拼接在一起等于原始的词向量，因为后面要进入到前向层，必须保持维度一致，我猜这里作者可能是将mask掉的head得到的向量置为0，这样这些值在下一层计算self-attention就没有意义了，至于为什么还是有加速，原因不明。以上个人猜测。

　　此外单纯得减少head的数量好像对加速意义不大，只有配合减小embedding size才有意义，否则计算复杂度基本一致，因为我们在做multi-attention时映射到不同子空间时，实际上是一个大的矩阵映射，这个大的矩阵的维度取决于embedding size，映射完之后再分割成多个而已。从计算上来看self-attention是耗时的，因为减少embedding size，减小序列长度都可以极大的提速（减小序列长度还会影响到前向层的速度）。