版权所有。转载请保留作者和原文链接信息。
描述性统计分析是是对数据的探索和了解,也是数据分析和数据挖掘的初步工作,常用到一些基本的统计指标和可视化图形来进行。
描述性统计分析基本统计量
衡量样本值的指标
平均值(mean)
用来衡量样本平均水平。
中位数(median)
亦即50%分位数,用来衡量样本处于中间的水平;平均水平和中等水平并不是一个概念,所以这2个统计指标有应用场景的不同。另外,平均值易受异常值影响,而中位数的鲁棒性较强,不易受异常值影响。
众数(mode)
出现频次最多的数值,表征大部分的水平。
衡量样本变异程度的统计量
方差(variance)和标准差(standard deviation)
> x <- rnorm(100)
> var(x)
[1] 0.9367542
> sum((x-mean(x))^2/(length(x)-1))
[1] 0.9367542
> sqrt(sum((x-mean(x))^2/(length(x)-1)))
[1] 0.9678606
> sd(x)
[1] 0.9678606
极差(range)和四分位距(interquartile range, IQR)
极差是最大值与最小值的差值,IQR是上四分位点与下四分位点的差值。这些差值,限定了大部分的样本差距。
偏度(skewness)
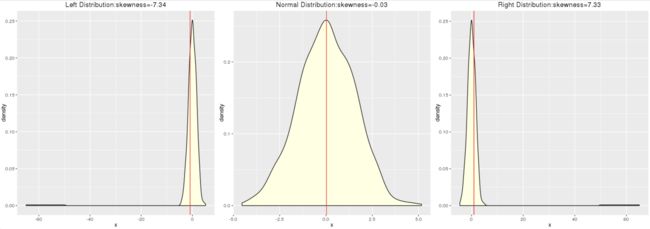
偏度是用来衡量样本分布整体偏离均值的程度。偏度计算公式如下,3阶中心矩。
对于标准正常分布来说,偏度为0;反映在曲线是以均值为轴左右对称;偏度越小于0,越左偏;越大于0越右偏。
skewness <- function(x){
return(mean(((x-mean(x))/sd(x))^3))
}
x <- 1:1000
y_norm <- rnorm(x,mean = 0,sd = 1.5) # 标准正态分布
skewness(y_norm)
y_right <- c(y_norm,50:65) # 加上一小部分偏大的异常值,使整体右偏
skewness(y_right)
y_left<- c(y_norm,-50:-65) # 加上一小部分偏小的异常值,使整体左偏
skewness(y_left)
p_norm <- ggplot(data.frame(x=y_norm),aes(x=x))+
geom_density(fill="lightyellow")+
geom_vline(xintercept = mean(y_norm),color="red")+
labs(title=paste('Normal Distribution:skewness=',round(skewness(y_norm),2),sep=""))+
theme(plot.title = element_text(hjust=0.5))
p_right <- ggplot(data.frame(x=y_right),aes(x=x))+
geom_density(fill="lightyellow")+
geom_vline(xintercept = mean(y_right),color="red")+
labs(title=paste('Right Distribution:skewness=',round(skewness(y_right),2),sep=""))+
theme(plot.title = element_text(hjust=0.5))
p_left <- ggplot(data.frame(x=y_left),aes(x=x))+
geom_density(fill="lightyellow")+
geom_vline(xintercept = mean(y_left),color="red")+
labs(title=paste('Left Distribution:skewness=',round(skewness(y_left),2),sep=""))+
theme(plot.title = element_text(hjust=0.5))
p_left+p_norm+p_right
- 标准正态分布:平均值 = 中位数
- 左偏分布:平均值 < 中位数
- 右偏分布:平均值 > 中位数
> # 正态分布
> mean(y_norm)
[1] 0.02306488
> median(y_norm)
[1] 0.03905866
>
> # 左偏分布
> mean(y_left)
[1] -0.8828102
> median(y_left)
[1] 0.01444451
>
> # 右偏分布
> mean(y_right)
[1] 0.9282135
> median(y_right)
[1] 0.06747427
峰度(kurtosis)
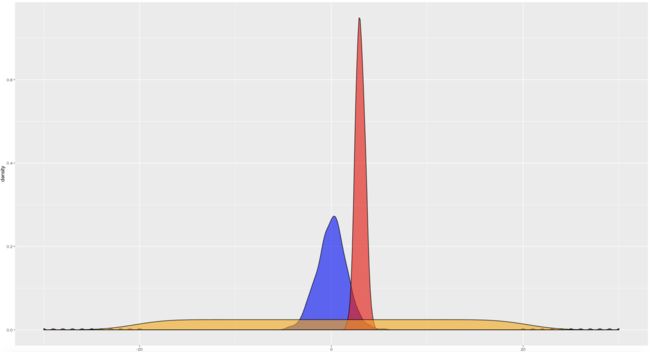
峰度用来衡量样本分布集中在众数附近的程度。峰度公式如下,4阶中心矩。
标准正态分布的峰度为3;峰度越大于3,则概率密度曲线越尖锐,表征大部分的样本都集中在众数附近;峰度越小于3,则概率密度曲线越平缓,表征大部分的样本均匀分散在众数两侧。
> x <- 1:1000
> y_norm <- rnorm(x,mean = 0,sd = 1.5) # 标准正态分布
> y_sharp <- c(rnorm(x,mean=3,sd=0.5),-30:-20,20:30) # 令大部分的样本集中在均值附近
> y_flat <- rep(-20:20,25) # 从-20:20循环25次
> kurtosis(y_norm)
[1] 3.251031
> kurtosis(y_sharp)
[1] 49.91396
> kurtosis(y_flat)
[1] 1.795064
> ggplot()+
+ geom_density(data=data.frame(x=y_norm),aes(x=x),fill="blue",alpha=0.6)+
+ geom_density(data=data.frame(x=y_sharp),aes(x=x),fill="red",alpha=0.6)+
+ geom_density(data=data.frame(x=y_flat),aes(x=x),fill="orange",alpha=0.6)
对比一下峰度和标准差的概念:峰度是用来衡量样本集中在众数密度的程度,本质是衡量样本分布的频率,对异常值不敏感;标准差是用来样本值之间整体的差异程度,不关注分布的频率,对异常值敏感。
协方差
协方差是衡量2个变量之间的一同的变化趋势,公式如下。
可以看到方差是协方差的特殊情况:当两个变量为同一个时,协方差就变成了方差。从公式中可以看到:如果变量x变大大于期望,y也在变大大于期望,则协方差系数大于0;若一个变大大于期望,另一个在减小小于期望,则协方差系数小于0。
协方差系数只能衡量2个变量的变化趋势,对于多个变量,则应构建协方差矩阵。
相关系数
协方差本身就可以衡量两个变量的相关性,Pearson相关系数则是在协方差的基础上再除以2个变量的标准差:
除以2个变量的标准差,实质上是标准化的过程,可以使得相关系数的范围介于-1到1之间。
相关系数r用来衡量2个变量的线性相关程度。当r > 0时,表明X和Y是正相关关系,且越接近于1,正相关性越强;r < 0时,表时X和Y是负相关关系,且越接近于-1,负相关性越强;r = 0 时,则表示X与Y没有相关性(独立一定相关系数一定为0,相关系数为0不一定独立)。
相关性和因果性
因果性必然有相关性,相关性不一定有因果性是上面那句独立一定相关系数一定为0,相关系数为0不一定独立的等价命题。一些小例子可以说明:
美国人口数据中,脚的尺寸与学历的相关系数大于0.8。能否说明脚越大的人学历越高?真实情况是样本主要分布于3岁到30岁人口的样本,脚的尺寸大小与年龄相关,而年龄与学历又高度相关。所以在3岁到30岁的人群中,年龄越大能说明学历越高,而不是由脚尺寸决定的。
医学数据中,吸烟与牙齿发黄的程度都与患肺癌的概率高度相关。但去清洗牙齿显然是无助于降低肺癌概率的,戒烟能能。因此吸烟与肺癌是有因果性,而牙齿发黄与患肺癌只有相关性没有因果性。
从上面的例子中可以看出,相关(除了数学上)的局限性在于,相关系数往往只能发现表层的现象,而不能说明本质联系。若自变量与因变量有因果性,那么在数据上反映的与相关的其他变量与一样有相关性——所以在探索性数据分析上,发现一堆与因变量高相关的变量,可能往往这些变量本身就存在着相关性。
从实践角度上来说,只有基于因果性才能制定对应的方针来提升指标,尽管这并不容易。那么怎么分析因果性?这是一个高深复杂的问题。实践中当然要基于业务经验来判断分析,但若缺乏科学、有说服力的方法来指导,往往又会沦为拍脑袋。也许就这是数据科学家的挑战和价值,学习、理解科学的理论方法,并用实践来改善经验主义驱动的业务发展模式。
描述性统计分析可视化图形
描述性统计分析中经常会用数据可视化图形来观察数据的基本特征与趋势,详见:《数据可视化基本套路总结》
参考资料
- 峰度
- 协方差
- 协方差矩阵有什么意义?
- 有哪些相关性不等于因果性的例子?
- 哪些统计方法可以用于判断因果关系?