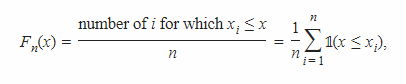《Modern Statistics for Modern Biology》Chapter 一: 离散数据模型的预测(1.1 - 1.3)
《Modern Statistics for Modern Biology》Chapter 一: 离散数据模型的预测(1.4 - 1.5)
《Modern Statistics for Modern Biology》Chapter 二: 统计建模(2.1-2.3)
《Modern Statistics for Modern Biology》Chapter 二: 统计建模(2.4-2.5)
《Modern Statistics for Modern Biology》Chapter 二 统计建模(2.6 - 2.7)
《Modern Statistics for Modern Biology》Chapter 二 统计建模(2.8 - 2.9)
《Modern Statistics for Modern Biology》Chapter 二 统计建模(2.10 完结)
《Modern Statistics for Modern Biology》Chapter 三:R语言中的高质量图形(3.1-3.4)
从这章开始最开始记录一些markdown等小知识
$\hat{p}=\frac{1}{12}$:
掌握R语言中的apply函数族
卡方检验
Hardy-Weinberg equilibrium( 哈迪-温伯格平衡 )
带你理解beta分布
简单介绍一下R中的几种统计分布及常用模型
- 统计分布每一种分布有四个函数:
d――density(密度函数),p――分布函数,q――分位数函数,r――随机数函数。比如,正态分布的这四个函数为dnorm,pnorm,qnorm,rnorm。下面我们列出各分布后缀,前面加前缀d、p、q或r就构成函数名:norm:正态,t:t分布,f:F分布,chisq:卡方(包括非中心)unif:均匀,exp:指数,weibull:威布尔,gamma:伽玛,beta:贝塔lnorm:对数正态,logis:逻辑分布,cauchy:柯西,binom:二项分布,geom:几何分布,hyper:超几何,nbinom:负二项,pois:泊松signrank:符号秩,wilcox:秩和,tukey:学生化极差
如何预测一条序列是否含有CpG岛
图片输出尽量保存为矢量图
结合setNames函数与scale_fill_manual函数来指定ggplot2的填充颜色(Figure 3.13)
要善于用stat_summary来自定义函数结合ggplot2进行绘图
3.5 图形语法
ggplot2的图形语法的组成部分是
- 一个或者多个数据集
- 作为数据的可视表示的一个或多个几何对象,例如,点、直线、矩形、等高线
- 描述如何将数据中的变量映射到几何对象的视觉特性(美学)和相关的比例(例如:线性,对数,秩)
- 一个或多个坐标系
- 统计总结规则
- 一种分面规范,即使用多个相似的子图来查看相同数据的子集。
- 影响布局和渲染的可选参数,如文本大小、字体和对齐方式、图例位置。
下面的代码针对相同的数据在同一图形中使用三种类型的几何对象:点、直线和置信带。
> BiocManager::install("Biobase", version = "3.8")
> library("Hiiragi2013")
> data("x")
> dim(Biobase::exprs(x))
> dftx = data.frame(t(Biobase::exprs(x)), pData(x))
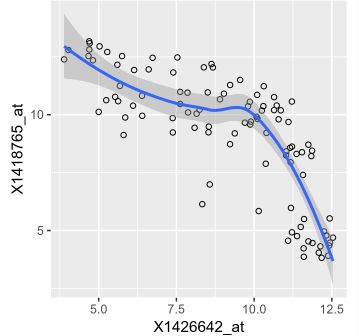
> ggplot( dftx, aes( x = X1426642_at, y = X1418765_at)) +
geom_point( shape = 1 ) +
geom_smooth( method = "loess" )
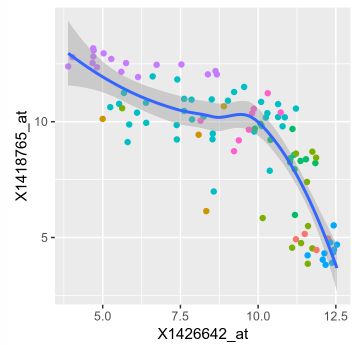
ggplot( dftx, aes( x = X1426642_at, y = X1418765_at )) +
geom_point( aes( color = sampleColour), shape = 19 ) +
geom_smooth( method = "loess" ) +
scale_color_discrete( guide = FALSE ) ## guide = FALSE 表示不添加图例
- 如果我们想找出哪些基因是这些探针标识符的目标,以及它们可能做什么,我们可以这样做:
> library("mouse4302.db")
> AnnotationDbi::select(mouse4302.db,
+ keys = c("1426642_at", "1418765_at"), keytype = "PROBEID",
+ columns = c("SYMBOL", "GENENAME"))
'select()' returned 1:1 mapping between keys and columns
PROBEID SYMBOL GENENAME
1 1426642_at Fn1 fibronectin 1
2 1418765_at Timd2 T cell immunoglobulin and mucin domain containing 2
- 如果使用的是
geom_smooth,那么ggplot2在默认情况下使用stat=“smooth”并显示一条线;如果使用geom_histogram,则对数据进行分bin,并以barplot格式显示结果。这里有一个例子:
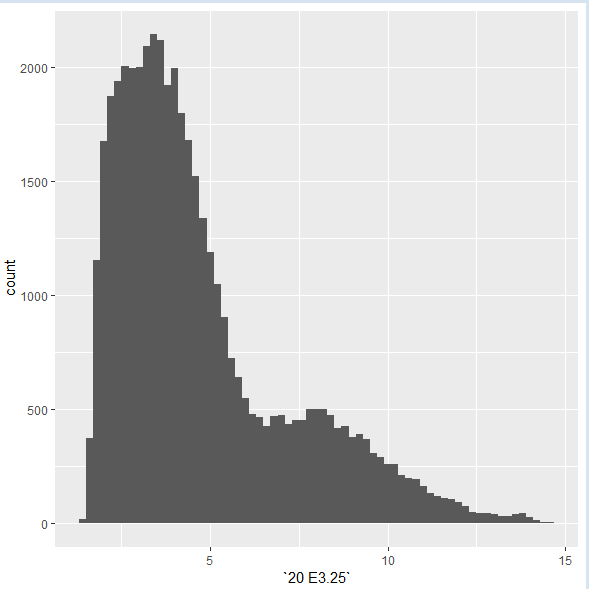
> dfx = as.data.frame(Biobase::exprs(x))
> ggplot(dfx, aes(x = `20 E3.25`)) + geom_histogram(binwidth = 0.2)
► 问题
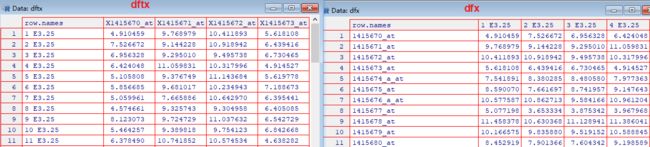
-
dfxanddftx有什么不同?为什么要创建两个?
我们回到之前的
barplot, 赋值给pb
> library("dplyr")
> groups = group_by(pData(x), sampleGroup) %>%
+ summarise(n = n(), color = unique(sampleColour))
> head(groups)
# A tibble: 6 x 3
sampleGroup n color
1 E3.25 36 #CAB2D6
2 E3.25 (FGF4-KO) 17 #FDBF6F
3 E3.5 (EPI) 11 #A6CEE3
4 E3.5 (FGF4-KO) 8 #FF7F00
5 E3.5 (PE) 11 #B2DF8A
6 E4.5 (EPI) 4 #1F78B4
> groupColor = setNames(groups$color, groups$sampleGroup)
> pb = ggplot(groups, aes(x = sampleGroup, y = n))
- 我们创建了一个绘图对象,如果我们要去展现
pb, 会得到这是一个空白的图形。因为我们没有指定任何特定的j几何对象。到目前为止,我们在pb对象中所拥有的只是数据和aesthetics。
> class(pb)
[1] "gg" "ggplot"
> pb
- 现在我们可以一层一层的添加图层。
> pb = pb + geom_bar(stat = "identity") ## 柱状图
> pb
> pb = pb + aes(fill = sampleGroup) ## 按group填充颜色
> pb
> pb = pb + theme(axis.text.x = element_text(angle = 90, hjust = 1)) # 设置x坐标标签,旋转90°
> pb
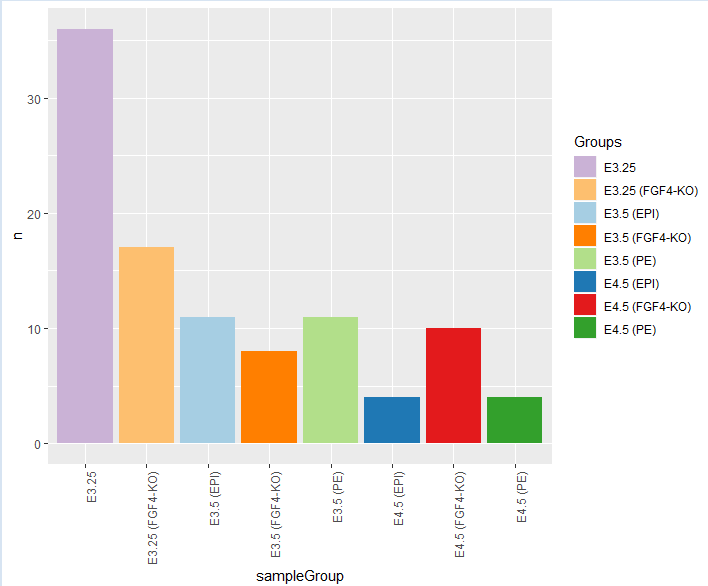
> pb = pb + scale_fill_manual(values = groupColor, name = "Groups") ## 指定填充颜色,注意要与sampleGroup一致
Error in rlang::is_missing(values) : 找不到对象'groupColor'
> groupColor = setNames(groups$color, groups$sampleGroup)
> pb = pb + scale_fill_manual(values = groupColor, name = "Groups")
> pb
> groups
# A tibble: 8 x 3
sampleGroup n color
1 E3.25 36 #CAB2D6
2 E3.25 (FGF4-KO) 17 #FDBF6F
3 E3.5 (EPI) 11 #A6CEE3
4 E3.5 (FGF4-KO) 8 #FF7F00
5 E3.5 (PE) 11 #B2DF8A
6 E4.5 (EPI) 4 #1F78B4
7 E4.5 (FGF4-KO) 10 #E31A1C
8 E4.5 (PE) 4 #33A02C
> groupColor
E3.25 E3.25 (FGF4-KO) E3.5 (EPI) E3.5 (FGF4-KO) E3.5 (PE) E4.5 (EPI) E4.5 (FGF4-KO) E4.5 (PE)
"#CAB2D6" "#FDBF6F" "#A6CEE3" "#FF7F00" "#B2DF8A" "#1F78B4" "#E31A1C" "#33A02C"
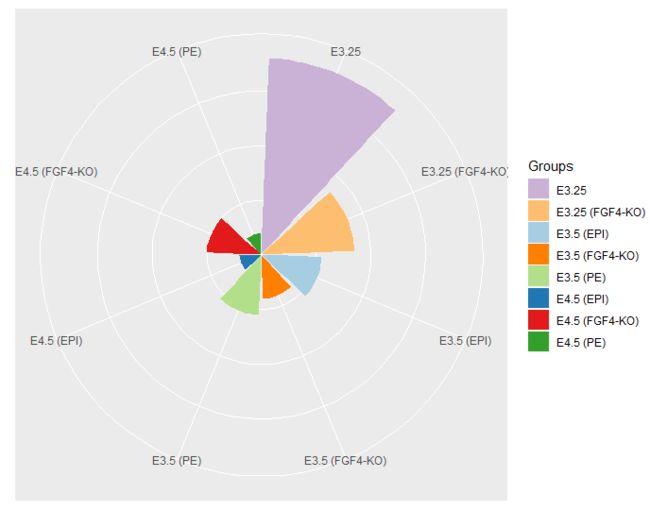
- 将柱状图转换为极坐标图
> pb.polar = pb + coord_polar() +
+ theme(axis.text.x = element_text(angle = 0, hjust = 1),
+ axis.text.y = element_blank(),
+ axis.ticks = element_blank()) +
+ xlab("") + ylab("")
> polar
请注意,我们可以通过简单地将它们设置为新值来覆盖以前设置的主题参数 - 无需返回重新创建pb,我们最初设置它们
3.6 一维数据的可视化
- 生物数据分析的一个共同的任务是比较几个样本的单变量测量。在本节中,我们将探索可视化和比较此类示例的一些可能性。作为示例,我们将使用四个基因
Fgf4、Gata4、GATA6和Sox2的强度。
> selectedProbes = c( Fgf4 = "1420085_at", Gata4 = "1418863_at",
+ Gata6 = "1425463_at", Sox2 = "1416967_at")
- 使用
reshape2包中的melt函数,提取四个基因在总的数据中对应的信息。
> library("reshape2")
> genes = melt(Biobase::exprs(x)[selectedProbes, ],
+ varnames = c("probe", "sample"))
> head(genes)
probe sample value
1 1420085_at 1 E3.25 3.027715
2 1418863_at 1 E3.25 4.843137
3 1425463_at 1 E3.25 5.500618
4 1416967_at 1 E3.25 1.731217
5 1420085_at 2 E3.25 9.293016
6 1418863_at 2 E3.25 5.530016
- 为了更好地衡量,我们还添加了一个列,该列提供了基因符号和探针标识符。
> genes$gene =
names(selectedProbes)[match(genes$probe, selectedProbes)]
> head(genes)
probe sample value gene
1 1420085_at 1 E3.25 3.027715 Fgf4
2 1418863_at 1 E3.25 4.843137 Gata4
3 1425463_at 1 E3.25 5.500618 Gata6
4 1416967_at 1 E3.25 1.731217 Sox2
5 1420085_at 2 E3.25 9.293016 Fgf4
6 1418863_at 2 E3.25 5.530016 Gata4
- 3.6.1
Barplot
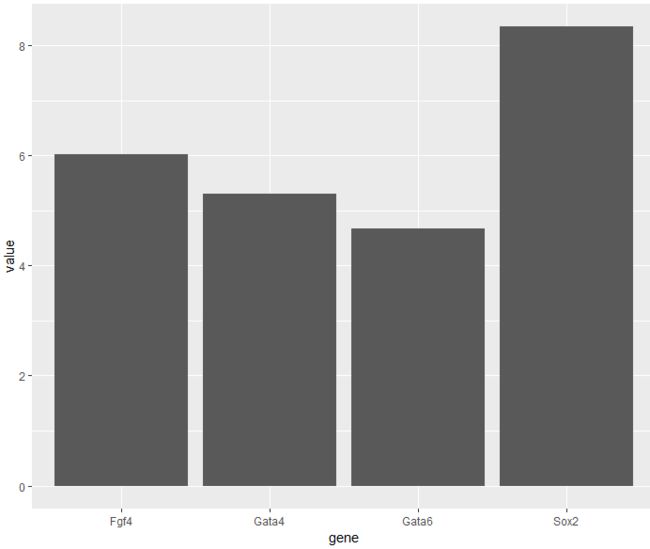
> ggplot(genes, aes( x = gene, y = value)) +
+ stat_summary(fun.y = mean, geom = "bar")
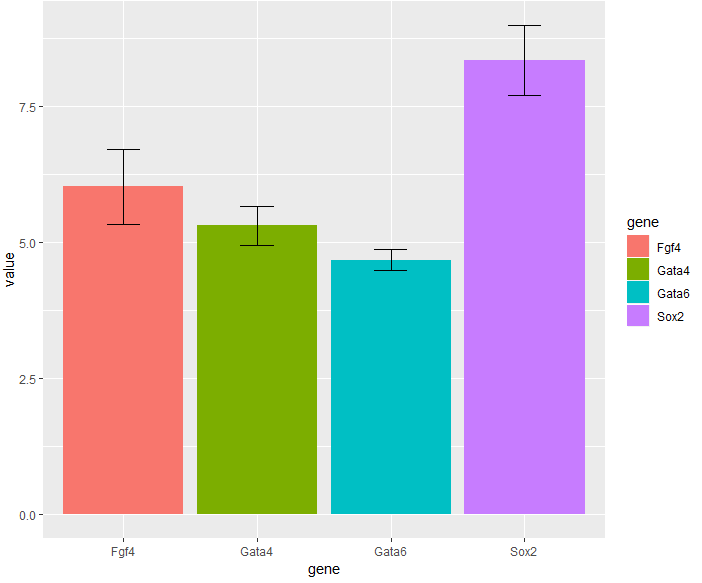
- 在Figure 3.15中我们呈现了各个基因的均值来绘制条形图。然而采用均值来绘制会使我们丢失掉很多信息。考虑到所需的空间量,条形图往往是一种可视化数据的糟糕方式。
- 有时候我们想要添加
误差线,实现如下:
> library("Hmisc")
> ggplot(genes, aes( x = gene, y = value, fill = gene)) +
+ stat_summary(fun.y = mean, geom = "bar") +
+ stat_summary(fun.data = mean_cl_normal, geom = "errorbar",
+ width = 0.25)
- 这里我们使用了两个统计函数
mean和mean_cl_normal以及两个几何对象bar和errorbar。mean_cl_normal函数来源于Hmisc 包——用来计算平均值的标准误差(或者置信区间)。
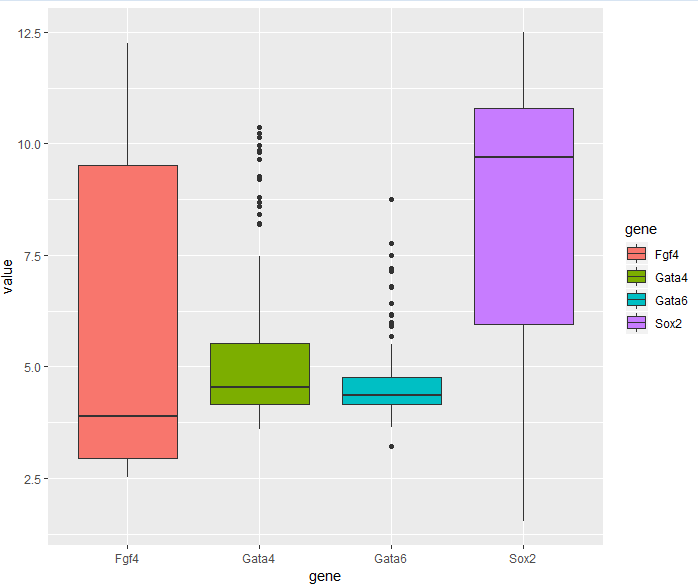
3.6.2 Boxplots
> p = ggplot(genes, aes( x = gene, y = value, fill = gene))
> p + geom_boxplot()
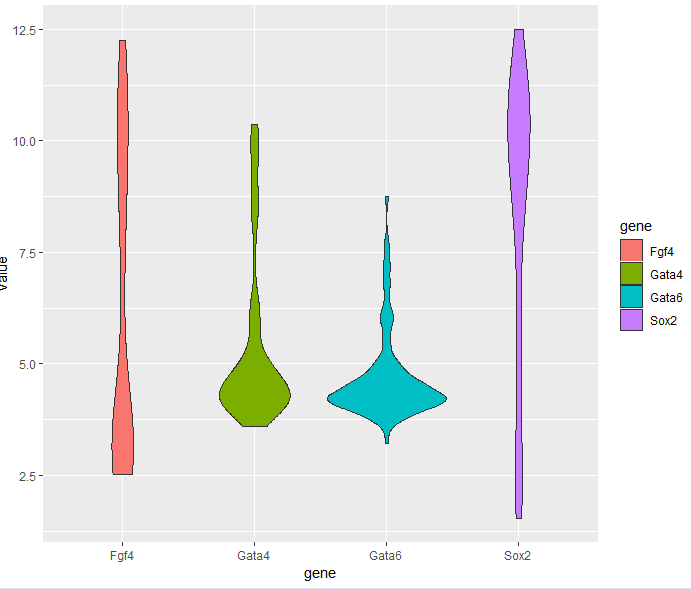
3.6.3 Violin plots
> p + geom_violin()
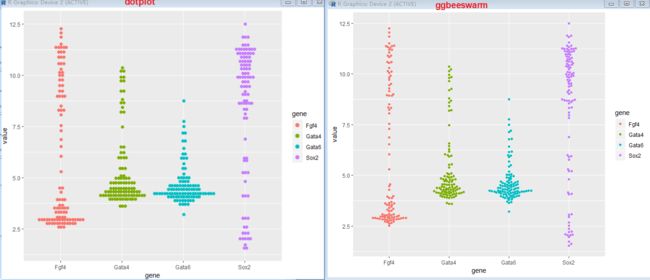
3.6.4 Dot plots and beeswarm plots
> p + geom_dotplot(binaxis = "y", binwidth = 1/6,
+ stackdir = "center", stackratio = 0.75,
+ aes(color = gene))
> library("ggbeeswarm")
> p + geom_beeswarm(aes(color = gene))
3.6.5 Density plots
> ggplot(genes, aes( x = value, color = gene)) + geom_density()
3.6.6 ECDF plots
- cumulative distribution function (CDF): 累积分布函数
F(x)=P(X≤x) - empirical cumulative distribution function (ECDF): 经验累积分布函数
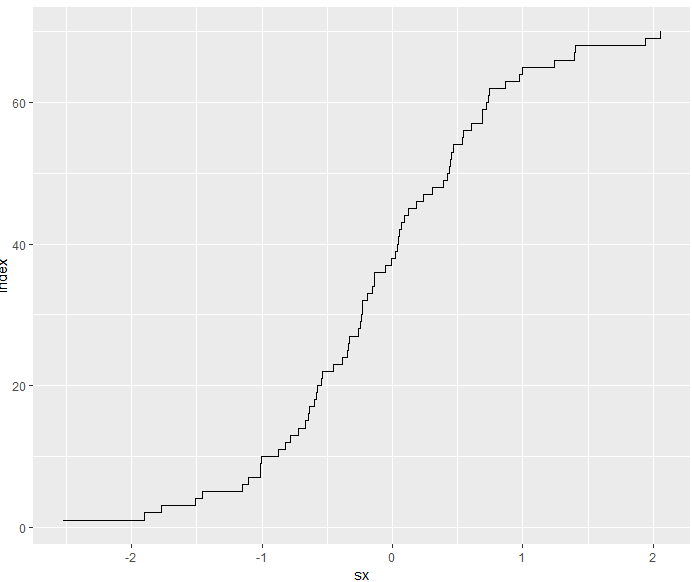
> simdata = rnorm(70)
> tibble(index = seq(along = simdata),
+ sx = sort(simdata)) %>%
+ ggplot(aes(x = sx, y = index)) + geom_step()
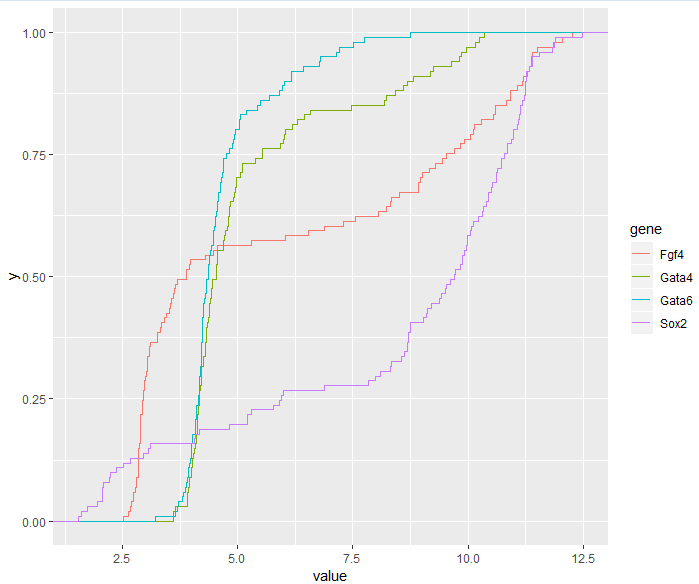
> ggplot(genes, aes( x = value, color = gene)) + stat_ecdf()
3.6.7 The effect of transformations on densities
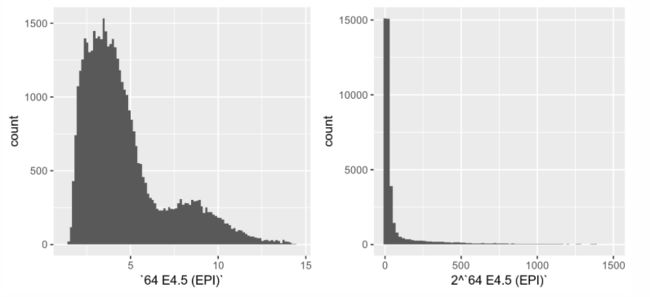
- 很容易观察直方图或密度图,并检查它们是否有双峰(或多模态)的证据,以表明某些潜在的生物现象。在此之前,重要的是要记住,
密度的模式的数量取决于数据的比例变换,通过链规则。例如,让我们查看来自Hiiragi数据集中的一个数组的数据
> ggplot(dfx, aes(x = `64 E4.5 (EPI)`)) + geom_histogram(bins = 100)
> ggplot(dfx, aes(x = 2 ^ `64 E4.5 (EPI)`)) +
+ geom_histogram(binwidth = 20) + xlim(0, 1500)