一、程序结构分析
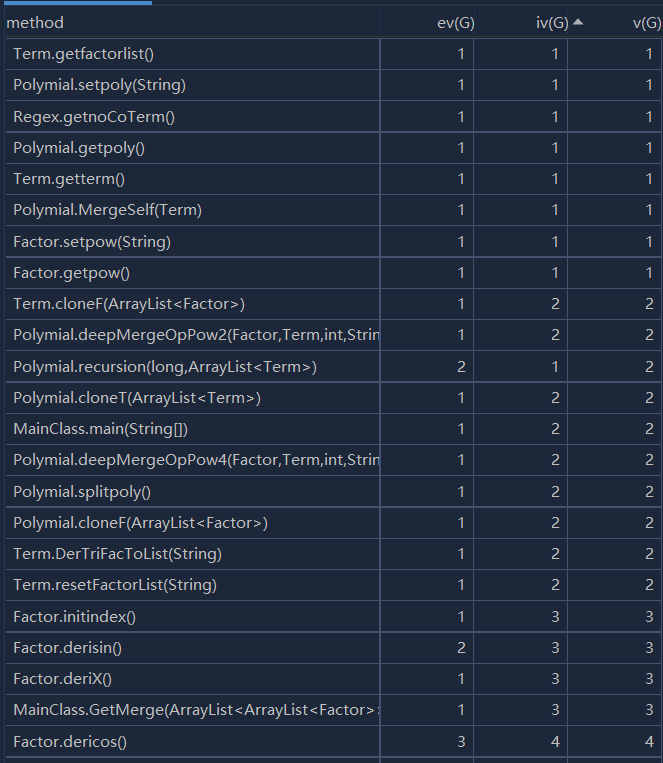
第一次作业
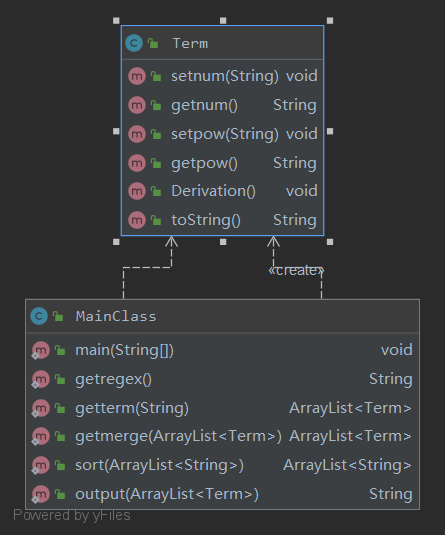
UML图:
度量分析图:
第一次作业虽然较为简单,但本人的复杂度相对而言还是比较高,原因主要在于本人对于面向对象的编程不够熟悉,致使代码颇有面向过程编程的风格。本人的主要思路如下:
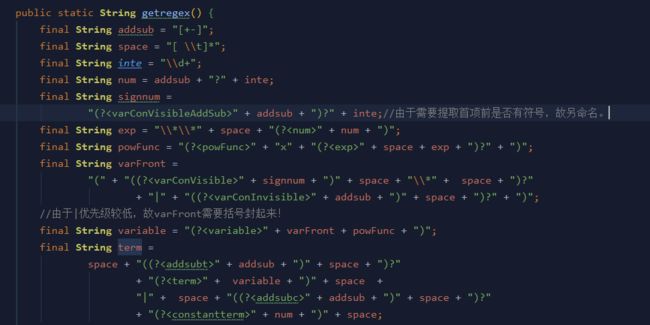
对于输入处理,本人采用的是正则表达式匹配的方式,并用捕获组对幂函数的幂以及系数进行捕获,正则表达式如下:
在对输入数据进行匹配之后,本人新建Term对象将系数和次数进行保存,求导在Term对象内完成。而对于数据的化简,由于第一次作业化简情况比较简单,仅有合并同类项以及一些细节性的化简,在此不予赘述。
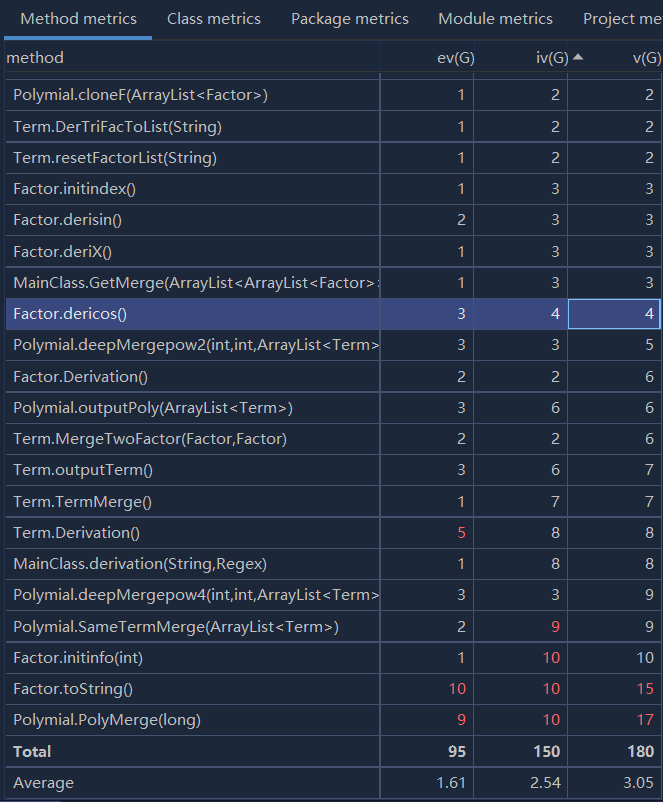
第二次作业
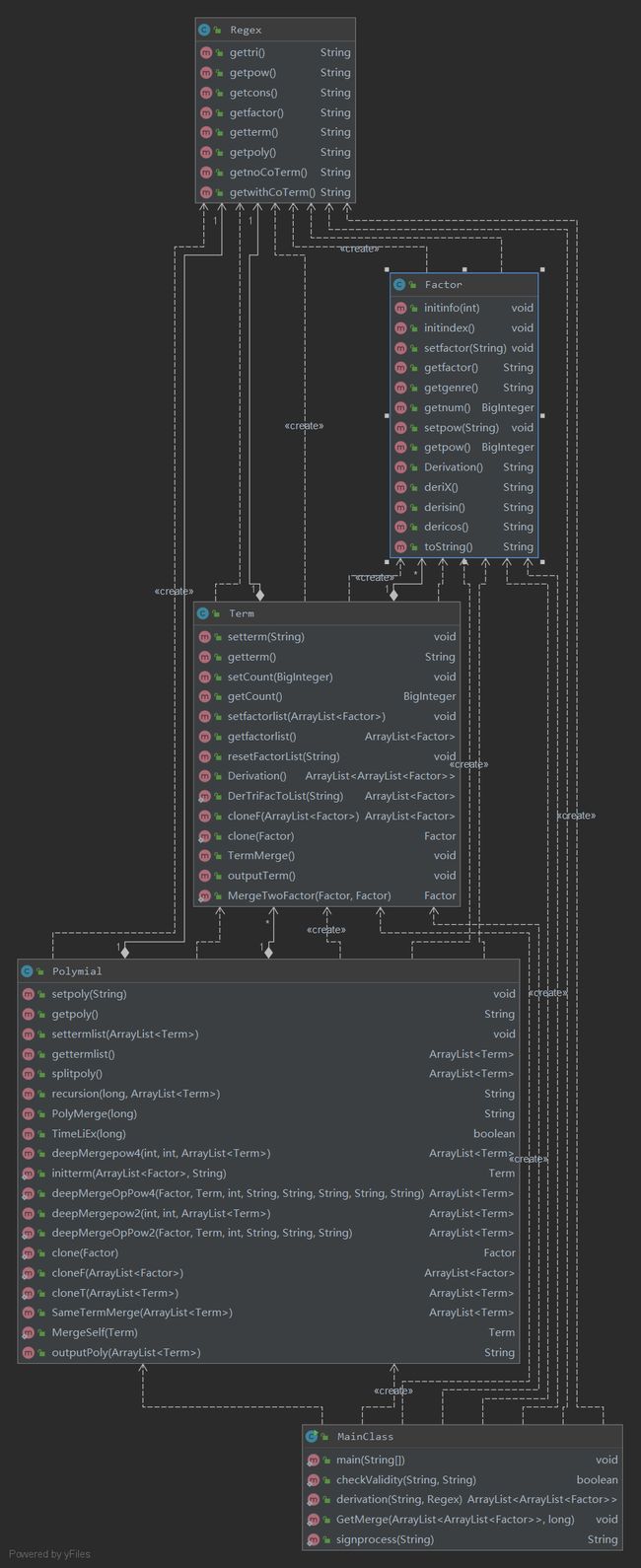
UML图:
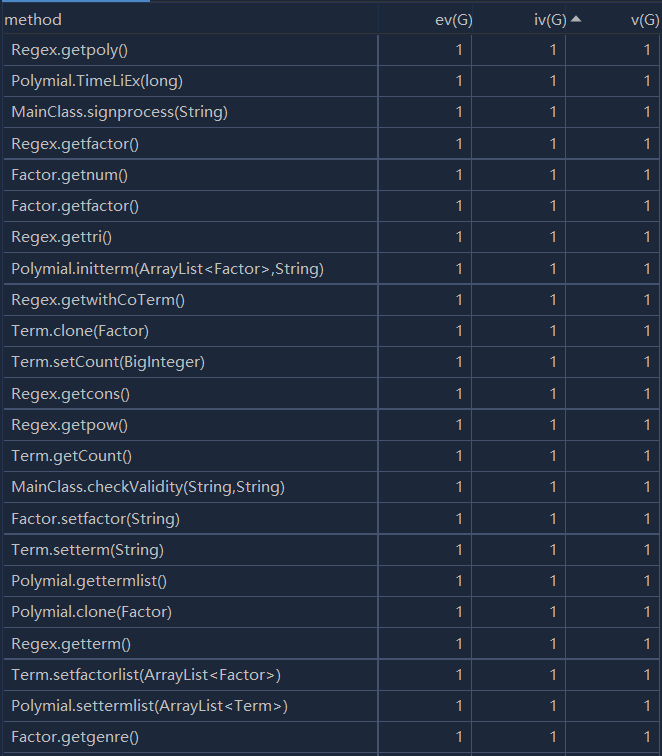
度量分析图:
第二次作业相较于第一次作业添加了连乘项与三角函数求导,本人在第二次作业中进行了重构,将表达式分为了几个不同的层次:Poly,Term,Factor。这样显著降低了本次作业的复杂度,让第二次作业相较于第一次作业而言平均复杂度降低不少。
对于输入的处理同样是使用正则表达式进行匹配:
相较于第一次作业,此次作业进行了空白字符的预处理,正则表达式得到了简化。在解析完毕输入表达式后,新建Polymial,Term,Factor对对应数据进行存储,在Factor与Term类中分别进行因子与项的求导工作。同时,在Polymial类中进行同类相合并,二次三角函数递归化简,四次三角函数递归化简等工作。但由于二次以及四次三角函数的递归化简
运算量巨大,导致此次作业代码在时间性能上表现不佳。
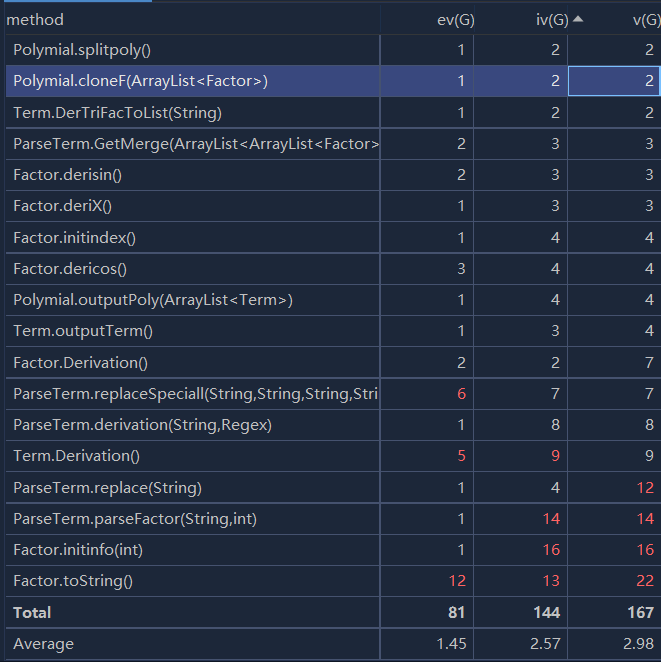
第三次作业
UML图:
度量分析图:
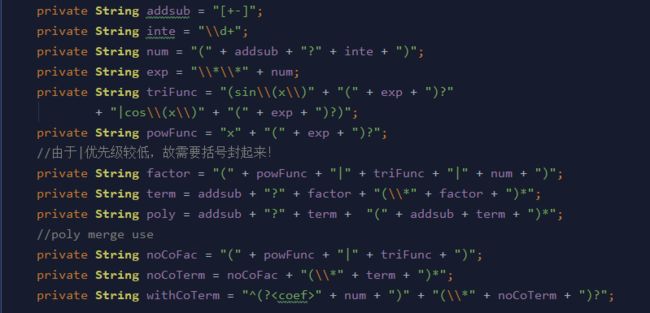
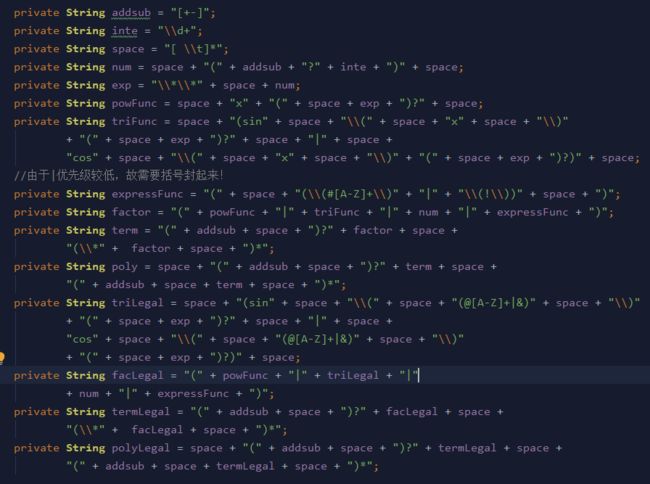
相较于第二次作业,此次作业添加了嵌套规则以及表达式因子。故对此次作业,本人在第二次作业的基础上对输入解析进行了重构。受讨论区J哥方法的启发,使用了递归替换法进行输入表达式的解析与求导,对每一层的三角函数因子与表达式因子进行替换,进入下一层之后继续上述操作直到该层表达式迭代到第二次作业的表达式为止,即可使用第二次作业的求导方法对表达式进行求导,而后递归替换即可。每一层的合法性判断仍然由如下图的正则表达式进行完成。
同时由于第二次作业化简算法复杂度过高,本人在第三次作业中对于化简功能进行了舍弃,以消除第三次作业tle的风险。
二、Bug分析
第一次作业:没有bug。
第二次作业:得到输出表达式之后,使用了replaceAll函数对表达式内的x**2全部替换为了x*x,导致含有类似x**20000的表达式直接错误,将替换函数删除即可解决该问题。
第三次作业:匹配还原方法要求严格保证表达式的顺序,在求导过程中不能有任何化简,否则会打乱替换顺序导致替换出错。本人在求导结果含0的时候将该项进行了省略,导致递归完成后的替换出错,将省略含0项删除即可避免该问题。
本人三次作业中出现的bug基本是由于化简操作出现失误而导致。其中第二次作业的bug甚至导致本人被黑十一刀(虽然最后一行合并修复尽数解决),故在日后的作业中,一定要对优化工作慎之又慎,万不可弄巧成拙。
三、发现别人bug的策略
三次作业均使用自动测评机对其他同学的代码进行自动测试,先是进行一般模式的测试,而后再将评测机生成数据条件修改为生成边界数据再进行测试。同时观察各位同学内的代码是否有一些本人曾经犯过的错误进行详细检查。
四、应用对象创建模式
由于第一二次作业都相对简单,本人采用的是针对每一个对象新建一个类的方法进行对象创建。而在第三次作业当中,由于可以直接使用第二次作业的代码,故本人打消了一开始重构并应用工厂模式的想法。新建一个ParseTerm类对表达式进行解析,其他功能便由第二次作业代码完成即可。(没有尝试使用工厂模式来解决问题实属遗憾。)
四、对比和心得体会
正则表达式实属字符串处理利器,三次作业都通过正则表达式对输入进行了匹配以便于后续处理。但是本人的化简与优化过程从第一次的完全优化,到第二次的舍弃时间性能的优化,到第三次的放弃优化,确实说明自己的优化水平不够,还需提升。(但第三次作业好像优不优化差距不大)最后感谢助教与老师的辛苦工作,也感谢讨论区各位大佬源源不绝地提供各种算法(讲真要是没有大佬们提供算法咱可真不会)。个人提升空间巨大,日后还需加油。