二叉树的三种遍历的应用（表达式，求深度，叶子数，结点数，二叉树的建立，复制）

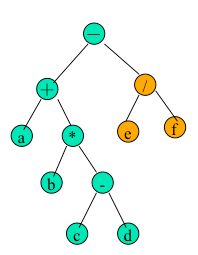
表达式的表示

如图所示的二叉树表达式： a+b*(c-d)-e/f

若先序遍历此二叉树,按访问结点的先后次序将结点排列起来,其先序序列为: (波兰式,前缀表达式)  -+a*b-cd/ef

按中序遍历,其中序序列为：a+b*c-d-e/f (中缀表达式)

按后序遍历,其后序序列为：abcd-*+ef/- (逆波兰式，后缀表达式)

注：人喜欢中缀形式的算术表达式,对于计算机,使用后缀易于求值

查询二叉树中某个结点

使用先序遍历算法进行查询遍历

// 若二叉树中存在和 x 相同的元素，则 p 指向该结点并返回 OK,否则返回 FALSE
bool Preorder (BiTree T, int x, BiNode *p)
{
    //如果二叉树不为空，开始查询结点
    if (T)
    {
        //如果根节点就是目标结点
        if (T->data == x)
        {
            //p 指向该结点并返回真
            p = T;
            
            return true;
        }
        else
        {
            //递归调用，也就是先序遍历
            if (Preorder(T->lchild, x, p))
            {
               return true;
            }
            else
            {
                return(Preorder(T->rchild, x, p)) ;
            }
        }//end of else
    }//end of if
    else
    {
        return false;
    }
}

统计二叉树中叶子结点的个数

还是先序遍历的过程

//统计二叉树中所有末位结点的个数，也就是叶子结点的个数的统计
void CountLeaf(BiTree T, int *count)
{
    //如果不为空树
    if (T != NULL)
    {
        //如果树的左右子树都为空，那么叶子结点数+1
        if ((!T->lchild) && (!T->rchild))
        {
            // 对叶子结点计数
            count++;
        }
        //否则，继续递归遍历
        CountLeaf(T->lchild, count);
        CountLeaf(T->rchild, count);
    } // if
}

统计二叉树中所有结点的个数

//返回指针T所指二叉树中所有结点个数
//还是前序遍历
int Count(BiTree T)
{
    //如果 T 为空
    if (!T)
    {
        //则说明是空树，返回0个结点
        return 0;
    }
    //如果 T 的左右子树 为空，说明只有一个结点，根节点而已
    if (!T->lchild && !T->rchild)
    {
       return 1;
    }
    else{
        //否则，递归遍历
        int m = Count(T->lchild);
        int n = Count(T->rchild);
        
        return (m + n + 1);
    } //else
}

求二叉树的深度(后序遍历)

//求二叉树的深度，后续遍历的使用
int Depth(BiTree T)
{
    int depth;
    int depthLeft;
    int depthRight;
    //如果二叉树为空
    if (!T)
    {
        depth = 0;
    }
    else
    {
        depthLeft = Depth(T->lchild);
        depthRight = Depth(T->rchild);
        depth = 1 + (depthLeft > depthRight ? depthLeft : depthRight);
    }
    
    return depth;
}

复制二叉树(也是后序遍历)，其基本操作为:生成一个结点。

//生成一个二叉树的结点,(其数据域为item,左指针域为lptr,右指针域为rptr)
BiNode * GetTreeNode(int item, BiNode *lptr, BiNode *rptr)
{
    BiTree T;
    //如果新建结点失败
    if (!(T = new BiNode))
    {
        //退出
        exit(1);
    }
    //新建结点成功
    T->data = item;
    //
    T->lchild = lptr;
    T->rchild = rptr;
    //返回新建的结点的指针
    return T;
}

BiNode * CopyTree(BiNode *T)
{
    BiNode *newT;
    BiNode *newlptr;
    BiNode *newrptr;
    //如果源树为空
    if (!T)
    {
        //返回空
       return NULL;
    }
    //如果根的左子树不为空
    if (T->lchild)
    {
        newlptr = CopyTree(T->lchild); //复制左子树
    }
    else
    {
        //左子树为 null
        newlptr = NULL;
    }
    //如果根的右子树不为空
    if (T->rchild)
    {
        newrptr = CopyTree(T->rchild); //复制右子树
    }
    else
    {
        //否则，右子树为 null
        newrptr = NULL;
    }
    //新生成一个二叉树的结点，也就是后续遍历的过程
    newT = GetTreeNode(T->data, newlptr, newrptr);
    
    return newT;
}

建立二叉树的存储结构，以递归方式建立二叉树。

输入结点值的顺序必须对应二叉树结点先序遍历的顺序。并约定以输入序列中不可能出现的值作为空结点的值以结束递归。例如用“@”或用“-1”表示字符序列或正整数序列空结点。

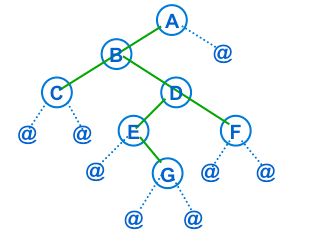
如图所示的二叉树的先序遍历顺序为

A B C @ @ D E @ G @ @ F @ @ @

//递归建立二叉树
bool CreateBiTree(BiTree T)
{
    char ch;
    //输入结点的值
    scanf(&ch);
    //如果输入空字符
    if(ch == ' ')
    {
        //代表空结点
        T = NULL;
    }
    else
    {
        T = (BiNode*)malloc(sizeof(BiNode));
        //如果新建结点失败
        if (!T)
        {
             exit(1);
        }
        //成功。先序遍历的顺序建立二叉树
        T->data = ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
    
    return true;
}

 

欢迎关注

dashuai的博客是终身学习践行者，大厂程序员，且专注于工作经验、学习笔记的分享和日常吐槽，包括但不限于互联网行业，附带分享一些PDF电子书，资料，帮忙内推，欢迎拍砖！