图的生成树（森林）（克鲁斯卡尔Kruskal算法和普里姆Prim算法）、以及并查集的使用

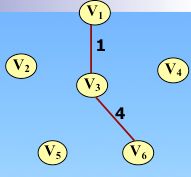
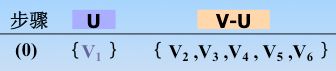图的连通性问题：无向图的连通分量和生成树，所有顶点均由边连接在一起，但不存在回路的图。

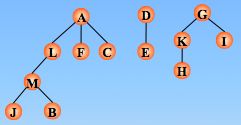
设图 G=(V, E) 是个连通图，当从图任一顶点出发遍历图G 时，将边集 E(G) 分成两个集合 T(G) 和 B(G)。其中 T(G)是遍历图时所经过的边的集合，B(G) 是遍历图时未经过的边的集合。显然，G1(V, T) 是图 G 的极小连通子图，即子图G1 是连通图 G 的生成树。

深度优先生成森林

  右边的是深度优先生成森林：

连通图的生成树不一定是唯一的， 不同的遍历图的方法得到不同的生成树;从不同的顶点出发可得到不同的生成树。

连通图本身就是连通分量，其中顶点集+遍历经过的边=生成树。

非连通图的生成森林不一定是唯一的。

非连通图各个连通分量的顶点集+遍历时经过的边=若干颗生成树（生成森林）

最小生成树 
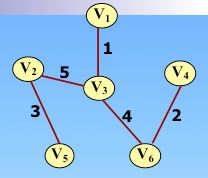
给定一个无向网络，在该网的所有生成树中，使得各边权数之和最小的那棵生成树称为该网的最小生成树。

问题的提出：要在 n 个城市间建立交通网，要考虑的问题如何在保证 n 点连通的前题下最节省经费? 

如何求连通图的最小生成树?

构造最小生成树的算法很多，其中多数算法都利用了一种称之为 MST 的性质。

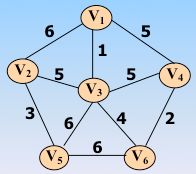
MST 性质：设 N = (V, E)  是一个连通网，U 是顶点集 V 的一个非空子集。若边 (u, v) 是一条具有最小权值的边，其中u∈U，v∈V-U，则必存在一棵包含边 (u, v) 的最小生成树。

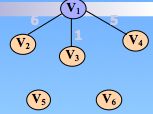
方法一：普里姆 (Prim) 算法。

算法思想：

1、设 N=(V, E) 是连通网，TE 是N 上最小生成树中边的集合。初始令 U={u0}, (u0属于V ), TE={ }。

2、在所有 u属于U, v属于V-U 的边 (u, v)属于E 中，

找一条代价最小的边 (u0, v0)。

将 (u0, v0) 并入集合 TE，同时 v0 并入 U。

 

3、

重复上述操作直至 U=V 为止，则 T=(V, TE) 为 N 的最

小生成树。

 

总得来说，普里姆算法就是以树为单位，找最小的权边，特点是针对无向图！只和顶点有关，和边无关，适用于稠密图。算法时间复杂度为 O（n^2）

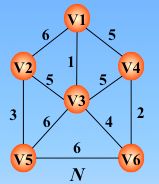
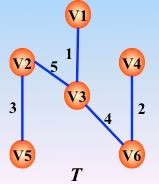
如图：普里姆算法求最小生成树

初始令 U={u0}, (u0属于V ), TE={ }。

   

在所有 u属于U, v属于V-U 的边 (u, v)属于E 中，找一条代价最小的边 (u0, v0)。将 (u0, v0) 并入集合 TE，同时 v0 并入 U。

   

重复上述操作直至 U=V 为止，则 T=(V, TE) 为 N 的最 小生成树。

    

继续

    

最后，遍历完

    

Prim算法的实现  

顶点集合如何表示？最小边如何选择？一个顶点加入U集合如何表示？如下面的例子：

当U集合中加入一个新顶点时，V-U集合中的顶点到U的最小代价边可能会更新，k 代表最终选择的顶点，k=3，代表选择是v3这个顶点，因为1-3代价是最小的=1

选取了 v3，之后，继续以最新的树为单位，来找最小的权值边，通过看和哪个顶点连接。

k=6，代表选择是v6这个顶点，因为3-6代价是最小的=4，在所有的和最新的树邻接的顶点中，权值最小的边。

选取 v6之后

继续以最新的树为单位，找临近的顶点，看哪条边的权值最小，找到6-4这条边，权值=2

新的树如图

继续以最新的树为单位，找临近的顶点，看哪条边的权值最小，找到3-2这条边，权值=5

新的树如图

继续以最新的树为单位，找临近的顶点，看哪条边的权值最小，找到2-5这条边，权值=3

直到所有顶点全部并入生成树之后，程序结束

 

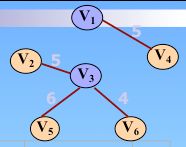
方法二：克鲁斯卡尔 (Kruskal) 算法。

使用了并查集，直接从边中找到不成环的最小的权边（最简单的求最小生成树的算法），特点：只针对无向图，包好普里姆算法，都是只针对无向图。

算法思想：

1、设连通网  N = (V, E )，令最小生成树初始状态为只有 n 个顶点而无边的非连通图 T=(V, { })，每个顶点自成一个连通分量。

2、 在 E 中选取代价最小的边，若该边依附 的顶点落在 T 中不同的连通分量上（即： 不能形成环），则将此边加入到 T 中；否 则，舍去此边，选取下一条代价最小的边。

3、依此类推，直至 T 中所有顶点都在同一连通分量上为止。

最小生成树可能不惟一（包括普里姆算法都是一样的道理）

把所有的边按照权值升序排列，从最小边开始（不能形成回路），选取，组成最小生成树。直到所有的边并入则结束（不是顶点！） 克鲁斯卡尔算法主要在排序边的权值序列的时候最费时间，他的算法时间复杂度和排序算法有关，而排序算法的时间复杂度和图的边 e 有关系，和顶点 v 没有关系。故适用于稀疏图。（而普里姆算法适合稠密图）

下面是图解步骤：

按照升序，找出权值的排序序列：1 2 3 4 5 5 5 6 6 6

注意选取权值最小的边的时候，不要形成回路

按照权值的升序排列的顺序查找选取合适的边

继续，按照权值的升序排列的顺序查找选取合适的边

注意选取5的时候，避免环的生成，即可

直到所有的边都并入即可。

那么在克鲁斯卡尔算法里，通过找合适的边，该如何避免形成回路呢？换句话说，如何判断是否形成了回路？

使用并查集可以判断是否形成了回路，kruskal算法用到了一种贪心策略，首先要把边集数组以边的权值从小到大排序，然后一条边一条边的查找，如果边的两个端点不在一个集合内，则将此边添加到正在生长的树林中，并合并两个端点所在的集合，直到最小生成树已生成完毕。

并查集：

是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。集就是让每个元素构成一个单元素的集合，也就是按一定顺序将属于同一组的元素所在的集合合并。

并查集是一种非常简单的数据结构，它主要涉及两个基本操作，分别为：

A． 合并两个不相交集合

B． 判断两个元素是否属于同一个集合

1）合并两个不相交集合（Union(x,y)）

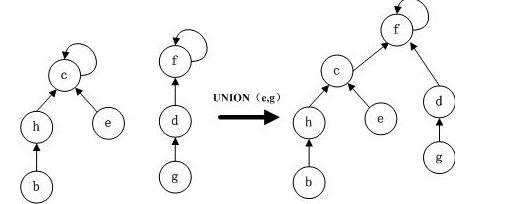
合并操作很简单：先设置一个数组Father[x]，在克鲁斯卡尔算法里，需要使用双亲存储结构，表示x的“父亲”的编号。那么，合并两个不相交集合的方法就是，找到其中一个集合最父亲的父亲（也就是最久远的祖先），将另外一个集合的最久远的祖先的父亲指向它。

通俗的说，就是把其中一个树的根，作为另一个树的根结点的一个孩子结点即可。

上图为两个不相交集合，合并后可以看出：Father(b)=Father(g)=f 结点

2）判断两个元素是否属于同一集合（Find_Set(x)），本操作可转换为寻找两个元素的最久远祖先是否相同。可以采用递归实现。

并查集的优化问题

寻找祖先时，我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次Find_Set(x)都是O(n)的复杂度。为了避免这种情况，我们需对路径进行压缩，即当我们经过”递推”找到祖先节点后，”回溯”的时候顺便将它的子孙节点都直接指向祖先，这样以后再次Find_Set(x)时复杂度就变成O(1)了，如下图所示。可见，路径压缩方便了以后的查找。

回到克鲁斯卡尔算法，使用并查集来实现判断回路的生成否

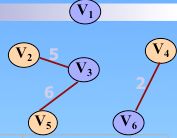
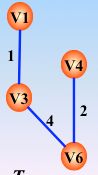
比如从 v1开始（一共是 v1、v2、v3、v4、v5、v6），则开始把 v1-v6作为各个单根树，以森林来表示，让每个元素构成一个个的单元素的集合，需要使用数组表示，存储方式就是双亲存储结构（方便找到共同的父亲）。

每次使用并查集，将后入的边上的另一个结点作为孩子结点，而没有加入的结点还是去做为单根的树：

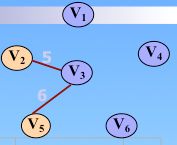
如图所示，上图，该选取权值=5的边了，此时有两个树

   和   

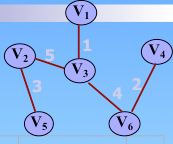
如果选取3-4或者1-4这两条边的任意一个，单根树是不会产生根相同的情形的，而加入的（作为孩子的根），一定会找到共同祖先的，这样就可以发现回路的存在！ 而选取2-3这条边的话，在并查集中，就不会查出共同的祖先，也就是没有环的形成。

通俗的说，就是通过两个元素所在的结点推出跟结点，若根相同，则为同一个集合，否则不是同一个集合（也就是不形成回路）

 

欢迎关注

 

dashuai的博客是终身学习践行者，大厂程序员，且专注于工作经验、学习笔记的分享和日常吐槽，包括但不限于互联网行业，附带分享一些PDF电子书，资料，帮忙内推，欢迎拍砖！