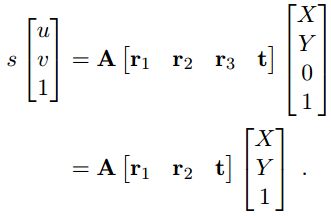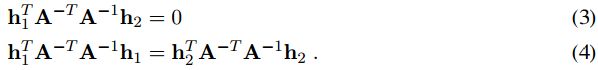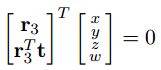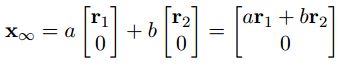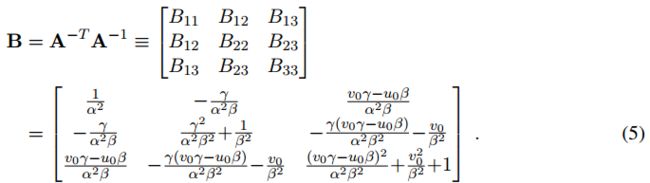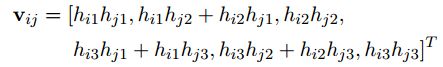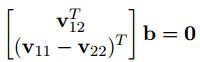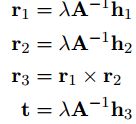我发现认识的大佬都有写博客的习惯,今天我建立了这个文集,从现在开始我也开始对机器视觉及相关领域的学习过程做一些笔记和整理,同时记下自己的心得体会,作为记录,同时也分享给大家。
本文按照张正友的原文顺序,进行一些解读或笔记记录。
第一部分:相机标定的动机
相机标定在3D视觉中是非常重要的一个步骤,因为我们要从一些2D图像中获取待测物的3D信息。目前的相机标定方法大致可以分为两大类:
① 摄影测量标定:此类方法一般需要通过观察三维尺寸已知且精度非常高的待测物来实现,一般情况下该方法的待测物包含了两个或三个相互正交的平面,有时候平面还需要进行精度较高的变换。这类方法标定效率高,但成本也高。
② 相机自检校标定法:这类方法不需要任何标定物,只需要调整相机,从不同角度取拍摄某静态画面,此画面一般能提供2个相机内参解析的约束条件。如果相机内参不变,那么三幅画面就可以让我们同时解得相机内参和用于3D重构的外参。这类方法非常灵活,但是不够成熟。
第二部分:基本方程
2.1 相机针孔模型回顾
在另一篇文章中我会对针孔模型进行详细的讲解,这里只作简要回顾。针孔模型链接:
根据相机针孔原理,可以推导出空间3D点M的坐标和它的像素坐标之间的关系如下所示
(1)
式中:,表示像素坐标系下的坐标;,表示世界坐标系下的坐标;s为尺度因子;R为世界坐标系与图像坐标系的旋转矩阵,t为世界坐标系与图像坐标系的平移向量,R和t中的参数均被称为相机的外部参数,简称外参;矩阵A被称为内参矩阵,如下所示:
矩阵A中,为光轴与像平面焦点在像素坐标系下的坐标,将它成为主点;α和β是图像u轴和v轴上的尺度因子,γ为像素两轴非正交项。
2.2 模型平面和像面之间的单应性矩阵 Homography
OK,单应性什么意思呢?这里对单应性做一丢丢的解释:Homography其实就是一个变换(3*3矩阵),目的是将一张图中的点映射到另一张图中对应的点,单应性变换是对齐次坐标下点的线性变换,单应性矩阵约束强,是点到点的一一对应。
假设待测平面是在世界坐标系Z=0处,那么通过(1)式可以得到:
因此可以得到,世界坐标系(Z=0)平面下的点M及其在像平面中的像坐标关系可以用如下的单应性矩阵H联系起来:
其中, (2)
2.3 相机内参约束条件
若给定模型平面(即世界坐标系下Z=0的平面)下的一幅图像,那么对应的单应性矩阵就可以被写出来,将该单应性矩阵设为,从(2)式可以得到:
其中λ为任意实数。(为什么这里λ可以为任意实数?主要是因为齐次坐标有规模不变性。这就要从齐次坐标讲起了,后面我会写一篇专门说说其次坐标和欧氏空间的关系)
由于旋转矩阵的三个向量具有空间正交特性,且任意一行或一列对应的向量模都为1,因此可以得到:,,而(此处令λ=1),因此可以得到下式:
上述两个式子即为给定一个单应性矩阵,针对相机内参的两个约束条件。由于一个单应性矩阵包含了8个变量(由于齐次坐标的规模不变性,可以任意设置(2)中尺度参数,那么矩阵H中的参数可以由9个变为8个),并且待求的外部参数一共有6个(3个旋转和三个平移),因此我们只能得到2个内参的约束条件。
2.4 几何解释
先请移步看一下这一小节的基础:绝对圆锥曲线~~
模型平面在相机坐标系下可以写为(这里还没明白,请各路大神明白了帮忙补充~):
当w=0时,表示无穷远处的点;w=1时与之相反。此平面与无穷远处的平面相交为一条线。由于//相互正交,因此,,又因为无穷远处w=0,因此可以很容易看出点和都在这条无穷远处的相交线上。并且任意一个在该线上的点都可以用这两个点的线性组合来表示,如下:
接下来计算绝对圆锥曲线和该交线的交点,根据定义,无穷远处绝对圆锥曲线上的点满足:,即,则b=±ai,那么交线与绝对圆锥曲线的交点为:
这两个点的像点为:
由于无穷远交线是在相机坐标系下表示的,个人理解该交线是以相机主点为圆心的弧线,因此无穷远处的点在像平面上的投影只与相机内参(含尺度因子,只不过由于齐次坐标,尺度因子的值不影响结果)有关,旋转矩阵为单位矩阵,即不发生旋转,,,而平面在世界坐标系Z=0处,根据(2)式,没有对世界坐标起作用,因此可以省略,那么(2)可以写为:
并且已经知道,因此:
展开后为:
这个式子中的实部和虚部都必须为0,因此可以得到(3)和(4)式。(why只有一组,不应该还有一组么....有谁明白的帮忙解释一下......)
3 解决相机标定问题
这一小节主要详细讲解如何实现对相机的标定。
3.1 闭合解
令:
矩阵B是对称矩阵,其中有6个参数:
假设H的第i列为:,那么可以得到:
其中:
【这个过程可以用maple去验证~】
再把前文的2个约束条件拿出来看一下:
那么这两个式子可以简洁地写为:
若我们有n幅图像,那么一共就有2n个方程。
如果n=1,就只能得到2个方程,此时只能假设主点坐标已知,且γ=0,来求解α和β;如果n=2,那么就能得到4个方程,但是相机内参A中有5个参数,此时可以令γ=0,从而求解其他四个主要参数;如果n≥3,我们就可以解得b中的所有参数。
一旦b确定下来,就能够解得矩阵A中的所有相机内参。
A已知后,每幅图像的外参也就能同时确定下来。
其中:
3.2 最大似然估计
假设我们获取了n幅标定板图像,每个图像上有m个点,那么可以获取下式的极小值得到最大似然估计:
其中,为点在第i幅图像的投影点。
首先要获得A的估计值,然后利用上面的描述的求解方法,获得,,然后利用LM迭代优化方法,使得上式最小化。
3.3 径向畸变
假设理想状态下,像素坐标为(u,v),对应的实际坐标为,理想状态下的坐标为相机针孔模型得到的坐标。其对应的图像坐标为(x,y)和。那么根据畸变:
将(令γ=0)和带入可以得到:
对于每个图像上的每个点,可以写为:
在已经估计出A中的参数后,我们可以获得理性情况下的坐标(u,v),然后我们就可以用上式来估计畸变参数k1和k2。
如果有n幅图像,每幅图像上有m个点,那么总共能获得2mn个方程:
其中D为2mn*2的矩阵。。其最小二乘解为:
当畸变参数估计完成后,我们就可以将非线性优化调整为:
标定流程:
1 打印出一张标定图并贴到一个平面上; 2 通过移动相机或者标定平面采集不同位置、不同方向的标定板图像;3 特征点检测;4 估算内参,然后得到外参;5 估算畸变系数;6 优化所有参数。
Matlab有自带的CameraCalibration标定工具箱,可以直接用,很方便。
本文有很多内容都是基于本人的理解,若理解有误,欢迎指正!
原文出处:A flexible new technique for camera calibration - IEEE Journals & Magazine