题目链接http://acm.hdu.edu.cn/showproblem.php?pid=5963
吐槽
这道题我第一眼看,嗯??博弈论?还是树上的?我好像不会啊。。。但是一想某人的话,感觉这个应该也不会太难,可能有规律
分析
于是我就从样例开始仔细思考找规律,第一个样例应该是看不出来啥,但第二个内容量就比较丰富了。但我模拟完样例二依旧没发现什么,难道这道题真要建个线段树什么的??接着我把关注点放到了输出上,输出只有两种,那是不是应该存在某种奇偶关系?还是要先考虑链的情况,因为从无根树上的一个点出发遍历就相当于走几条链(好像树的问题大部分都跟链有关)。下面模拟一下

首先要注意到题目中的暗示,每次都要找一个到父亲节点权值为1的点,这就说明了这个问题的限制,它总会结束。先不考虑修改,如果以1为根,不难看出女孩会赢,其中一种走法是
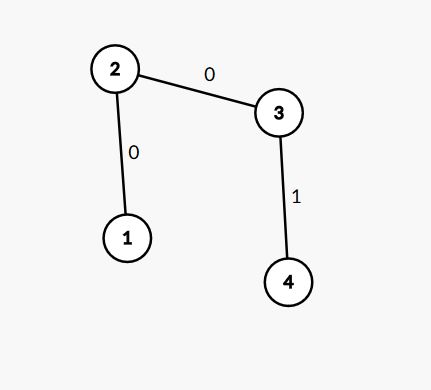

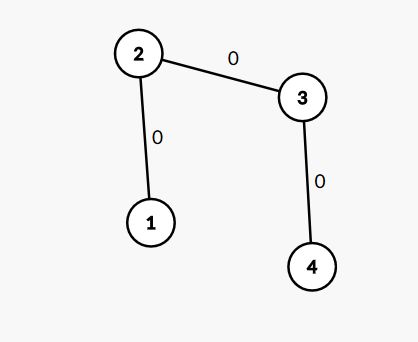
当然也有别的走法,但总会是女生赢。
如果以2为根呢?不难得出还是女孩赢,其中一种走法为

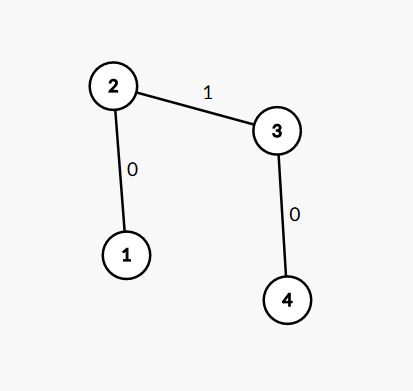

那么是不是图中边权为1的边数为偶数时,就是女生赢呢?仍旧以2为根,我们在4后边再跟一个节点。
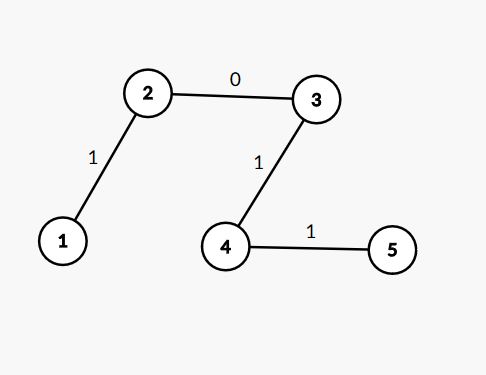
会发现这样还是女生赢。
那在根节点2后边跟这个节点呢?

这时候再去模拟就会发现是男生赢了。所以我们猜测,让女生赢的并不是图中边权为1的边数,而是根节点周围边权为1的边数,根据这个大胆的猜测,我写出了下面的代码,好像还白写了一个加边函数。如果你去用样例测试,发现是对的,所以我兴奋的交了上去,WA
#include
#include
using namespace std;
const int N=4e4+10;
struct Edge{
int to,nxt,val;
}e[N<<1];
int Head[N],len;
void Ins(int a,int b,int c){
e[++len].to=b;e[len].val=c;
e[len].nxt=Head[a];Head[a]=len;
}
int cnt[N];
int main(){
int t;
scanf("%d",&t);
while(t--){
int n,m;
scanf("%d%d",&n,&m);
memset(cnt,0,sizeof(cnt));
for(int i=1;i 二次分析
既然这个代码过了样例,就说明它应该不是偶然,所以应该是我少考虑了什么。再回去读了一边题,发现题中并没有说当\(op==1\)时,变换的权值与原来的权值相等,也就是说如果我每次都把1变为0,0变为1,那么我上边的代码是可以的,也就是样例情况,但问题就出在它可能是1变为1,0变为0,所以每次必须扫描一边根周围的边权之和,即下边的代码。
#include
#include
using namespace std;
const int N=4e4+10;
struct Edge{
int to,nxt,val;
}e[N<<1];
int Head[N],len;
void Ins(int a,int b,int c){
e[++len].to=b;e[len].val=c;
e[len].nxt=Head[a];Head[a]=len;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
int n,m;
scanf("%d%d",&n,&m);
memset(Head,0,sizeof(Head));
len=0;
for(int i=1;i 证明
写完之后感觉就这么过去的话不是很好,万一猜错了就很尴尬,所以想一下证明。
为了简化问题,我们只把链的情况证明了就好。如果连接根节点的边权值为1,其余边有两种情况,一是全为1的,二是含0的,分开讨论一下。
如果含有0,
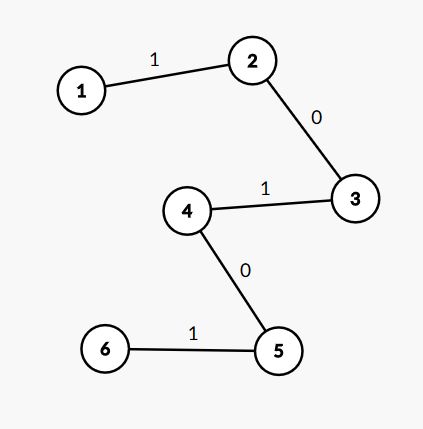
因为是女生先任意选点,所以让女生选择最后一个点,这样连接根节点的那条边就会被置为0,而因为含有0,所以肯定还会剩下边权为1的,这时由于男生不得不去变换边,所以一定会去变换权值为1的,由于根节点在男生变换的时候为0,所以这样的话只有可能是女生让根节点变为0,也就是只有女生会赢。
如果不含0都是1呢?那女生就可以一次性让男生没的变换,仍然是女生赢。
当连接根节点的边权值为0时就会反过来,证毕。